35 Maths Questions Year 6: SATs Reasoning Questions And Answers With Worked Examples
Maths questions in Year 6 assess pupils’ ability to apply their knowledge of key maths topics from KS2 to new and unexpected contexts. Year 6 maths questions are designed to move past knowledge recall, instead requiring pupils to demonstrate problem solving skills, critical thinking and reasoning.
This comprehensive collection of maths questions for Year 6 is designed by Third Space Learning’s expert team of teachers. All questions include answers and are organised by question type to familiarise pupils with the most common question types they are likely to encounter in the KS2 SATs.
SATS 2026: STAY UP TO DATE
Join our email list to stay up to date with the latest news and free resources for SATs 2026. As usual our expert teachers will be on hand to provide one to one tuition support, revision resources, expert paper analysis, SATs teacher survey results and the SATs results 2026.
Key takeaways
- Key Stage 2 reasoning papers are often a challenge for Year 6 pupils, even for classes with strong subject knowledge.
- Expose pupils to all 7 question types to build familiarity with different SATs formats.
- Ensure pupils master the vocabulary so they can accurately decode exactly what a question is asking them to do.
- Train pupils to identify multi-step problems so they can break down calculations and complete them in the right order.
- Encourage pupils to show their working out to ensure they pick up method marks even if the final answer is wrong.
- Teach pupils to explain their logic using mathematical rules to prove why a specific answer is correct.
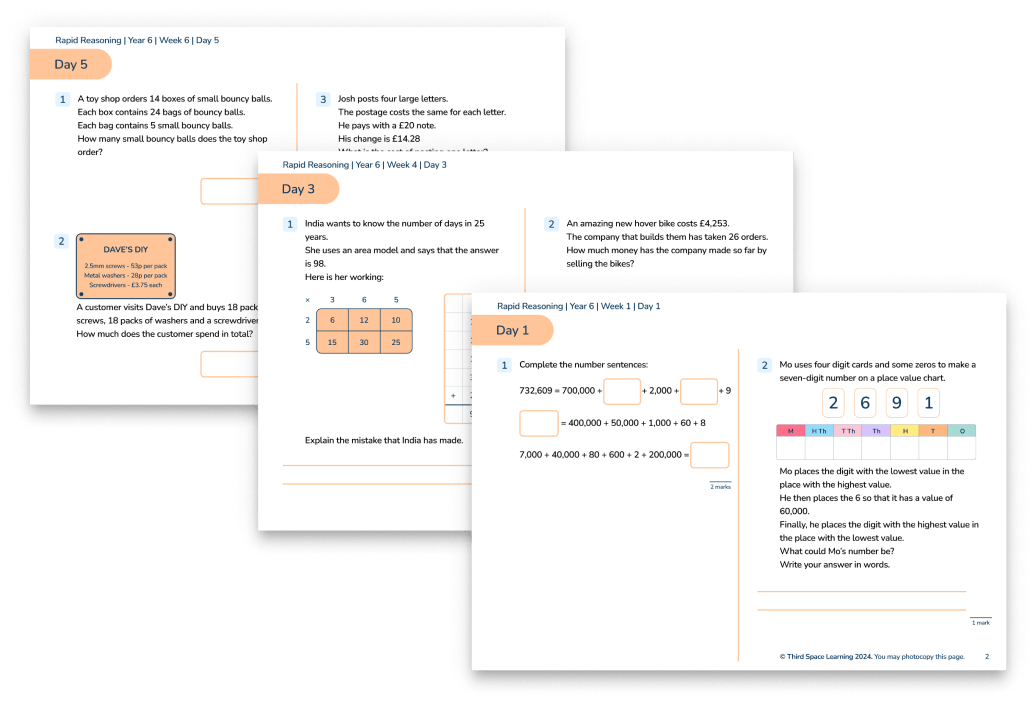
Year 6 Rapid Reasoning (Weeks 1-6)
Download 6 weeks of Rapid Reasoning slides for your Year 6 pupils and help them get a head start on preparing for the SATs reasoning papers.
Download Free Now!More free SATs questions (including answers):
- 75 KS2 SATs maths questions Reasoning and Arithmetic practice questions by topic – includes fractions, decimals, percentages; place value; addition and subtraction.
- 250+ SATs questions
- Year 6 algebra questions
- Year 6 arithmetic questions
- Year 6 ratio questions
- Year 6 fractions questions
- Free year 6 maths test
35 SATs maths questions for KS2 Year 6 SATs
Drawing on over 10 years’ experience preparing Year 6 pupils for the KS2 SATs through one to one SATs tutoring and teaching resources, this list prepared by Third Space Learning’s expert teachers provides you with a sample of the different types of KS2 SATs reasoning questions. The questions cover all major content areas from the KS2 maths curriculum:
- Number and Place Value
- Addition and Subtraction, Multiplication and Division (The Four Operations)
- Fractions KS2
- Decimals and Percentages KS2
- Ratio KS2 and Proportion
- Algebra KS2
- Measurement
- Geometry KS2
There are seven types of maths reasoning questions likely to appear in the Year 6 SATs:
- Single step worded problems
- Multiple step worded problems
- Problems involving measures
- Problems involving drawing
- Explanation questions
- Sequence questions
- Ordering questions
For each of these 7 question types, we’ll:
- Provide further examples taken from Third Space Learning’s Rapid Reasoning resource with worked examples and an explanation for each.
- Examine an example from a previous SATs paper: looking at the question, the correct answer, and advice on how to approach it.
Single step word problems
The simplest type of reasoning question Year 6 pupils are likely to encounter in the reasoning papers: single step problems. Single step problems ask pupils to interpret a written question and carry out a single mathematical step to solve it.
Have a look at the question below:
Question 1: Money and place value

Question: The cheese costs £1.35. Amina pays with a £2 coin.
How much change should Amina get?
Answer: 65p
A relatively easy question to interpret and solve in two steps:
- Recognise that £2 and £1.35 are equivalent to 200 and 135.
- Subtract 200 from 135.
The most crucial skill for primary school pupils in this question is a solid understanding of money as relating to place value. If this understanding is present, the mathematical step itself is quite easy.
Below are several more examples, taken from Third Space Learning’s Rapid Reasoning resources:
Question 2: Time conversions
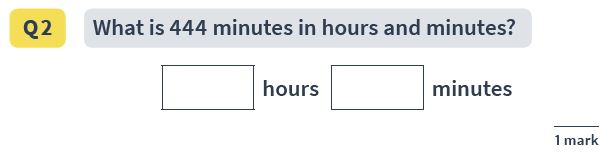
Question: What is 444 minutes in hours and minutes?
Answer: 7 hours 24 minutes
Pupils need to understand that one hour is equal to 60 minutes. From here the single mathematical step is short division: 444/60, with a remainder.
Question 3: Volume of cuboids

Question: A cuboid has side lengths of 4cm, 3cm and 4cm. What is the volume of the cuboid?
Answer: 48 cm3
Pupils must calculate length by breadth by height, using the figures provided by the question.
Question 4: Circle geometry (radius and diameter)

Question: A car wheel has a radius of 62cm.
What is the diameter of the wheel?
Answer: 124 cm
A simple enough calculation (doubling) if pupils are aware that the diameter is twice the radius.
Question 5: Rounding numbers

Question: Round 7,594 to the nearest ten.
Answer: 7,590
A single, relatively simple rounding problem – pupils should recognise that ’94’ is the operative part of this figure.
READ MORE: Rounding numbers
Multi-step worded problems
Multi-step problems require Year 6 pupils to interpret a written problem, but solving it then requires the use of two or three maths skills.
For example, consider this question from the 2019 KS2 maths SATs:
Question 6: Four operations with fractions and money
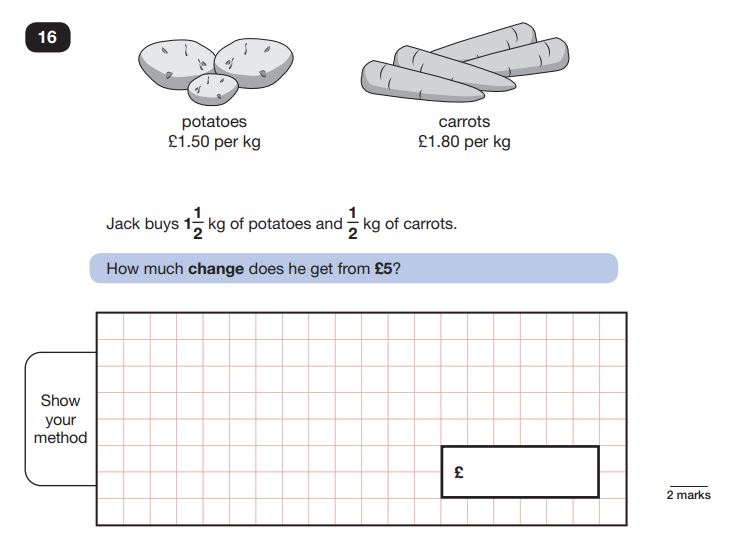
Question: Potatoes cost £1.50 per kg. Carrots cost £1.80 per kg.
Jack buys 1\frac{1}{2} kg of potatoes and \frac{1}{2} kg of carrots.
How much change does he get from £5?
Answer: £1.85
This question encompasses three different maths skills: multiplying (and dividing) mixed numbers, addition and subtraction. Pupils can choose to work out the multiplication or division first, but must complete both before moving on.
Once these values have been worked out the next steps are relatively simple:
- Add the two values together.
- Subtract the total from £5.
Multi-step problems require children to apply their knowledge of maths language and their reasoning skills several times across the course of a single question, usually in slightly different contexts.
More examples:
Question 7: Multi-step multiplication

Question: Wishy Washes car wash processes 92 cars per day. They make £15 per car.
How much money will they have made in 4 days?
Answer: £5,520
There are two steps to this problem, but both are multiplications:
- Multiply this sum by 4 – the number of days – to get to the solution.
- Work out how much money is made per day – 92 x £15.
Question 8: Percentages of amounts

Question: An aeroplane is flying from Birmingham to New York. The distance between these two cities is 5,400 km.
On the journey, the pilot announces, “We are 40% of the way through the flight.”
How far has the aeroplane travelled?
Answer: 2,160 km
Another two step problem:
- Multiply this by 4 to solve 40%.
- Work out 10% of 5400 km.
Question 9: Mean average and multi-step money

Question: Gracie buys 2 adult tickets and 2 child tickets for the theme park. Adult tickets cost £51 each. Children’s tickets cost £36 each.
What was the mean cost of the tickets?
Answer: £43.50
There are three steps involved in solving this problem:
- Multiplication: Double £51 and £36 to find the cost of two adult and two child tickets.
- Addition: Put the two costs together.
- Division: Divide the total by four to obtain the mean cost.
Given the number of steps involved it can be easy for pupils to make arithmetic mistakes, and the mark scheme accounts for this by allowing for one mistake – but no more.
READ MORE: Mean, median, mode
Question 10: Decimals and multi-step mass
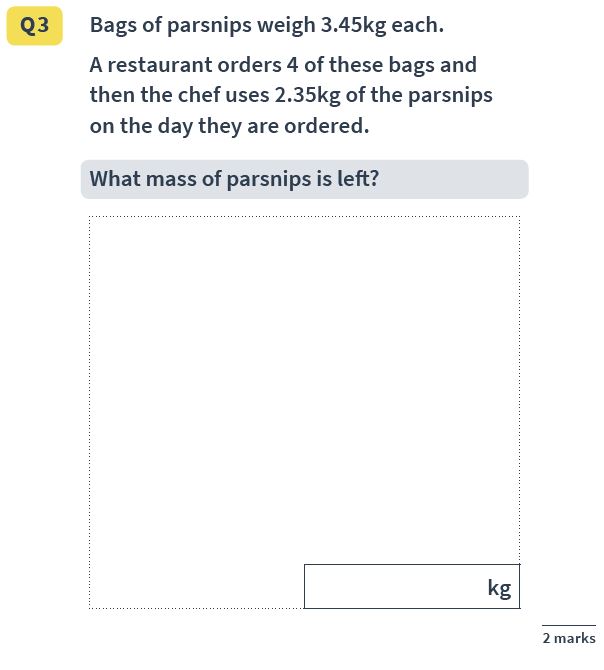
Question: Bags of parsnips weigh 3.45 kg each. A restaurant orders 4 of these bags and then the chef uses 2.35 kg of the parsnips on the day they are ordered.
What mass of parsnips is left?
Answer: 11.45 kg
A two-step problem again:
- Multiply 3.45 kg by 4.
- Subtract 2.35 kg from the total.
As with the previous problem, the mark scheme again allows for at most one arithmetic error, assuming the method is correct.
Problems involving measures
These questions ask pupils to solve a problem that includes one or more units of measurement.
Take a look at this question from 2018’s Reasoning Paper 3:
Question 11: Converting units (kg to g) and division
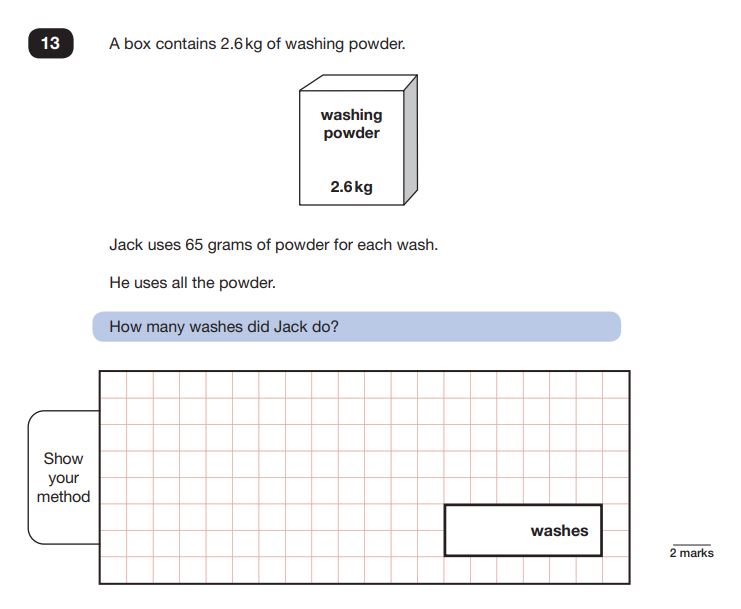
Question: A box contains 2.6 kg of washing powder. Jack uses 65 grams of powder for each wash. He uses all the powder.
How many washes did Jack do?
Answer: 40 washes
This is a two step problem:
- Pupils must first be able to read and convert kilograms to grams (and therefore know the relationship between the two units).
- Divide 2600 by 65 to work out the number of washes possible.
Measure questions are usually limited in the KS2 exam, however they are often used to test core skills like the four operations.
Further examples:
Question 12: Fractions of mass

Question: Pasta has 250 g of carbohydrate per kilogram. There are 200 g of pasta in each small packet.
How much carbohydrate is in each small packet?
Answer: 50g
A relatively simple division problem, relying on pupils having knowledge that 200g is one fifth of a kilogram.
Question 13: Multi-step mass calculation

Question: Four melons have a mean mass of 500 grams. The largest melon is removed. The mean mass of the remaining three melons is 300 grams.
What was the mass of the largest melon?
Answer: 1.1kg
Another three step problem:
- Multiply 500 by 4 to get the total mass of the four melons.
- Multiplying 300 by 3 to get the total mass of the remaining three melons.
- Subtract 900 from 2000 to obtain the mass of the fourth melon.
The mark scheme allows either 1.1kg or 1,100g as acceptable answers – the units of measurement are not as important as obtaining the current figure.
Question 14: Unit precision (cm vs m)

Question: A stack of 40 identical boxes is 240 cm tall. Mia takes four boxes off the top.
How tall is the stack now?
Answer: 216 cm
In this problem, the units for the answer are specified and an answer given in metres will be marked as wrong as cm is specified in the answer box. This is why it’s important to encourage pupils to check whether units are provided in the answer box.
Question 15: Arithmetic mean and missing values in mass

Question: Four toy cars have a mean mass of 80 grams. The heaviest car is removed. The mean mass of the remaining three cars is 50 grams.
What was the mass of the heaviest car?
Answer: 170 g
As with the melon question, there are three steps involved to solve this problem:
Subtract 150 from 320 to get the mass of the fourth car.
Work out the mass of the four cars (4 x 80).
Work out the mass of the remaining three cars (3 x 50).
Problems involving drawing
Problems involving drawing require pupils to construct an accurate drawing by following a set of instructions, or through reflection, translation, or scaling.
This type of question is quite rare, but there are some notable exceptions, such as the infamous Question 21 in Paper 2 of the 2019 Reasoning SATs:
Question 16: Area, square numbers, and geometry

Question: Adam has a rectangular piece of card (pictured). It is marked with grid lines.
Adam makes two straight cuts along the grid lines. The two cuts divide the rectangle into 3 shapes:
- 2 squares of different size, and
- 1 rectangle.
Using the grid lines, draw two lines that show where Adam could have made his cuts.
Use a ruler.
Answer: Any pair of lines that make a square of 4 units, a rectangle of 6 units, and a square of 25 units.
This question is considerably more complex than it appears, and incorporates aspects of multiplication as well as shapes and spatial awareness. One potential solution is to work out the area of the card (35), then work out the possible square numbers that will fit in (understanding that square numbers produce a square when drawn out as on a grid), and which then leave a single rectangle behind.
A lot of work for a single mark!
Some further examples:
Question 17: Properties of quadrilaterals and angles

Question: Join the dots on the grid (pictured) to make a quadrilateral that has 3 acute angles.
Answer: Any quadrilateral made by joining the dots that has 3 acute angles e.g. an arrowhead shape.
Question 18: Measuring and drawing acute angles

Question: Draw an angle that is exactly 35°.
Answer: An accurately drawn angle.
The mark scheme here allows some room for error – “between 34 and 36 degrees” is acceptable.
Question 19: Measuring and drawing obtuse angles

Question: Draw an angle that is exactly 140°.
Answer: An accurately drawn angle.
As with the question above, a small amount of room for error is given – “between 139 and 141 degrees”.
Question 20: Position and direction (translation)
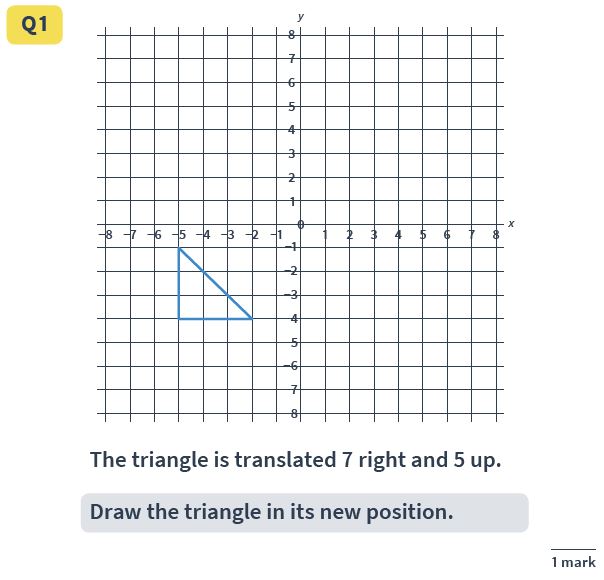
Question: The triangle (pictured) is translated 7 right and 5 up.
Draw the triangle in its new position.
Answer: A new triangle drawn with points at (2,1), (5,1) and (2,4).
Translation can be tricky for pupils. Encourage them to look at the triangle as three points, and to translate each point separately rather than trying to move ‘the whole triangle’.
Explanation questions
An early form of the ‘Prove X’ questions that come up in GCSEs, these problems ask children to explain a mathematical statement or error.
As an example:
Question 21: Reasoning with proportions and distance
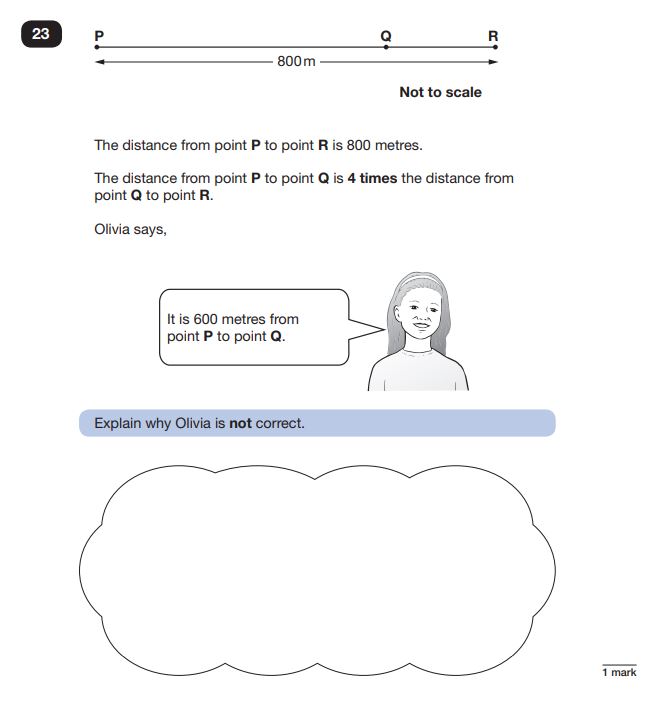
Question: The distance from point P to point R is 800 metres.
The distance from point P to point Q is 4 times the distance from point Q to point R.
Olivia says, “It is 600 metres from point P to point Q”.
Explain why Olivia is not correct.
Answer: If the distance from P to R is 800m and the distance from P to Q is (Q -> R x 4), it must be 4/5 of 800 = 640m. Therefore Olivia is wrong.
More than most problems, this type requires pupils to actively demonstrate their reasoning skills as well as their mathematical ones. Here, pupils must articulate either in words or, where possible, numerically that they understand that Q to R is \frac{1}{5} of the total, that therefore P to Q is \frac{4}{5} of the total distance, and then calculate what this is via division and multiplication.
Further examples from Third Space Learning’s Rapid Reasoning resources:
Question 22: Converting fractions to decimals

Question: Mia says, “\frac{20}{100} is the same as 100 ÷ 20, which equals 5.”
Is Mia correct? Yes / No
Explain your answer.
Answer: No; \frac{20}{100} is the same as 20 divided by 100, which equals 0.2.
Question 23: Order of operations (bodmas/bidmas)

Question: Mia says, “The order of operations means you always carry out division before multiplication”.
Is she correct? Yes / No
Explain how you know.
Answer: No; multiplication and division have the same priority, so in a problem like 40 x 6 ÷2, you would carry out the multiplication first as it occurs first.
The mark scheme notes that vague answers or any answers with a mathematical error are unacceptable.
Question 24: Mathematical proof and counter-examples

Question: Nina says, “When you multiply two numbers together, the answer is always bigger than either of the numbers you started with.”
Is Nina correct? Yes / No
Explain how you know.
Answer: No.
Any explanation that provides a counter-example is acceptable e.g. “Not if the number is 1”, “Not for 0” etc.
Question 25: Place value and rounding logic

Question: Nina says “7,759,532 rounded to the nearest thousand is 7,759,000.” Nina is incorrect.
Explain why Nina is incorrect.
Answer: Any answer that refers to the fact that there is a 5 in the hundreds place, AND a 9 in the thousands place, so that the number has to be rounded up as far as the ten-thousands place.
Sequence questions
Another relatively simple kind of reasoning question, sequence problems involve pupils completing mathematical sequences.
Consider this example:
Question 26: Linear number sequences (multiples)

Question: The numbers in this sequence increase by the same amount each time.
Write the missing numbers.
__, 42, 49, __, 63, 70
Answer: 35, 42, 49, 56, 63, 70
Number sequence questions, particularly those that involve linear sequences or times tables, come up relatively frequently in the SATs maths tests. The question’s instructions point clearly to the solution: work out what the increase between numbers is, then apply this via addition or subtraction to find the missing numbers.
Higher attaining pupils might quickly pick up that this is in fact the 7 times table and rely on their knowledge of multiplication facts to obtain the answer. This should be encouraged, so long as they then check their answer in the normal method to ensure they haven’t made a mistake.
More examples:
Question 27: Fraction sequences
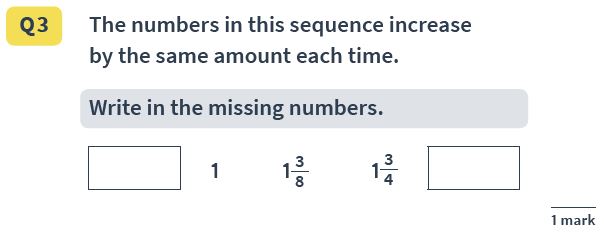
Question: The numbers in this sequence increase by the same amount each time.
Write in the missing numbers.
__, 1, 1\frac{3}{8}, 1\frac{3}{4}, __
Answer(s): \frac{5}{8} and 2\frac{1}{8} (Or \frac{17}{8})
Both answers must be correct to receive the mark. Pupils must recognise that \frac{3}{4} is the same as \frac{6}{8}, so the following number must be three eighths higher.
Question 28: Negative number sequences
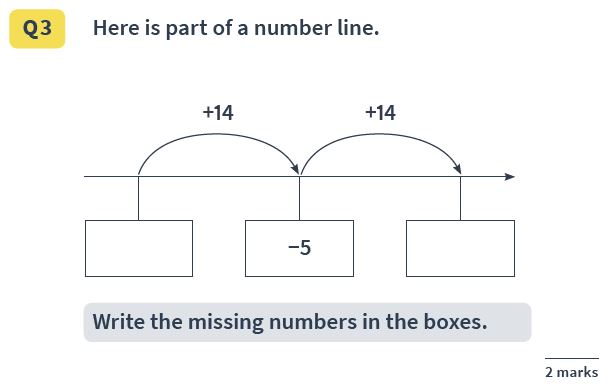
Question: Here is part of a number line (pictured). Write the missing numbers in the boxes.
Answer(s): -19 and 9
Question 29: Identifying patterns in addition

Question: The numbers in this sequence increase by the same amount each time.
Write in the missing numbers in the boxes below.
Answer(s): 128, 135 and 156.
Question 30: Number lines and intervals
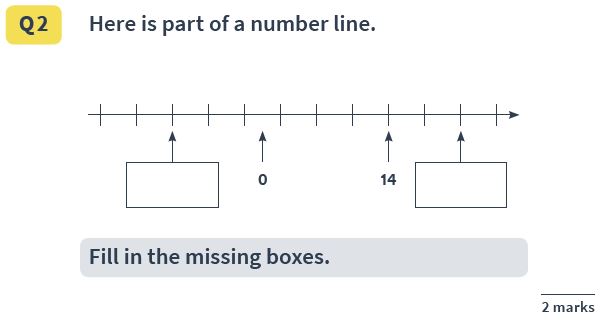
Question: Here is part of a number line (pictured). Fill in the missing boxes.
Answer(s): -10 and 22
This question can be a little tricky; pupils need to work out that the marks on the line represent increments of 4, and count backwards and forwards in 4s to obtain the missing numbers.
Ordering questions
Ordering problems require pupils to put a set of numbers, fractions or measures in the correct order.
A good example is this question from Paper 2 of the 2018 SATs:
Question 31: Ordering fractions (proper and improper)
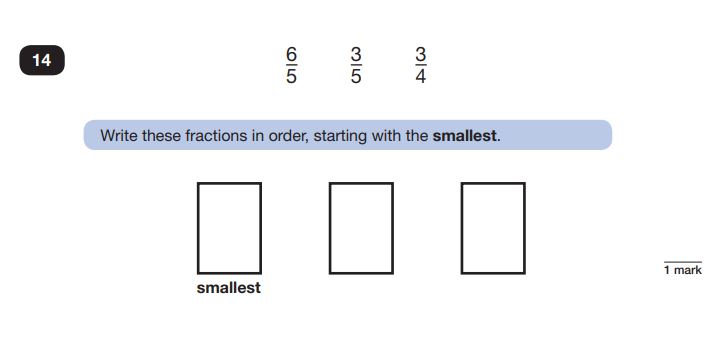
Question: \frac{6}{5}, \frac{3}{5}, \frac{3}{4}
Write these fractions in order, starting with the smallest.
Answer: \frac{3}{5}, \frac{3}{4}, \frac{6}{5}
The improper fraction is a typical complication here. Look out for similar ‘curveballs’ in these questions, including equivalent fractions, mixed numbers, and combined decimals and fractions.
A good knowledge of the fundamentals of fractions is essential here: pupils must understand what a larger denominator means, and the significance of a fraction with a numerator greater than its denominator.
READ MORE: Numerator and denominator
Further examples:
Question 32: Ordering fractions with different denominators

Question: These bottles have different capacities.
A – \frac{4}{5}litre
B – \frac{18}{20}litre
C – \frac{7}{10}litre
D – \frac{3}{5}litre
Write the letters A to D in order from least to most capacity.
Answer: D, C, A, B
Encourage pupils to convert all the fractions to one denominator value to make ordering easier.
Question 33: Comparing and ordering fractions in context
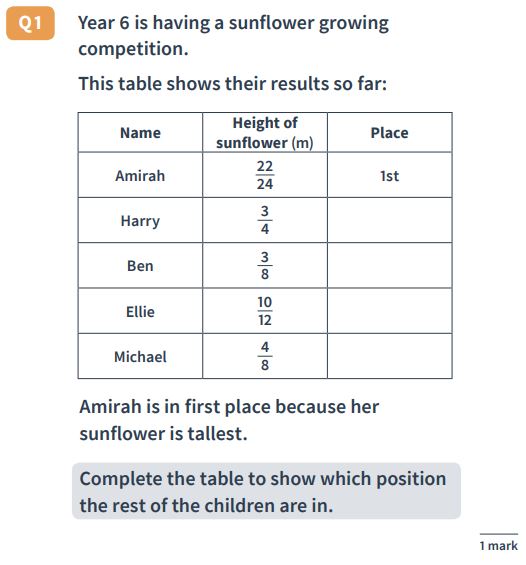
Question: Year 6 is having a sunflower growing competition. This table shows their results so far:
| Name | Height of sunflower (m) | Place |
| Amirah | \frac{22}{4} | 1st |
| Harry | \frac{3}{4} | |
| Ben | \frac{3}{8} | |
| Ellie | \frac{10}{12} | |
| Michael | \frac{4}{8} |
Amirah is in first place because her sunflower is the tallest.
Complete the table to show which position the rest of the children are.
Answer: (descending down the ‘Place’ column) 3rd, 5th, 2nd, 4th
As with the example above, pupils should be encouraged to convert the fractions to make it easier to order them.
Question 34: Ordering decimals
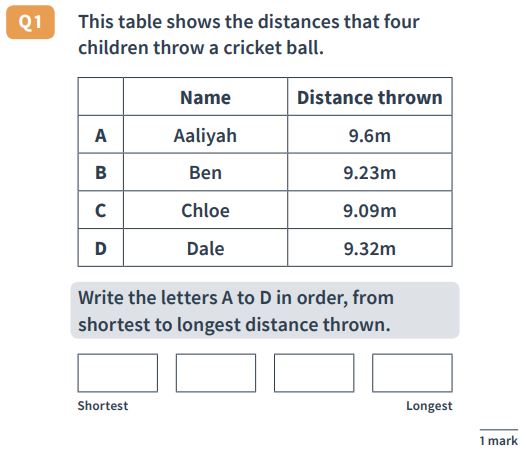
Question: This table shows the distances that four children throw a cricket ball.
| Name | Distance thrown | |
| A | Aaliyah | 9.6m |
| B | Ben | 9.23m |
| C | Chloe | 9.09m |
| D | Dale | 9.32m |
Write the letters A to D in order, from shortest to longest distance thrown.
Answer: C, B, D, A
Question 35: Ordering mixed fractions and decimals
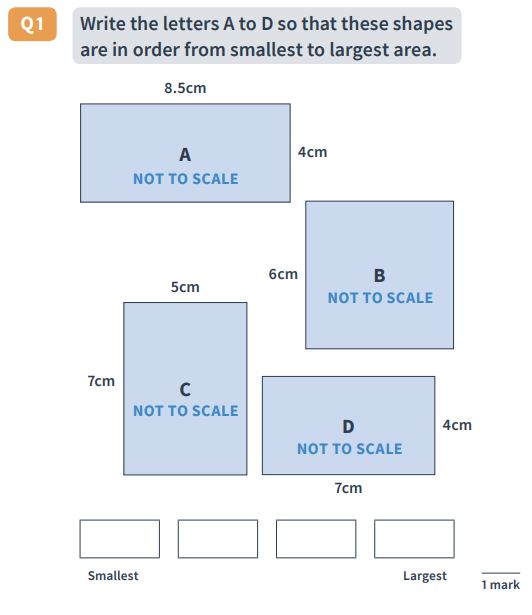
Question: Write the letters A to D so that these shapes are in order from smallest to largest area (pictured).
Answer: D, A, C, B
Why focus on maths SATs reasoning questions?
The KS2 maths SATs are designed to test pupils’ knowledge and understanding of:
- Arithmetic: confidence with core calculations like addition, subtraction, multiplication, and division, including fractions, decimals, and percentages.
- Reasoning: mathematical fluency, logic and problem-solving.
In Year 6, pupils sit a total of 3 maths papers for the key stage 2 SATs:
- Paper 1: Arithmetic (30 minutes)
- Paper 2 & Paper 3: Reasoning (40 minutes each)
There is a greater emphasis on reasoning across the three papers, and reasoning is often considered to be more challenging than arithmetic.
7 top tips for answering SATs questions
Now that we’ve covered how to answer some specific types of reasoning questions, here are some more generic tips for success in the reasoning papers. They may not all be applicable to every single question type, but will apply to at least two, usually more.
- Get pupils in the habit for any practice paper of identifying what information they’re given in a question, and what they need to know to solve the problem. This helps them start to form the steps needed to find the solution.
- Ask pupils to ‘spot the maths’ in a question – which calculations or skills do they actually need to use to solve the problem? This is useful even for arithmetic questions – it’s no surprise how often children can misread a question.
- Check the units! Especially in questions involving multiple measures, it can be easy to give the answer in the wrong one. The answer box might give a specific unit of measurement, so pupils should work to give their answer in that unit.
- Remind pupils to convert different units of measurement in a question into the same unit to make calculations easier, e.g. kg to g.
- Encourage numerical answers where possible. Even in explanation questions, demonstrating the mathematical calculation is a better explanation than trying to write it out.
- The bar model can be a useful way of visualising many different types of questions, and might make it easier to spot the ‘steps’ needed for the solution.
- Check your working out! Even if the working is ultimately irrelevant to the question, you can lose marks if it is wrong.
5 common teacher misconceptions when teaching Year 6 reasoning
Misconception 1: Pupils will automatically transfer knowledge from arithmetic to reasoning.
Fluency in Paper 1 (Arithmetic) doesn’t guarantee success in Papers 2 & 3 (Reasoning). Pupils need targeted practice in interpreting written problems to understand what maths they need to use.
Misconception 2: Reading comprehension is separate from maths.
Pupils often struggle with reasoning questions because of complex language, not lack of mathematical skill. Pupils need explicit practice in deconstructing lengthy word problems and identifying key mathematical vocabulary.
Misconception 3: All multi-step problems require different operations.
Some multi-step problems (like Reasoning Question 7) require the same operation repeated. Teachers should ensure pupils read the context to determine the structure, not just look for multiple keywords.
Misconception 4: If the unit isn’t given in the question, any unit in the answer is acceptable.
While some mark schemes are lenient (e.g., Reasoning Question 13 allows 1.1kg or 1,100g), pupils should still use the context to infer the required unit (e.g., height in cm or m) and they must check the answer box for a specified unit.
Misconception 5: Year 6 pupils no longer need manipulatives or visual models.
To tackle abstract concepts like volume and ratio, visual models act as a bridge, allowing pupils to deepen their understanding. When problem solving, using the bar model or similar visual aids provides a practical way for pupils to structure their reasoning, especially when faced with multi-step problems.
As in-school maths tutoring providers, Third Space Learning works closely with primary schools and teachers across the country who consistently report that their Year 6 pupils find the reasoning papers the hardest. That’s why the Third Space Learning curriculum focuses heavily on developing pupils’ KS2 maths reasoning skills.
We are constantly adapting and building on our programme to ensure it has maximum impact. For example, our primary maths experts found that when reasoning questions were only at the end of a tutoring session, the level of challenge was too high. As a result, they restructured the SATs Booster Programme to introduce maths reasoning earlier. This allows pupils to apply new knowledge immediately and start to embed problem solving skills gradually.
Skye, the AI maths tutor, works through SATs questions at the pupil’s pace and uses spoken prompts to encourage pupils to articulate their reasoning and explain the steps they are taking to solve the problem.
In a survey of schools, Year 6 Third Space Learners did better on their maths SATs than the national average and 9 out of 10 teachers felt the tutoring helped their pupils achieve higher maths SATs scores.
Read our KS2 SATs revision blog for more information on how we’ve structured our SATs revision, and how you can too. Or, watch the top SATs revision topics video.
Comprehensive SATs revision resources
There are hundreds of other free SATs revision resources on the Third Space Learning Maths Hub that you can view online, download and print, including free SATs papers, past SATs papers and SATs intervention packs:
GET THE ANALYSIS ON PREVIOUS SATS
SATs have been running in their current incarnation for 7 years; there were no government standardised assessments in 2020 and 2021 as a result of the Covid-19 pandemic. Get all the analysis and results from previous national assessments below.
And find out which are the top 20 year 6 maths revision topics to focus on this year.
– SATs papers 2025
– SATs results 2025
– SATs papers 2024
– SATs results 2024
– SATs papers 2023
– SATs results 2023
– SATs papers 2022
– SATs results 2022
– SATs papers 2019
– SATs results 2019
– SATs papers 2018
– SATs results 2018
– SATs papers 2017
– SATs results 2017
– SATs results 2016
Maths questions Year 6 and SATs reasoning FAQ
Year 6 maths is designed to ensure students are confident and fluent in the core areas of mathematics before moving to secondary school. Key topics covered include all four operations, fractions, and securing understanding of decimals and percentages. A major focus is on applying this knowledge, especially in problem-solving involving ratio and proportion. Children also deepen their skills in algebra, geometry, and handling data. As the final year of primary education, this year is about consolidating learning across previous year groups.
The most challenging questions for students on the Year 6 SATs often involve multi-step problem-solving. Questions that require converting between fractions, percentages, and decimals can be particularly tricky, as can complex geometry problems. Questions that genuinely push a student’s reasoning skills, especially those involving the interpretation of data or finding a value in a complex ratio problem, are also common high-difficulty items. Good preparation often involves focusing on past paper questions to understand the required form of the answer. At Third Space Learning, we encourage frequent practice week-by-week to build stamina and confidence through engaging lesson starters, games and, where appropriate, one on one tutoring.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out about year 6 sats for your school.


![The Top 20 SATs Revision Topics For 2026 [Video]](https://thirdspacelearning.com/wp-content/uploads/2026/01/SATs-webinar-2025-social-image-6-180x160.png)


