GCSE Maths Paper 3 2023 Summary Of Topics & Questions

Originally published 16th June 2023

GCSE Maths Paper 3 2023 is now behind us and marks the end of this series of GCSE Maths papers. In this blog, we’ll take an in-depth look at Paper 3 Foundation and Higher.

And we’re done! Wednesday (14th June) was the last GCSE Maths paper this year, and students all over the country can begin winding down for a long summer. 

No long summers off for us though, as we’ll be bringing you more analysis of this year’s papers, before returning on Results Day on Thursday 24th August to see how this year’s cohort performed. 

We’ll be taking a look at the Foundation and Higher Paper 3s in detail, but first let’s kick off with a look back at the hit lists for Papers 2 and 3 to see what was missing.

GCSE Maths 2024: Stay up to date

Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2024. We’ll be bringing in our expert contributors to analyse each paper and identify key topic areas to focus your revision.

GCSE 2024 dates
GCSE 2024 results (when published)
GCSE results 2023
Analysis of GCSE Maths Paper 1 (2023)
Analysis of GCSE Maths Paper 2 (2023)
Analysis of GCSE Maths Paper 3 (2023)
Summary of ALL GCSE Maths Papers (2023)

Which topics appeared and which were missing in this year’s calculator papers?

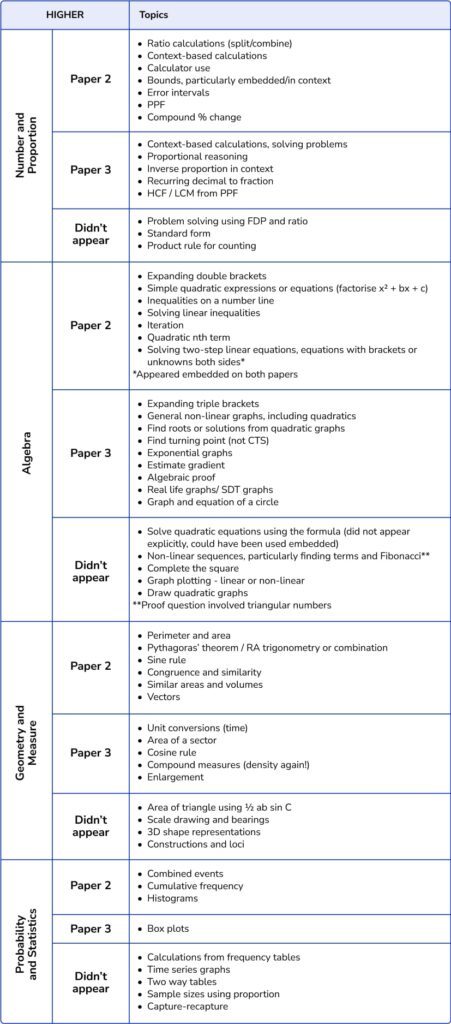
Paper 3 included and repeated some unusual topics

Examiners like to keep us on our toes, so it’s perhaps not surprising after all that there have been a few more unusual topic repeats or gaps. Given that Ofqual are keen to avoid exam papers being too predictable (see “Predicting predictability” (2020) for an interesting look at this), we should expect some degree of error in any revision hitlist.

Focusing on Paper 3, we had:

• A repeat of density at the expense of significant work on speed, particularly on Foundation;
• Cosine rule cropping up on Higher, meaning that nearly all Higher trigonometry content has been assessed in fairly substantial depth this series;
• Product of primes appearing again – on Paper 3, students were asked to use PPF to find the HCF and LCM;
• Simple interest, which definitely gets forgotten about as a potential topic, because it has only appeared once before in the history of the specification.

Paper 3 also left some gaps at both Foundation and Higher

We shouldn’t expect every topic on a revision hitlist to appear within a series, because these lists are often quite extensive and cover possibilities rather than predictions.

There were, however, a few big gaps left by Paper 3, particularly:

• Limited work on graph plotting, particularly linear or quadratic graphs, on either tier;
• Anything involving double brackets on Foundation;
• Pythagoras and trigonometry on Foundation (excepting exact trig values on Paper 1);
• Statistical calculations on Higher – all work on averages and spread involved estimating or reading these from a graph.

Look out for the next blog in this series which will be a summary analysis of all three 2023 papers with more in-depth discussion of content gaps in the series as a whole.

Student responses to Paper 3

Student consensus on social media seemed to be that Paper 3 was fine, with a few candidates really happy with their performance and a “beautiful, lifesaving” paper:

Jonny’s question about coffee (second question in the crossover content) obviously got a lot of meme attention:

Lots of Higher candidates found the surface area of a frustum question tricky!

And candidates were quick to point out that a lot of their exam aids and equipment was useless!

This cohort is now done with GCSE Maths, and some are very happy to never think about maths again. But let’s take a look in more detail at the final papers, and see if student reactions to an “easier” paper were justified.

What was the process behind this Maths Paper 3 analysis?

In this blog, I’ve used the same processes and classifications as in my previous exam analysis blog posts:

• Question Level Analysis Of Edexcel Maths Past Papers (Foundation) (2017-2019)
• Question Level Analysis Of Edexcel GCSE Maths Higher Past Papers (2017-2019)

And 2022’s series of exam paper analysis blogs:

• GCSE Maths Paper 1 2022
• GCSE Maths Paper 2 2022
• GCSE Maths Paper 3 2022

You can read in more detail about the processes used in my GCSE Maths Paper 1 2023 blog.

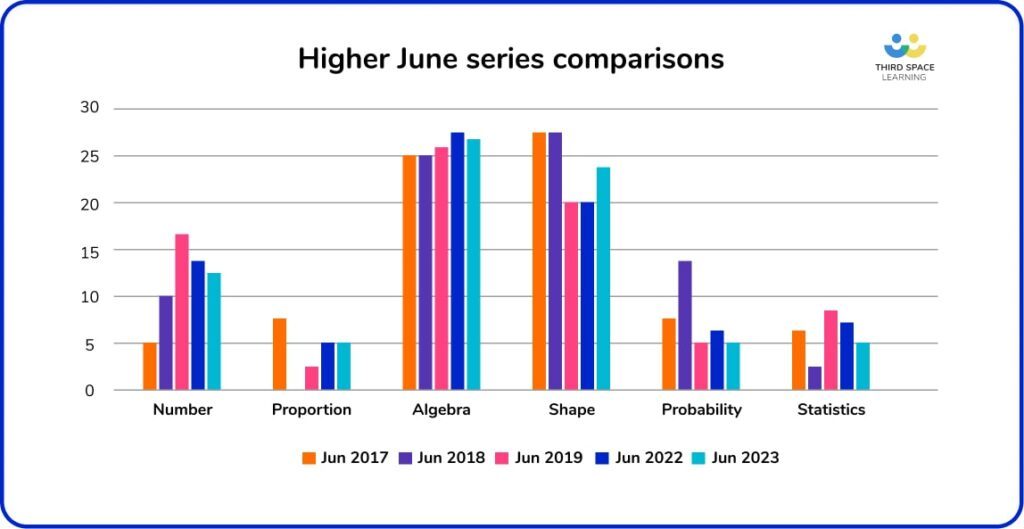
The suggestions in this blog are based on data analysis of four series of June papers that were actually sat by students, i.e. June 2017-2019 and 2022 exam papers.

These are only ever going to be informed recommendations from me so we leave it, of course, to your professional judgement to decide on what to do with the information.

Detailed analysis of Paper 3 Foundation

Paper 3 Foundation was fair and accessible, continuing the theme of this year’s maths papers

In my previous articles, I described Foundation Papers 1 and 2 as fair and accessible to a cohort who had experienced disruption to learning as a result of the Covid-19 pandemic.

Continuing this theme, Paper 3 was so ‘fair and accessible’ (dare I say, easy?!) that it felt like it could have fitted well into the pre-2015 GCSE specification. Like the rest of the series, the paper ramped very slowly, with lots of one-mark procedural questions in the first half. 

In fact, candidates had to get all the way to Q9 before tackling a question part worth more than one mark, and this was a very straightforward median from a list of four numbers, and then drawing a simple bar chart.

There were a couple of trickier bits in the crossover content. For example, the 5-marker question required applications of angle reasoning, including angles in a triangle, on a line and in parallel lines. Additionally, the more unusual combination of standard form and ratio in the final question may have thrown some students. However, there was also some straightforward stuff up for grabs here, including another procedural density question.

Standard procedural questions made up a larger majority of this year’s Paper 3

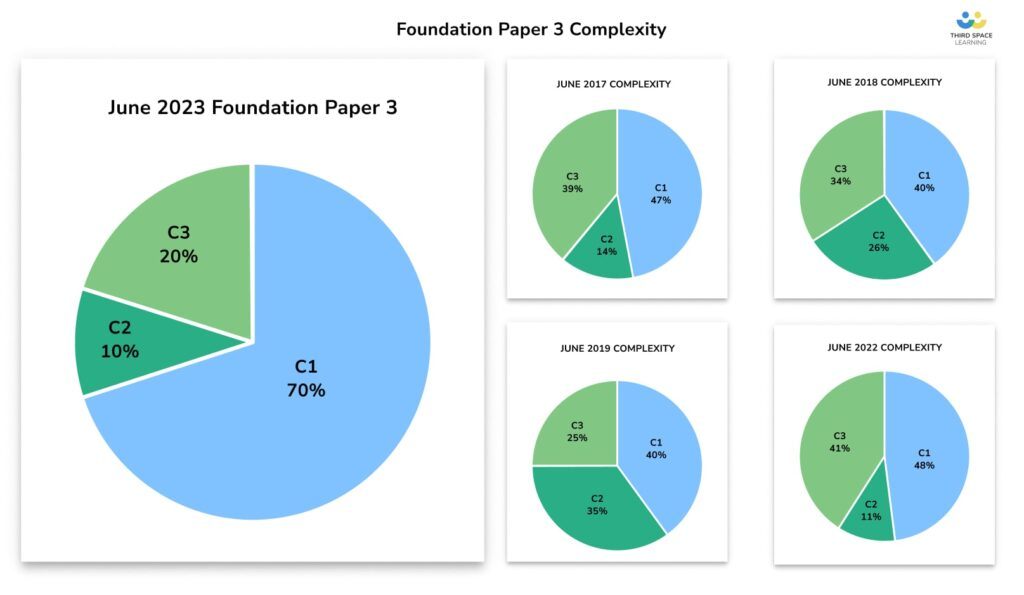
When looking at complexity, we can perhaps see why the paper feels easier than previous past papers. I categorised 70% of the paper as C1 (standard procedural questions). 

The proportion of C2 marks (interpret/explain/show that) is comparable to last year’s Paper 3, but there were fewer multi-step unfamiliar problems on this paper than usual. I suggested in my Paper 2 blog that we might see more C2 on this paper with more work on charts and graphs – for example, identifying errors on a graph – but this did not materialise.

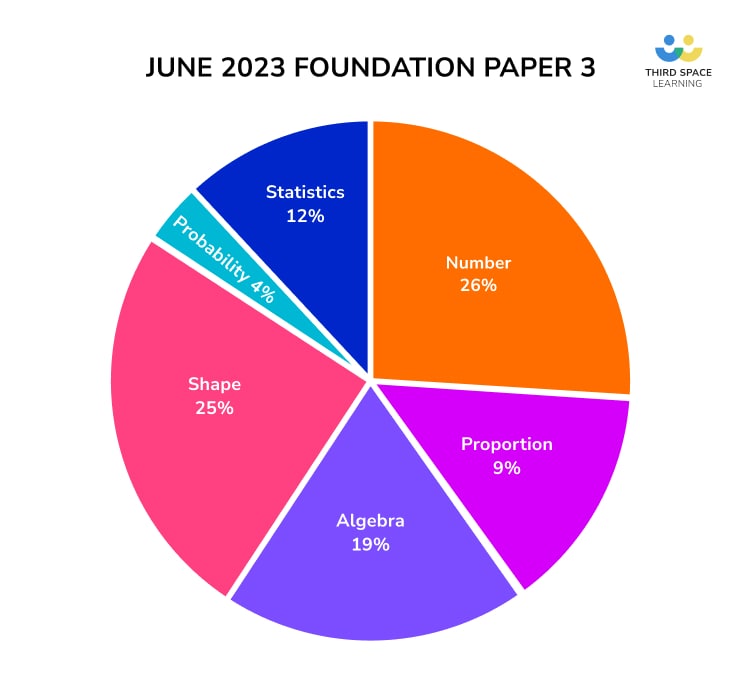
Paper 3 was light on Shape content and left gaps in Algebra

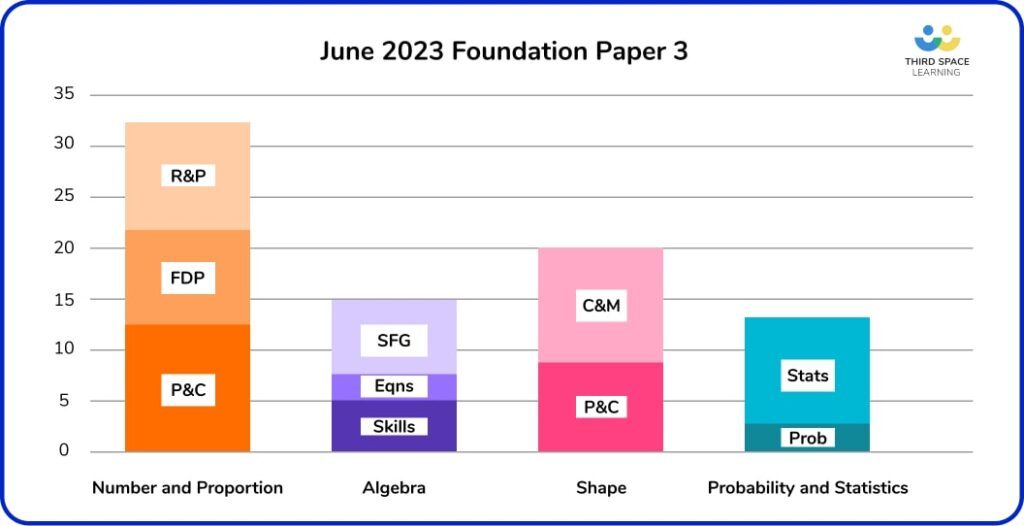
As expected, we had a bit more Algebra and Proportion on this paper compared to Paper 2, with some gaps being filled in. That said, it felt like there were some quite large gaps left in Algebra, particularly in graph work.

We saw a bit more Shape Properties and Constructions on this paper, and, as suggested, angle facts did appear again on this paper (the aforementioned 5-marker). However, the overall Shape content still felt quite light, and it was surprising that there was nothing on Pythagoras and Trigonometry, other than a one-mark question on exact trig on Paper 1.

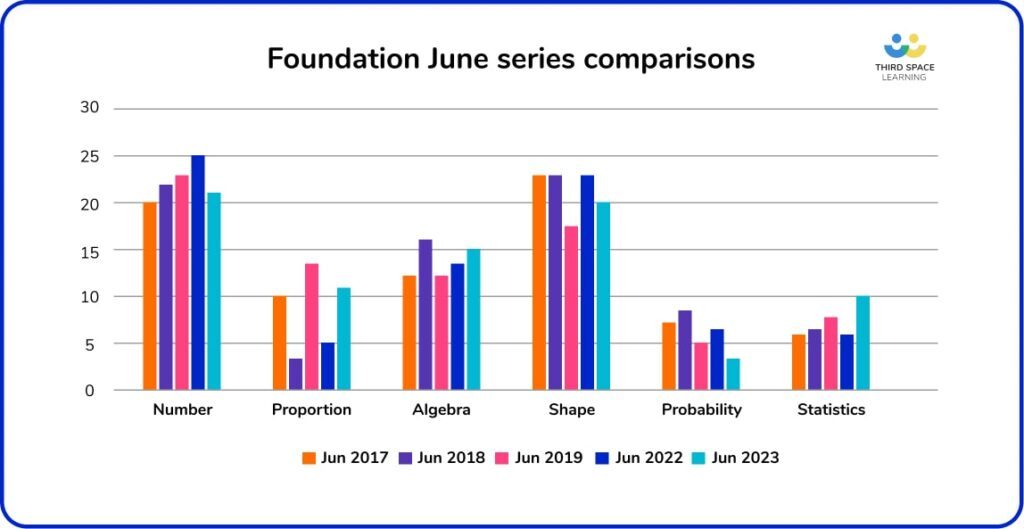
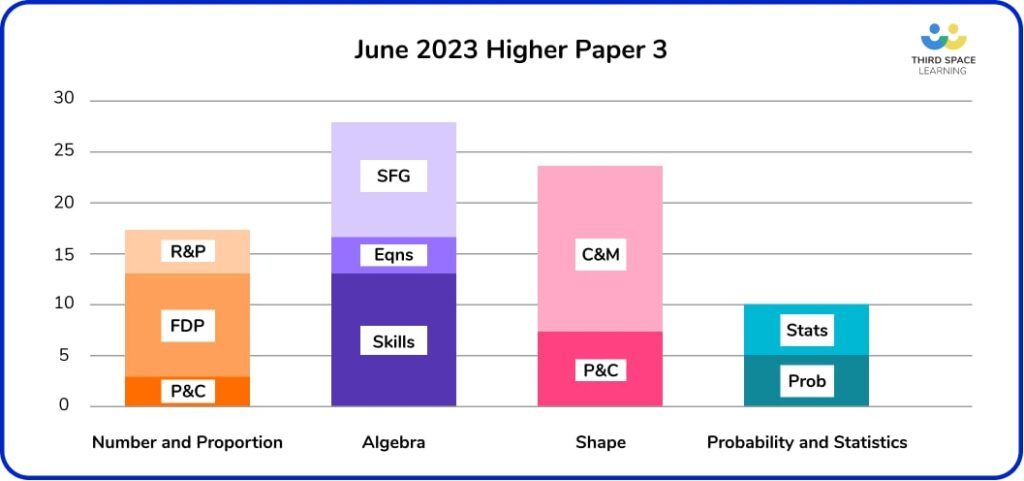
Detailed analysis of Paper 3 Higher

Paper 3 Higher started with accessible questions with more challenging content cropping up later

The Higher paper also started nicely, with procedural work on laws of indices followed by a fairly simple problem about coffee to solve using percentages. Also in the crossover section, the density and quadratic graphs questions in particular felt like places to pick up a few easy marks.

There were a couple of trickier problems requiring a bit of creative thought, including Q12 (the proof using triangular numbers) and Q15b (application of DOTS). These weren’t worth many marks, but it may have thrown students with these appearing relatively early in the paper.

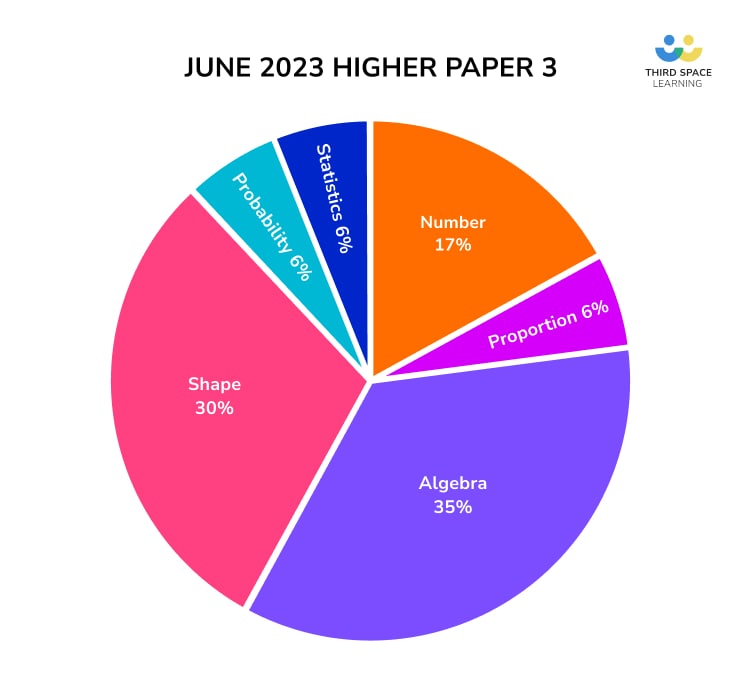
Paper 3 included fewer C3 questions with a skew towards C2

The proportion of standard procedural (C1) questions on this paper was comparable to previous series, but there was more of a skew towards C2 over C3 questions, with lots of “show that” questions, and 11 marks on reasoning or formal proof.

Following a trend over the three papers, this Paper 3 has the lowest proportion of C3 questions of all of the summer series so far.

Paper 3 filled some gaps in Algebra and Shape and included a somewhat surprise appearance 

As expected, there was plenty more work on Algebra and Shape, filling in some of the gaps from Paper 2. In fact, the second half of the paper felt very algebra-heavy, particularly the vector problem using algebra (Q22, 3 marks) and the algebraic fraction from a combined events scenario (Q24, 5 marks).

Despite having a fairly high proportion of Shape work, this was again more concentrated in Calculations and Measures than Properties and Calculations, leaving a few gaps here.

Statistics and Probability were fairly evenly balanced on this paper. It was unusual, although not entirely unexpected, to see box plots on this paper given that we’d had most other Higher charts and graphs on the previous papers – perhaps an example of the examiners keeping us crystal-ball gazers on our toes!

What’s next for GCSE Maths 2023?

With the exam papers out of the way, we’ve got a couple more things coming up for you on this year’s GCSE Maths papers.

In late June, we’ll be back with an in-depth analysis of all three June 2023 papers. This time, we’ll have a more forward-looking view to see how you might use this series of papers to shape teaching and revision priorities for next year’s exam cohort.

And finally, we’ll be back for GCSE Results on Thursday 24th August to have a look at how this year’s cohort got on with the papers we’ve discussed in this series.

You can also read our analysis of Paper 1 & Paper 2 this year:

• GCSE Maths Paper 1 2023
• GCSE Maths Paper 2 2023