How To Revise For Maths: 8 Tried And Tested Strategies To Help Your Students
Teaching students how to revise for maths is often overlooked and new topics are prioritised. It is essential to review and reinforce learning to strengthen students’ grasp of mathematical concepts and fill knowledge gaps through maths revision.
This article explores everything you need to know about preparing students for maths exam papers. You’ll find a variety of practical and straightforward revision tips maths teachers can use to teach students how to revise for maths effectively.
Teaching students how to revise for maths
Knowing how to revise for maths, particularly GCSE maths and GCSE maths resits, involves specific revision techniques and strategies that enhance the retention of maths knowledge.
While effective revision is generally personalised and self-led, most students need plenty of support from their teachers to develop the independent study skills required to get the most out of their revision time.
Ultimate guide to GCSE maths revision
Strategies and practical techniques for maths teachers and subject leaders to support and teach students how to revise for maths effectively.
Download Free Now!When should you teach students how to revise for maths?
While it may be tempting, do not leave teaching students how to revise for maths until a few weeks before a maths exam, or worse, last minute. Prepare students with revision techniques to help them succeed at every step and level of maths they work at.
Encourage good study habits from Key Stage 3 to build a strong foundation for the examination years.
It’s helpful to teach revision skills explicitly alongside the maths syllabus, regardless of whether they are general skills or more maths-specific.
READ MORE: KS3 Maths Worksheets For Effective Learning

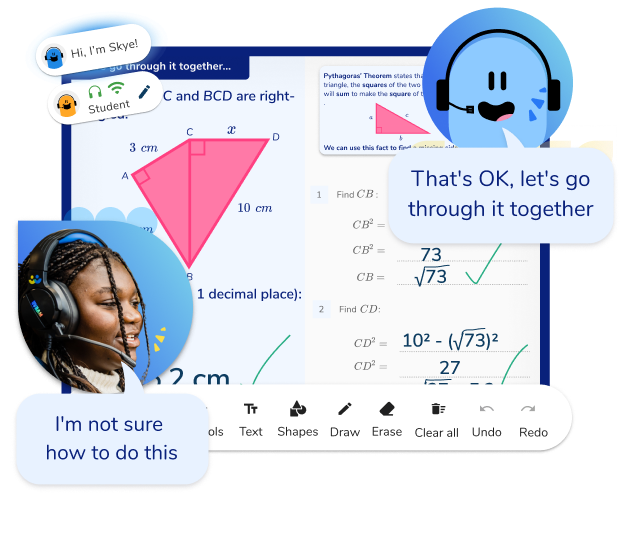
Unlimited GCSE maths tutoring with Skye, the voice-based AI maths tutor.
Built on the same principles, pedagogy and curriculum as our traditional tutoring but with more flexibility, reach and lower cost.
Help your GCSE students achieve their target grade with Skye’s one to one maths tutoring.
Watch Skye in actionHow to revise for maths: 8 strategies that work
The strategies outlined here are applicable across the full secondary age range. Early implementation increases their effectiveness when students reach Key Stage 4.
Integrating these strategies into tutorials and classroom practice helps students develop skills and habits for independent learning and revision.
1. Practice testing
In 2013, John Dunlosky identified practice testing as one of the most effective learning strategies. Practice testing is simply testing knowledge or understanding in a low-stakes environment.
Common strategies for practice testing include:
- Summaries of key information
- Flashcards
- Past exam questions
Dunlosky mentions three key components for successful practice testing:
- Make notes to support later practice testing
- Recall from memory as opposed to choosing from multiple-choice answers
- Continue practice testing until each concept has been correctly recalled from memory at least once
Continue practice testing until students correctly recall each concept at least once from memory. Although a growth mindset is important, emphasise the importance of ‘getting things right’ when revising.
While this does not need to be immediate, encourage resilience in your students and not to give up or brush off difficult concepts.
Flashcards for practice testing
Flashcards are an effective technique for memorising key mathematical formulas. Students should:
- Make them with a prompt on one side and the answer on the other
- Work through them and put the correctly answered cards in one pile, and the incorrectly answered cards in another
- Repeat the process until all cards are recalled from memory at least once — the crucial part is to review the unknown ones again

Third Space Learning’s GCSE revision cards.
Here, personalisation is important. The concepts students need help to ‘get right’ will vary from learner to learner. Students may need to work independently to review material relevant to their gaps in knowledge and understanding.

Third Space Learning’s one to one approach allows tutors to adapt lessons to suit each student’s ability, helping them understand and revise difficult maths concepts.
Students work with the same tutor each week to build rapport. Tutors quickly understand students’ preferred learning styles and use the appropriate teaching strategies to teach and revise maths concepts students struggle with.
Worked examples for practice testing
Worked examples are crucial for understanding maths problems. Ensure students have a dedicated place for these examples, whether in their exercise book, a separate book, or on flashcards, to avoid confusion during revision.

Third Space Learning tutors encourage students to explain their thought process verbally and in writing. This ensures maximum maths fluency rather than rote memorisation of methods.
Best practices for worked examples
Often, students don’t see the value of illustrative worked examples or struggle to use them for revision for a variety of reasons, including:
- They cannot locate the required examples in an exercise book
- Errors when copying examples
- Too many worked examples to choose from
- Examples include multi-topic content
To avoid this and avoid organisation issues when students are revising, provide students with a dedicated place for important worked examples:
- In a different section of their standard exercise book
- A stand-alone smaller book
- On flashcards or in a folder
Think carefully about the worked examples chosen, particularly in selecting a variety of digits or numbers and ensuring that the arithmetic involved doesn’t significantly increase the cognitive load of the problem.
Ofsted’s 2023 report, Coordinating Mathematical Success, notes that unplanned examples with poor method selection can hinder revision. Carefully choose examples to ensure clarity and effectiveness.
Digital examples
Digital examples, such as video tutorials, can help some students understand how to revise for maths. Students often prefer to “talk through” a worked example in addition to seeing it written on a page. This helps students visualise the steps.
Provide students with a QR code to access these resources for independent revision, such as those in the Third Space Learning video series. These are useful for problem solving, particularly multi-step problems.
2. Encourage memory recall
German psychologist Hermann Ebbinghaus developed a ‘forgetting curve’ which shows students forget most newly learned concepts if not reviewed regularly.
Regular review helps retain new concepts. Use frequent retrieval practice to flatten the forgetting curve and enhance long-term memory.
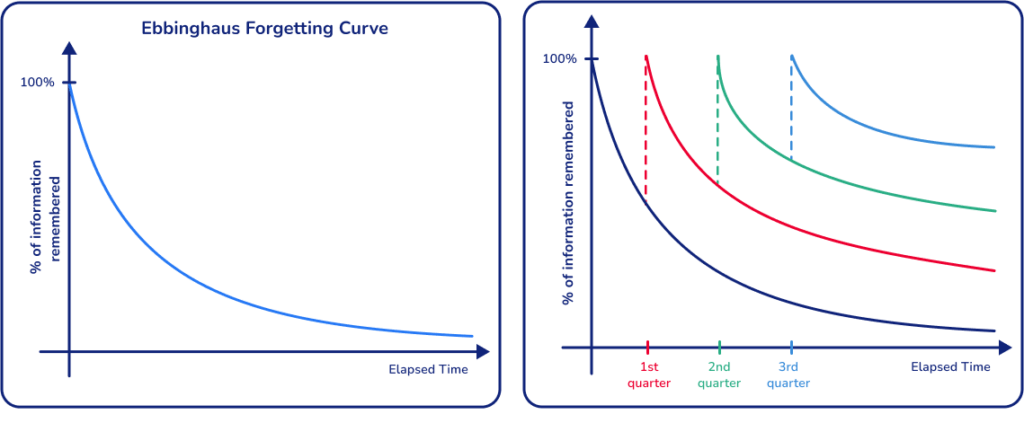
Third Space Learning sessions offer students the opportunity for regular practice to ensure maximum retention of key maths concepts ahead of their exams. The one to one approach means that tutors can focus on the revision topics that each student is specifically struggling with — at a pace that suits them.
Dunlosky suggests that almost any kind of practice testing benefits student learning. But, students benefit most from tests that require memory recall rather than tests which require the selection of a correct answer.
While memory and cognitive theory are at the forefront of educational discussion, the ideas involved are fairly intuitive and come naturally to many experienced practitioners.
Often, these ideas are not communicated to students. Students should also understand particular pedagogical decisions for revision techniques and revision strategies.
For example, if your school uses Fluent in Five at the start of every maths lesson, explain why these lesson segments are important and how students can maximise their learning during these parts of the lesson.

3. Distributed practice
Short, frequent study sessions are more effective than long ones. Encourage students to study in 20-minute chunks rather than cramming.
This principle does not only apply to revision for maths tests. Students can use this strategy when completing weekly homework or general review of class work.
Deliberately engineer tasks so that students can’t complete the entire sheet immediately e.g. set tasks that require content from later in the week.
4. Revision timetables
Students often struggle with the idea of distributed or spaced practice for revision and instead, opt to cram large chunks of information before an exam or assessment.
Encourage and help students to devise a revision plan that distributes topics or subjects evenly. Or provide a revision guide for them that utilises interleaving rather than blocked practice. This will not only help students understand how to revise for maths but also how to revise for GCSEs and reduce exam anxiety.

Download the Third Space Learning revision timetable template to fill in with students.
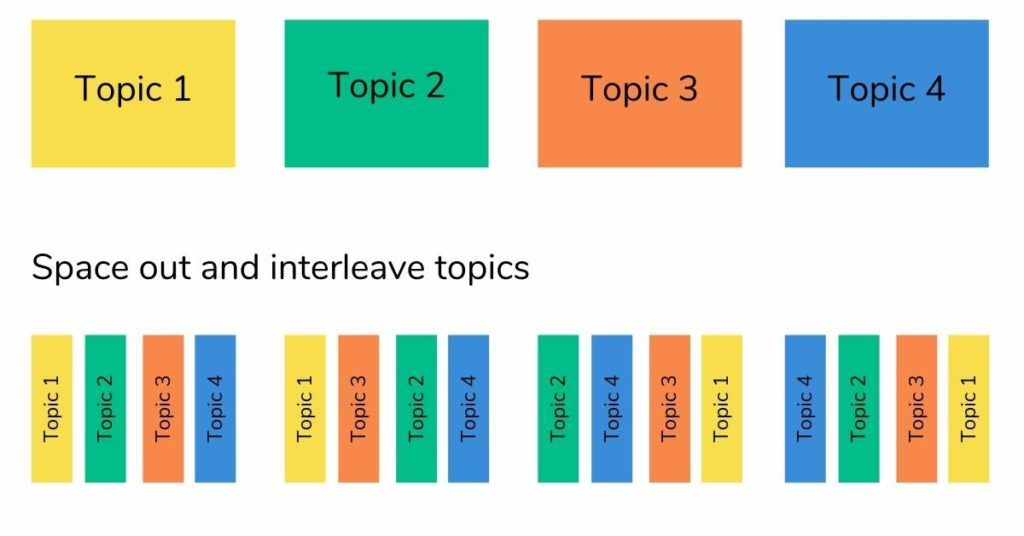
5. Interleaved practice
Interleaving maths revision involves alternating between topics during revision. While it may slow initial learning, it significantly improves retention and understanding.
Student resistance to interleaving is likely as it slows initial learning. Communicate to students the ideas and principles behind interleaving and explain how this revision technique will improve their maths revision.
How to space interleaved practice
- Revisit newly learned concepts frequently – include a recap in the next couple of lessons, within a week and then within a fortnight
- Revise older concepts less frequently but ensure they’re mixed in with other newer concepts
- Explicitly link to prior knowledge and concepts wherever possible and include practice on these concepts (e.g. include fractional coefficients when solving equations)
6. Practice past papers
Practice papers are integral to GCSE maths revision, particularly in preparation for GCSE maths exams. They help students practice questions under timed conditions and develop a good exam technique.
As a department decide which papers to use for maths revision. No one should use the paper chosen for the November mock exam in a revision session.
There are a variety of ways to organise and use past papers during revision sessions for students:
1. Timed practice
Students complete the past paper under exam conditions. Allow students the same amount of time as they receive in the exam, cover all information on the walls and only allow students the materials they will have in the exam. This helps students to identify any learning gaps and areas of maths they need to work on in timed conditions.
2. Grouping
Group similar questions together into individual topics to create topic packs based on students’ learning gaps. If you know students need to improve on trigonometry, create a bank of maths questions on this topic to work through.
3. Perfect past papers
Make a perfect exam paper. You can use the mark scheme and past paper questions to create a set of model answers for students to refer to. Put these on flashcards for students to use during revision.
4. Practice every day
Some schools send past papers home with students who then complete sections of the paper in an independent revision session. Encourage students to complete just one or two practice questions each day.
Over time, they will complete several exam papers and secure their understanding of different topics and maths knowledge.
Prompt students to make revision notes on any concepts they struggle with to strengthen their long-term memory.
At Third Space Learning, our past paper sets contain three papers and replicate real-life GCSE Maths past papers. Written by experienced teachers and examiners, the questions match the three main exam boards, Edexcel, AQA and OCR.
Explore the full range of maths revision resources including revision mats, revision PowerPoints and topic worksheets in the Secondary Maths Resource Library.
7. Elaborative interrogation and self-explanation
These linked strategies encourage students to read actively, increasing the information retained.
- Elaborative interrogation involves students explaining why a fact is true. For example, an explanation for why the interior angle sum of a hexagon is 720° might rely on a student splitting the shape into four triangles.
- Self-explanation involves students linking new knowledge or information to something they already know. For the hexagon example, the student might link this knowledge about the interior angle sum in a hexagon to other simpler shapes.
Dunlosky highlights these techniques have no benefit when solving practice question sets. However, they can show significant promise when students face non-standard or unfamiliar problems.
Self-explanation is likely the more effective technique for mathematics revision. Michael Pershan shared his thoughts about worked examples. He believes students can develop their self-explanation abilities. To do so, they should use self-explanation prompts alongside worked examples.
How to use self-explanation prompts:
- Get students to think about generalisations that they may otherwise miss.
- Direct attention to the most important parts of a worked example.
- Do not need to be independently created – some students may benefit from a framework or a gap-fill approach.
Self-explanation prompts:
- ‘What is the first step in this problem?’
- ‘Could we write here? Why/why not?’
- ‘What would happen if we did first?’
- ‘What are the clues in the question that lead us towards as the first step?’
- ‘Explain how we know is an unreasonable answer to this problem’
- ‘How does this step tie in with what we learned previously about ?’
- ‘What’s similar/different about this problem compared to previous work?’
Third Space Learning tutors are trained in effective questioning techniques. They encourage students to participate in their learning and use mathematical dialogue.
8. Tutoring
Some students need more than study tips to help them learn how to revise for maths. Personalised maths tutoring, like Third Space Learning’s one-to-one sessions, can significantly improve maths understanding and confidence.
Schools may choose to use staff to provide small group tutoring or use external providers for one to one revision sessions.
Whether individual or in a small group, tuition is most effective when it is done in partnership with the school. Ofsted recently highlighted that tutoring provision is strongest when “other adults working with students, including […] tutors, understand the curriculum and its implementation.”
Third Space Learning’s personalised GCSE Revision Programme is designed specifically for Year 10 and 11 students in secondary schools and academies who are struggling with maths or lacking in confidence.
One-to-one tutoring is a highly flexible way to raise maths attainment, up to 20 students can receive tuition at once without disrupting the regular timetable.
Tutoring programmes easily fit into school schedules, curriculum and maths lessons, minimising disruption while maximising impact.
If you want to remind students of these strategies for how to revise for maths, you can also download a high-quality PDF version of the GCSE revision tips poster below for free!

Learning how to revise for maths and mastering maths revision is more than covering the syllabus, it is crucial for early success.
Embedding revision techniques such as practice testing, worked examples and interleaving practice can enhance students’ mathematical understanding and retention.
Early and continuous integration of evidence-based revision techniques enhances mathematical understanding and retention, preparing students for exams and lifelong learning.
How to revise FAQs
To achieve a 9 in GCSE maths, start revision early. You don’t need to cover all of the course content before you revise. Use spaced practise to cover previously learned topics, focus on your weakest concepts. Add new topics as they are covered.
People find different techniques work better than others. Some suggested revision techniques and strategies include:
• Write a revision plan or timetable
• Organise revision notes
• Read revision notes or write out repeatedly
• Past exam papers
• Practice doing the exam.
• Get support, such as tutoring, if required
Firstly, create a revision timetable and stick to it. You can include various methods of revision. Some methods to revise maths well include:
• Flashcards
• Retrieval practice
• Past papers
• Worked examples
Use a range of revision strategies that work for you to embed maths knowledge in preparation for end of year exams or formal examinations such as GCSEs and A-levels.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Skye – our AI maths tutor built by teachers – gives students personalised one-to-one lessons that address learning gaps and build confidence.
Since 2013 we’ve taught over 2 million hours of maths lessons to more than 170,000 students to help them become fluent, able mathematicians.
Explore our AI maths tutoring or find out how our GCSE maths tutoring programmes could support students in your school.