Supercharge Your Higher GCSE Maths Lessons: An In-Depth Question & Topic Analysis Of Edexcel Higher Maths Papers 2017-2023
GCSE maths Higher past papers can be very useful in preparing students for the upcoming exams. For school leaders or maths teachers, we’ve made an extensive guide outlining topics and questions from previous GCSE Edexcel higher maths exams.
It is important to note that this blog focuses on Pearson Edexcel maths past papers, not the AQA or OCR exam boards, nor IGCSE maths. The focus will be solely on GCSE maths, not A Level maths or the maths Edexcel A Level.
GCSE MATHS 2024: STAY UP TO DATE
Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2024. We’re analysing each paper during the course of the 2024 GCSEs in order to identify the key topic areas to focus on for your revision.
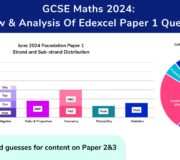
Thursday 16th May 2024: GCSE Maths Paper 1 2024 Analysis & Revision Topic List
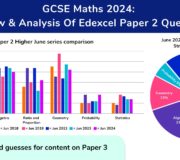
Monday 3rd June 2024: GCSE Maths Paper 2 2024 Analysis & Revision Topic List
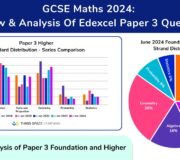
Monday 10th June 2024: GCSE Maths Paper 3 2024 Analysis
GCSE 2024 dates
GCSE 2024 results (when published)
GCSE results 2023
Edexcel maths past paper findings
If you are short on time, here are my key takeaways from the past paper analysis. You can read in more detail about each strand later in the article, along with tips for which topics to focus on in the first few questions, common questions, and so on.
Number and proportion
- Basic calculation skills (four operations and working flexibly with fractions, decimals, percentages, and ratio) need to be automatic.
- There is some accessible procedural work on standard form, HCF and LCM, negative and fractional indices, surd manipulation, expressing recurring decimals as fractions, using a calculator and error intervals, on most maths Higher past papers.
Algebra
- Basic algebra skills (simplify, expand, factorise, solving equations and inequalities) need to be automatic. Algebraic fractions are frequently used to assess a range of algebraic manipulation skills.
- Linear and quadratic equations and inequalities are frequently assessed in a variety of contexts, particularly perimeter, area, and volume.
- There is some accessible procedural work within sequences, functions, such as quadratic nth term, inverse and composite functions, basic graph skills, equation of a straight line, drawing graphs, and estimating solutions from a graph.
- Other key topics include: simultaneous equations, including non-linear, expanding triple brackets, solutions of equations using iteration, gradients and areas, particularly using speed-time and distance-time graphs.
Ratio and proportion
- Proportional reasoning, particularly ratio, is assessed throughout the paper, and lack of understanding could limit accessibility of other topics.
- This strand is particularly context-heavy: ensure students are familiar with common real-life contexts by explicit teaching of problem-solving.
- There is increased emphasis on compound measures, particularly speed and density; these topics are often interwoven with others, such as volume and surface area.
Geometry
- Perimeter, area, and volume is almost exclusively assessed in context and links heavily to other topics, such as linear and quadratic equations and inequalities.
- Pythagoras and trigonometry has a stronger focus on problem-solving/multi-step problems requiring applications of more than one rule, working in 3D or applying to area calculations.
- Candidates need to be able to give clear mathematical reasoning for 2D shape and angle problems; angles in polygons and circle theorems feature here.
Probability
- There is plenty of accessible procedural work on combinations, Venn diagrams and tree diagrams.
- Extend higher-attaining students with plenty of practice with combined event problems.
Statistics
- Presenting data mostly involves drawing and interpreting cumulative frequency graphs, box plots, histograms, frequency polygons; candidates are just as likely to be asked to interpret or critique a given chart or graph as to draw one themselves.
- Processing data focuses on estimating the mean, and calculating averages and ranges from charts and graphs (such as finding the IQR from a box plot).
Practice Paper Pack: Edexcel Higher 2023 Set 2
Download this free pack of Edexcel Higher practice papers for 2023, this resource will get you ready for the exam.
Download Free Now!Background to this research
I first started looking in detail at these papers in 2021, when I used the then available full set of six Edexcel GCSE maths Higher papers from June 2017 through to November 2019.
Since writing that article, we’ve had a few more sets of papers and I’ve had more time to refine my analysis process. This refreshed article takes a look at all Edexcel Higher series so far, and answers these questions:
- Higher analysis by strand and topic – which strands or topics are the heaviest hitters at Higher level?
- Which topics appear the most in common or crossover questions at GCSE?
- Which topics appear in the first half of the paper at Higher level?
- Which topics are more likely on Maths Paper 1?
Edexcel past papers methodology
Categorising by topic
When I began my analysis work on the first six sets of Edexcel past papers a couple of years ago, I applied a broad approach to categorise each question, using only topic and sub-topic (for example, Statistics / Charts and Graphs). Since then, I have added several more papers and further detail to my data-set, allowing for a more in-depth look at how different topics are examined.
The categorisations are based on the GCSE specification (Edexcel), and align closely with Third Space Learning’s topic categories.
As for my Foundation analysis, classifying some of the multi-mark, deeper problem-solving questions presented a bit of a challenge. I decided to pick a main topic for each question and classify under that heading, rather than try and assign marks for topics within questions.
So, for example, June 2017 P1 Q18 required candidates to apply knowledge of properties of a rhombus to a question about linear graphs. However, as the question is inaccessible without knowledge about the general equation of a straight line, I classified this as ‘linear graphs’.
It should be noted that the proportional reasoning category only covers standard proportion and ratio-type problems – so recipes, conversions, splitting into ratios and so on. However, many ratio problems do include fractions, percentages or both.
Third Space Learning’s online GCSE mathematics courses cover the entire GCSE mathematics curriculum. They use diagnostic testing to assess where the gaps in knowledge lie and then use this information to tailor the course specifically to the needs of each student. These individualised lessons help students to practice the areas of maths they need more support on. This helps them to develop mathematical fluency and increase their confidence going into the GCSE maths exam.
Categorising by complexity
In order to simplify the analysis process, I decided to classify the high-mark problem-solving questions by their main topic; this does lose a little bit of detail but makes it easier to look for trends across a larger data set.
I also wanted an idea of the difficulty or complexity of each question. I decided to base this broadly on the GCSE assessment objectives:
AO1 – using and applying standard techniques (50%)
AO2 – reasoning, interpreting and communicating mathematically (25%)
AO3 – solving problems in mathematics and other contexts (25%)
It should be noted that this is a very rough basis, as longer or multi-step questions often award marks for more than one assessment objective. My complexity classifications can be stated as follows:
C1 – standard procedural problems, often worth one or two marks
C2 – problems asking candidates to explain their reasoning, interpret information from tables, diagrams or other contexts, or ‘show that’ type questions
C3 – non-standard multi-step problems, often requiring the application of skills from a variety of topics, worth three, four, or more marks
This is also not a ‘difficulty’ measure. It should be noted that ‘higher grade’ topics, such as simultaneous equations or estimating the mean, are often examined as standard procedural.
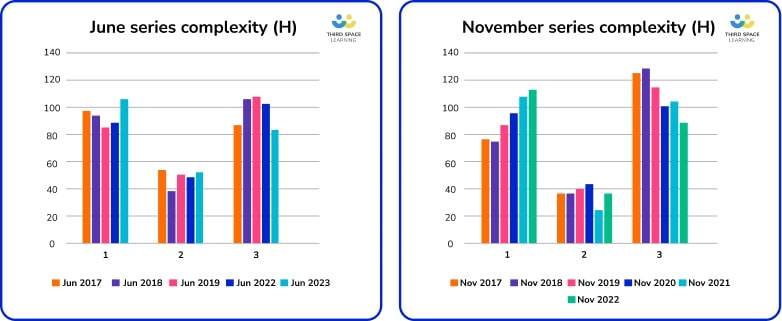
Generally, between 40-50% of the marks were allocated to C3 problems; obviously within this there will be some A01 marks for applying standard techniques. However, this emphasises the expectation that Higher maths candidates should be able to reason flexibly with their mathematical knowledge, rather than just apply to standard problems.
Prior to 2020, the November series seems to favour a slightly higher ratio of C2/3 to C1 questions. Post-2020 papers trend towards a slightly higher ratio of C1 to C3 questions; this difference is particularly noticeable on the June 2023 exam papers. It will be interesting to see whether this continues as we ease back into “exams as normal”.
Analysis by strand and topic
Despite some minor variations, pre and post-pandemic exam series have some similar and interesting patterns about the types of questions set and the complexity distribution for each topic, with some potential implications for exam preparation.
I have split the data set out into six strands, ‘Number’, ‘Algebra’, ‘Ratio and proportion’, ‘Geometry’, ‘Probability’ and ‘Statistics’, and added commentary on each strand below.
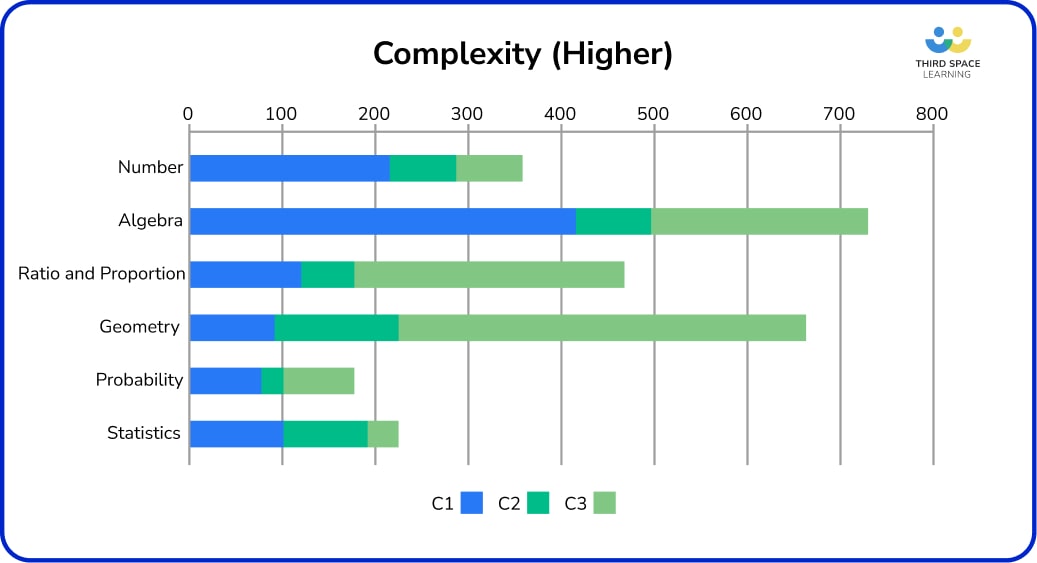
Before we get into the strand-by-strand analysis, it is interesting to look at patterns across the strands and papers as a whole.
Particularly of note:
- There is a higher proportion of C3 non-standard, context-based problems within Geometry, Probability, and Ratio and proportion.
- There is a higher proportion of C1 procedural problems in Number, Algebra and Statistics strands – however, there is less procedural Algebra than on Foundation.
- The highest proportion of C2 questions involving reasoning or interpretation occurs within Statistics.
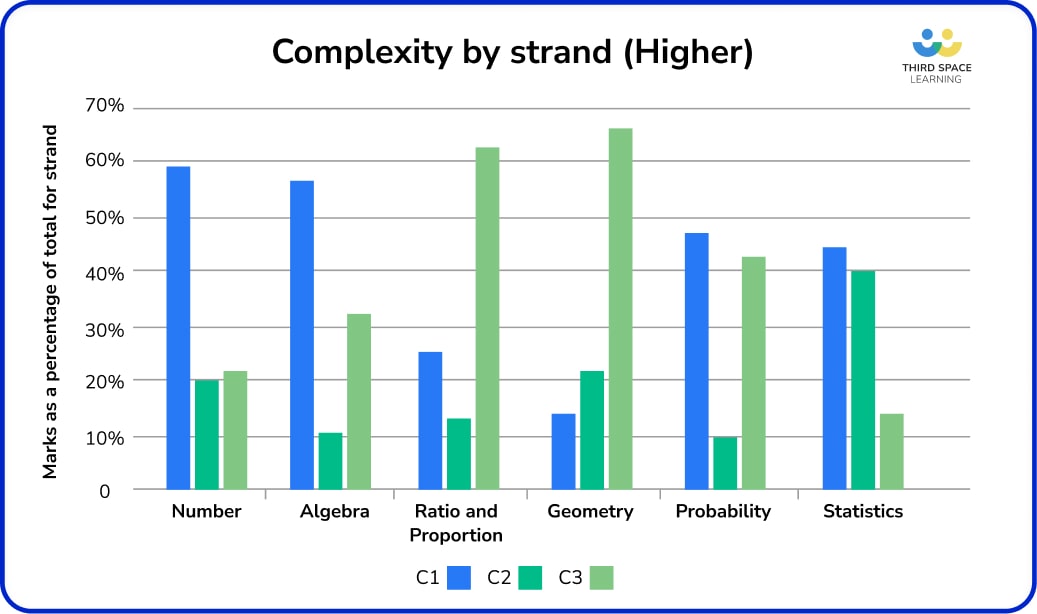
When preparing Higher groups for sitting exams, we can identify strands where more complex or unfamiliar problems are likely to occur (Geometry, Ratio and proportion, some Algebra) and invest more time in these.
It should be noted that the demand of the Algebra content in the maths course at Higher level is still high, even on procedural questions. A comprehensive grasp of basic algebra skills is fundamental for success at Higher.
Higher – number
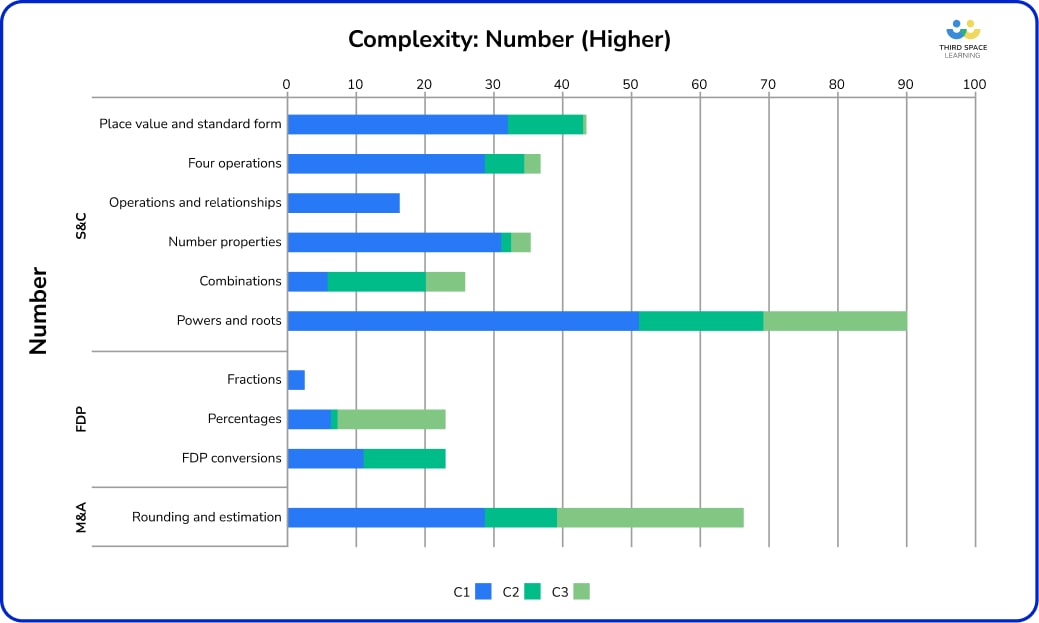
Compared to the Foundation paper, there is significantly less number work, particularly arithmetic, in the maths Higher past papers. Of the 19 marks available, 7 of these were for standard form (a mixture of C1 and C2 questions) and 7 for working with fractional indices, including one negative.
There was also significantly less work explicitly on proportional reasoning than on Foundation, although there were two C3 5 mark questions (P2Q2 and P3Q4) requiring candidates to solve problems using fractions, ratio, and percentages. The remaining 4 marks were for a fairly standard C1 inverse proportion equation: write the equation, then use this to find a value.
First of note is that there is still a significant proportion of procedural questions up for grabs in Number on Higher, particularly in Structure and Calculations. With the exception of a single question over the entire 11 series, place value and standard form was exclusively focused on the latter, with plenty of accessible C1 marks requiring candidates to convert to and from standard form, or carry out standard form calculations. C2 marks in this topic were for ‘show that’ type questions, spotting errors in presented working, or for explaining how a change to the calculation would affect the answer.
Four operations, factors, multiples and primes, and fraction calculations were nearly all C1. Although as noted above, these skills are also embedded throughout the maths Higher past papers. Most of the procedural fraction arithmetic questions involved mixed numbers. There was a mix of prime factorisation, HCF and LCM, and most of the work on four operations was on fraction or decimal calculations.
Rounding and estimation had a mix of types of rounding, but error intervals and bounds accounted for nearly 80% of the marks for Measures and Accuracy and appeared on nearly every series. There were a handful of rounding to decimal places and significant figures, usually as a follow-up to a use of calculator problem. Questions involving lower and upper bounds were likely to be assessed in context, and frequently included other embedded topics, such as compound measures.
Powers and roots attracted the greatest proportion of marks and has appeared on all 11 series so far. Nearly 60% of these marks were C1, and included working with fractional and negative indices, simple laws of indices and rationalising the denominator in surd questions. The C2 questions within this topic usually asked candidates to spot mistakes in a solution. Combinations was another topic that featured highly, also appearing on all 11 series so far.
All FDP conversions at Higher (excepting as an embedded skill in other topics) involved working with recurring decimals – either ordering or writing as a fraction. The C2 questions were ‘show that’ or ‘prove’.
What would I teach based on this data analysis?
- Basic calculation skills (four operations and working flexibly with fractions, decimals and percentages) need to be automatic.
- There is some accessible procedural work on standard form, HCF and LCM, negative and fractional indices, surd manipulation, expressing recurring decimals as fractions, using a calculator and error intervals, on most papers.
- Ensure students are familiar with systematic listing and combinations; it’s new to the 2015 specification, but features on every series so far.
Higher – algebra
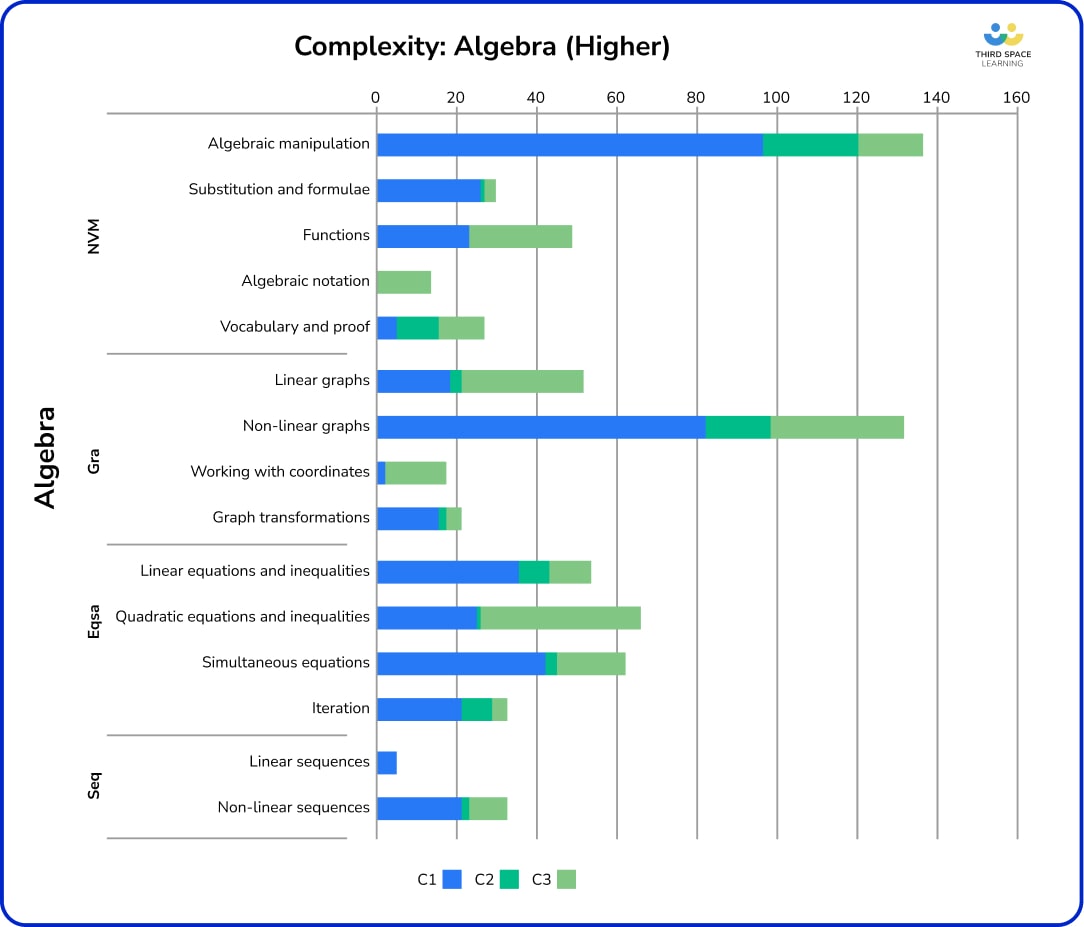
Algebra attracts a fair proportion of C1 and C3 marks, with relatively few C2. As expected, most applications topics have a higher proportion of C3 marks and these include:
- Linear graphs
- Non-linear graphs, particularly quadratics
- Working with coordinates (nearly all problem-solving on Higher)
- Quadratic equations and inequalities (context-based or embedded topics)
While algebraic manipulation is nearly 70% C1 procedural questions, candidates are also expected to be able to reason and solve problems using their algebra toolkit, particularly when applying these skills in related areas.
Nearly half of the marks in algebraic manipulation were for algebraic fractions; it’s worth noting that these questions also included things like expanding and factorising, including difference of two squares, so we can see that these basic skills are being assessed more commonly through work on algebraic fractions, rather than as standalone questions, as on Foundation.
Apart from algebraic manipulation, there was also a decent proportion of C1 marks available for the following topics:
- Linear equations and identities (much more likely in common questions)
- Simultaneous equations
- Iteration
- Sequences
- Substitution and formulae
Note that some of these are typically considered more difficult topics. For example, C1 simultaneous equations questions were just as likely to be about non-linear systems as the “standard” two linear. The questions on iteration were done step-by-step, were generally procedural and followed a set pattern, so could be easier marks to pick up.
Note that linear and quadratic equations were frequently examined in other C3 contexts, particularly perimeter, area and volume or shape and angle properties.
Graph work, both linear and non-linear, had a fair proportion of C3 problems; these were generally multi-step coordinate geometry problems, similar to those seen at early A Level, rather than applications to other topics. That said, over 60% of the marks on non-linear graphs were available on C1 questions, including drawing graphs of quadratics and circles, matching graphs with equations (this style of question appeared on half of the series so far), and estimating solutions to equations from graphs.
What would I teach based on this data analysis?
- Basic algebra skills (simplify, expand, factorise, solving equations and inequalities) need to be automatic. Algebraic fractions are frequently used to assess a range of algebraic manipulation skills.
- Linear and quadratic equations and inequalities are frequently assessed in a variety of contexts, particularly perimeter, area and volume.
- There is some accessible procedural work within sequences, functions, such as quadratic nth term, inverse and composite functions, basic graph skills, equation of a straight line, drawing graphs and estimating solutions from a graph.
- Other key topics include: simultaneous equations, including non-linear, expanding triple brackets, solutions of equations using iteration, gradients and areas, particularly using speed-time and distance-time graphs.
Higher – ratio and proportion
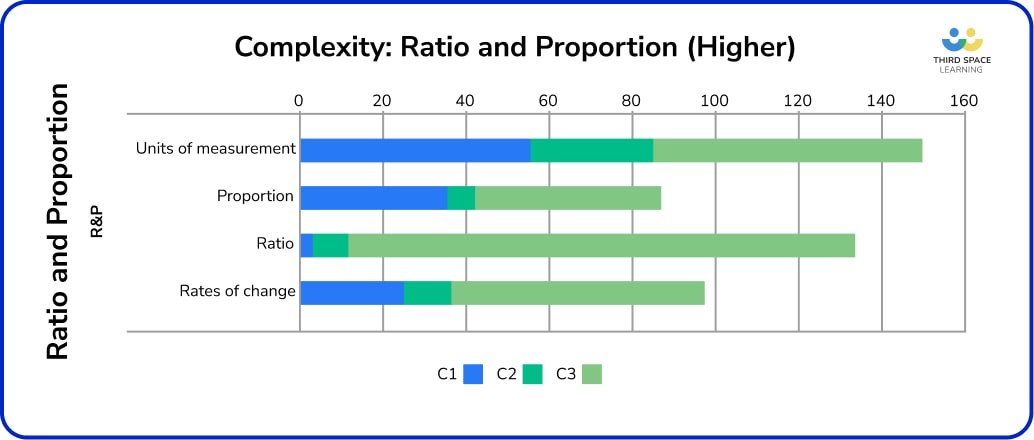
Similarly to Foundation, a large percentage of Ratio and Proportion questions were classified C3 (problem-solving). This is particularly evident with work on ratio at Higher. For example, there were no questions asking candidates to simply ‘split into a ratio’, as this was assessed through other topics by presenting key question information as a ratio.
It should also be noted that ratio is also one of the topics that is most frequently embedded in other questions (see June 2019 1H Q17 for an example of solving a quadratic with a ratio).
Key topics in percentages were:
- Compound interest and other repeated change
- Reverse percentages
- Percentage profit
- Use of exponential notation to represent repeated change
Most of these were presented in real-life contexts, such as depreciation of price or money in a bank account.
Compound measures accounts for well over half of the marks for units of measurement, and nearly 20% of the entire strand. The topic has appeared on every series so far, and is a favourite topic for common questions, appearing at the start of the Higher paper. Density frequently appears in combination with volume of 3D shapes.
Nearly a third of the marks in units of measurement are for distance or speed-time graphs, with a high frequency of appearances per series. Questions in this topic and on other real-life graphs are more likely to be asked procedurally.
What would I teach based on this data analysis?
- Proportional reasoning, particularly ratio, is assessed throughout the paper, and lack of understanding could limit accessibility of other topics. Ensure a strong understanding of direct and inverse proportion, and fluency with ratio skills.
- Explicit teaching and modelling of problem-solving in the real-life contexts presented in percentage questions.
- There should be plenty of applied work with compound measures, including interweaving with other topics such as volume and surface area.
Higher – geometry
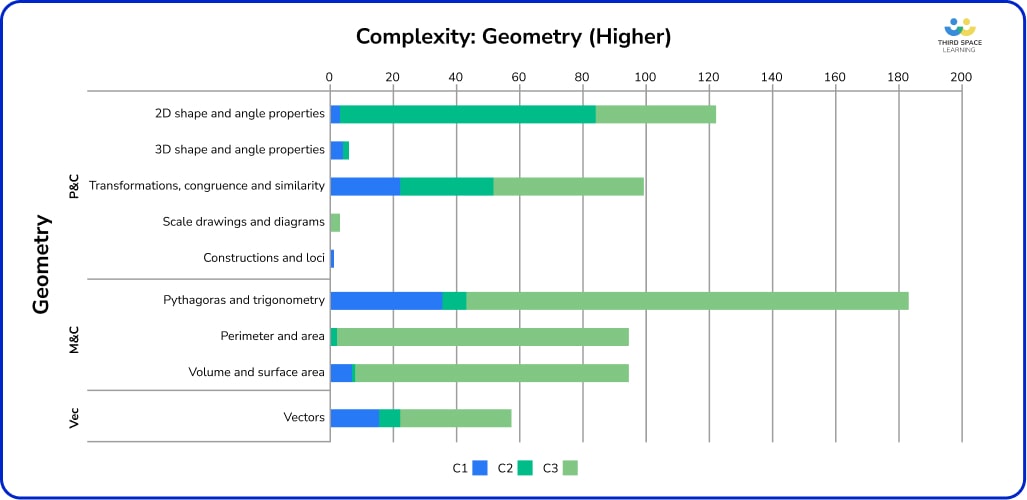
Similar to the Foundation papers, the maths Higher past papers featured a heavy emphasis on C3 applications within Measures and Calculations, particularly in perimeter, area, volume and surface area. I was also surprised at the high proportion of C3 problems on Pythagoras and trigonometry.
Candidates were unlikely to be presented with a simple right-angled triangle problem to solve using Pythagoras or trigonometry. Questions involving simple applications of trigonometry often had information presented in a non-standard way, such as giving angles as ratios rather than values.
Nearly 80% of Higher level trigonometry, such as sine and cosine rule problems, was C3. Many of these questions required a double application of sine/cosine rule, or use of Pythagoras, or some crossover with area calculations. 3D Pythagoras or trigonometry appeared on just over half of the series.
Perimeter, area and volume was nearly all assessed in an applied manner, with some series having all of this topic assigned C3. There were fewer real-life contexts than on Foundation, but problems requiring multiple steps, such as calculating a volume given a surface area, or vice versa, featured highly. There are very few simple questions asking candidates to calculate an area or volume, possibly because many formulae, particularly for volume and surface area, are given.
Transformations had a Higher percentage of C1 marks available than many other Geometry topics; enlargements appeared more frequently than any of the other three transformations. The C2 marks within this topic were mostly for describing transformations, so were also fairly accessible.
2D shape and angle properties attracted the highest proportions of C2 marks, purely because many of the questions in this topic contain the statement: ‘give reasons for your answer’. The most commonly assessed topics here were circle theorems and interior and exterior angles in polygons.
It’s worth noting the very low proportion of work at Higher level on constructions, loci, scale drawing and bearings – so far constructions have only appeared procedurally once across eleven series.
What would I teach based on this data analysis?
- Explicit teaching of problem-solving skills when working on perimeter, area and volume, including links to other topics such as linear and quadratic equations and inequalities.
- When teaching Pythagoras and trigonometry, increase focus on problem-solving or multi-step problems requiring applications of more than one rule, working in 3D or applying to area calculations.
- Ensure that candidates can give clear mathematical reasoning for 2D shape and angle problems, particularly angles in polygons and circle theorems.
Higher – probability
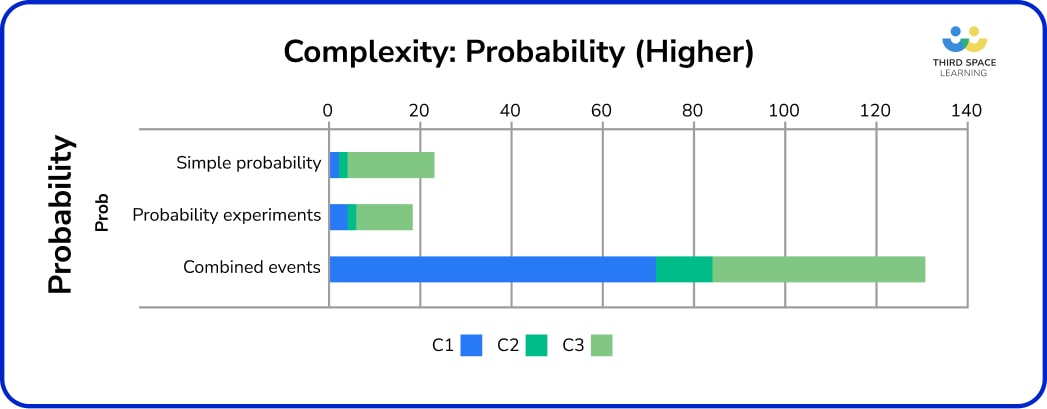
Over the eleven series of maths Higher past papers, the ‘new content’ (i.e. added in 2015) is strongly represented in the Probability strand. Unlike Foundation, there were no questions with pre-drawn frequency trees (although candidates could have chosen to use these for non-structured questions), with focus almost exclusively on tree diagrams. Venn diagrams and combinations featured highly, appearing on most series.
Looking at the strand as a whole, there was a fairly even split of procedural C1 and more challenging C3 problems. However, the majority of the procedural questions appeared in combined events, with more procedural work in simple probability and probability experiments.
C3 questions included a non-structured problem lending itself well to Venn diagrams (June 18 P3Q20), and a problem requiring ratio calculations in addition to probability (June 18 P1Q16). As on Foundation, mutually exclusive events were most likely to be examined at C3.
What would I teach based on this data analysis?
- Look for accessible procedural work on Venn diagrams and tree diagrams.
- Ensure that students can apply fraction and ratio skills to unfamiliar contexts for mutually exclusive events or relative frequency.
- Extend higher-attaining students with plenty of practice with combined event problems.
Higher – statistics
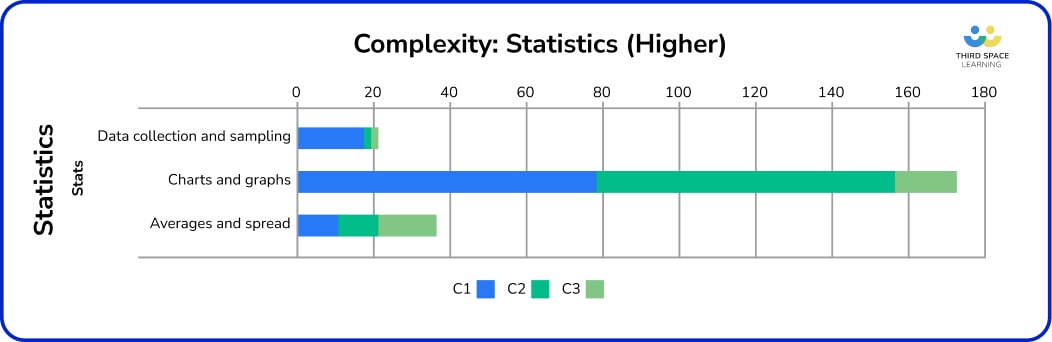
As with Foundation, the majority of statistics content is C1 and C2, although there is slightly more problem-solving expected at Higher. Averages and spread attracted the greatest proportion of C3 marks; nearly two-fifths of the marks in this strand were for problem-solving, with questions involving the mean featuring particularly highly.
Over three-quarters of the statistics marks were for charts and graphs. A large proportion (44%) of presenting data is C2, meaning that candidates are almost as likely to be asked to analyse, read information from or critique a graph or chart as they are to draw one. Cumulative frequency charts, box plots, histograms and frequency polygons appeared most frequently, with some work on time series graphs and pie charts.
In averages and spread, nearly a third was C2 which this tends to be reading or estimating averages or range from given tables or charts. 32% of the marks for averages and spread were C1, and these were almost exclusively for estimating the mean or finding the median class interval from a table, and nearly always appeared in common questions.
Sampling was assessed on half of the series so far; it appeared in June 2019 (P2Q3) and November 2019 (P2Q4) in an almost identical format with a ‘stratified sample-style’ question. Capture-recapture has appeared on three of the six most recent series.
What would I teach based on this data analysis?
- Maximise marks on charts and graphs, particularly cumulative frequency, box plots, frequency polygons and histograms.
- Ensure that students can solve problems using the mean, including finding missing amounts.
- Make sure all students are familiar with calculating averages and spread for grouped data.
Frequently occurring topics – common questions
This section of the article focuses the questions that appear on both tiers: the common or crossover questions. These are the first few questions of the Higher papers and, as such, this is material that the average Higher candidate should find fairly accessible.
On average, we’re looking at around 20-25 questions per series, split over three papers – this averages to approximately 8 common questions per paper, which are often split into parts. As these carry nearly a third of the overall marks per paper, it’s crucial that Higher students pick up every mark that they can in this part of the paper. This section contains some suggestions for doing this.
When students sat the first series for the new specification in 2017, Edexcel were criticised for the difficulty of content in the common questions, and adaptations were made to the papers to account for this from June 2018. Due to these changes, I have omitted June and November 2017 papers from this section of the analysis.
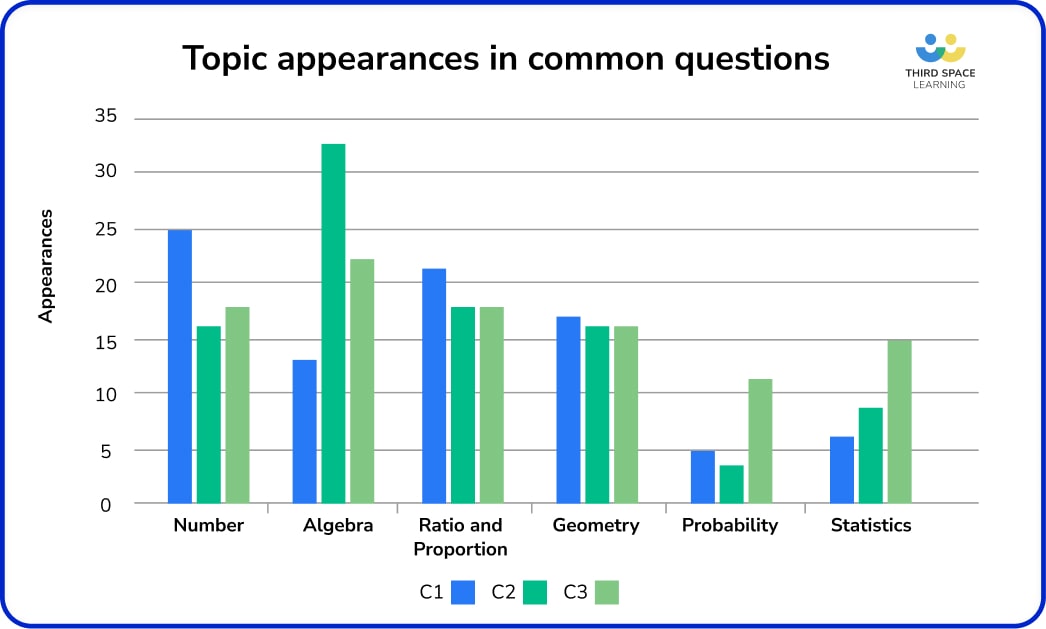
On this graph, part questions are counted as separate appearances to account for different topics assessed in different parts of questions.
Key points
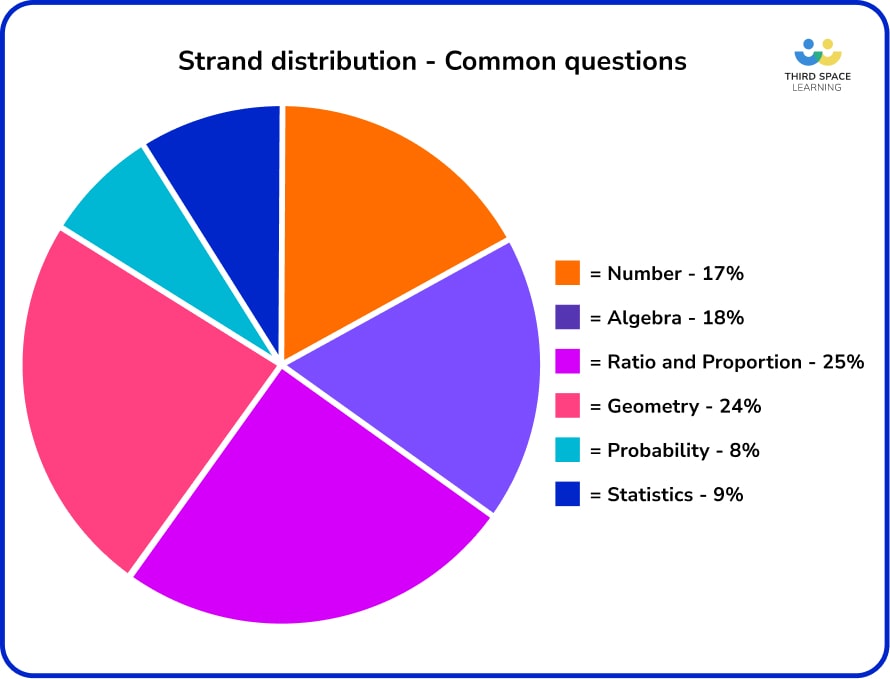
- The proportion of Number content is greater on Paper 1 (non-calculator), following the pattern for the rest of the papers at both tiers. For example, Number is assessed more frequently on the non-calculator paper.
- Strand distributions generally follow the pattern for the rest of the Higher papers, although there is slightly more Number and Ratio and proportion in the common questions.
- There is lots more Probability and Statistics on Paper 3 than on the other two papers – this is probably a curiosity rather than by deliberate design, as the content on Papers 2 and 3 (calculator papers) should be functionally identical.
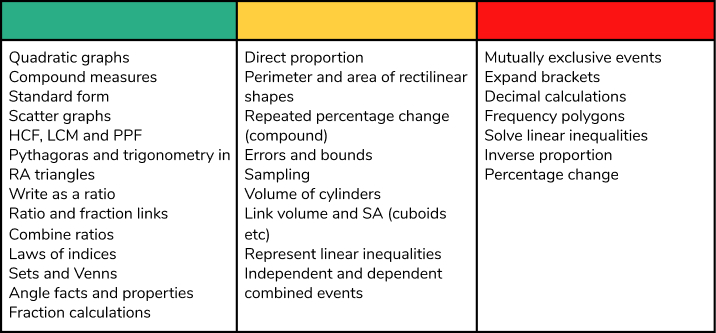
Frequently occurring topics
As we’d probably expect, some topics appear much more frequently than others in common questions. Although this shouldn’t be used to narrow down taught content, it does perhaps give an indication of where to focus final Higher revision when time is tight.
This table contains topics with three or more appearances in common questions from June 2018 onwards.
Topics that attract the most marks
There are some topics for common questions that are worth more marks on average. Note that there is quite a lot of crossover between the topics in this list and the one above, as topics which appear more frequently per series will usually have a higher average mark per series. Here is the list of twenty common question topics worth the most marks:
- Speed, distance, time
- Ratio and FDP problem solving
- Compound interest and depreciation
- Angles in polygons
- Plot graph of quadratic function
- Venn diagrams
- Convert numbers in standard form
- Simple laws of indices
- Find missing sides and angles using trigonometry
- Problem solving using perimeter and area
- Multiply and divide decimals
- LCM
- Combine ratios
- Find roots and estimate solutions from quadratic graph
- Percentage increase and decrease
- Add and subtract fractions
- Multiply and divide fractions
- Find percentages of amounts
- Error intervals
- Draw and use scatter graphs
Frequently occurring topics – first half
In this section of the article I look at the most frequently occuring topics in the earlier questions on the Higher papers, excluding the common questions. For Higher students aiming for a grade 6, these are a good place to pick up a decent proportion of marks. Students aiming for higher grades should be fluent in this content.
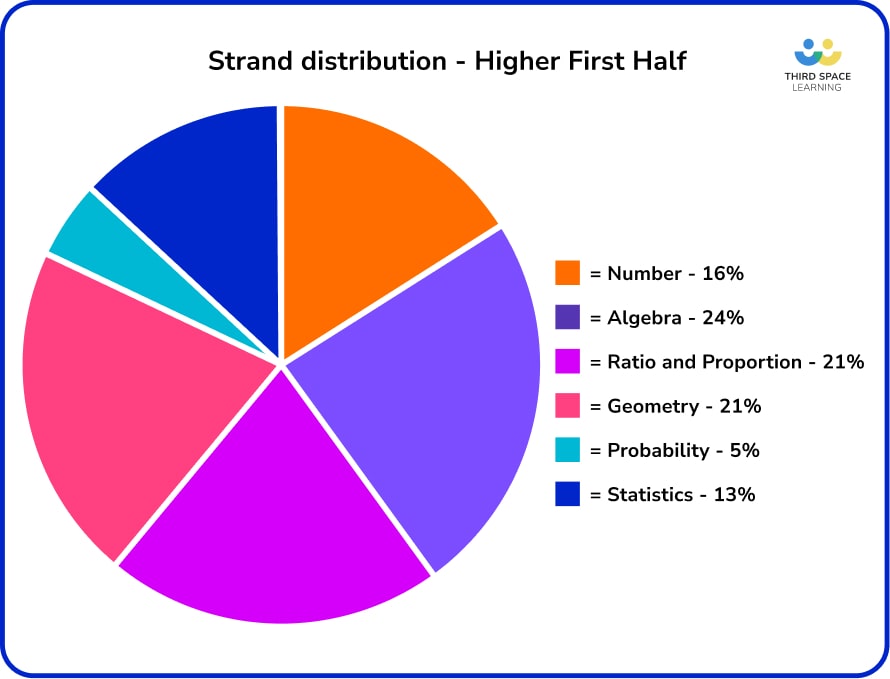
Key takeaways
- There is slightly more Statistics and slightly less Algebra and Probability in this section of the paper
- Generally, strand distributions follow the rest of the paper.
Frequency of topics in the first half of the paper (common questions excluded)
This table shows the topics that have had three or more appearances so far in the first fifteen questions of the Higher Edexcel papers, traffic-light coded to indicate frequency of appearance. Common questions have been excluded, but note that some of these topics are also assessed in common questions.
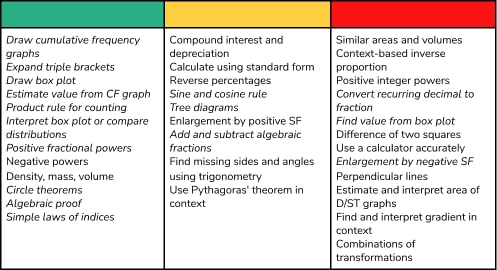
When averaged out per paper, there are just over 50 marks on the first fifteen questions (including common questions) on Higher. On most series, this is more than enough to achieve a grade 7.
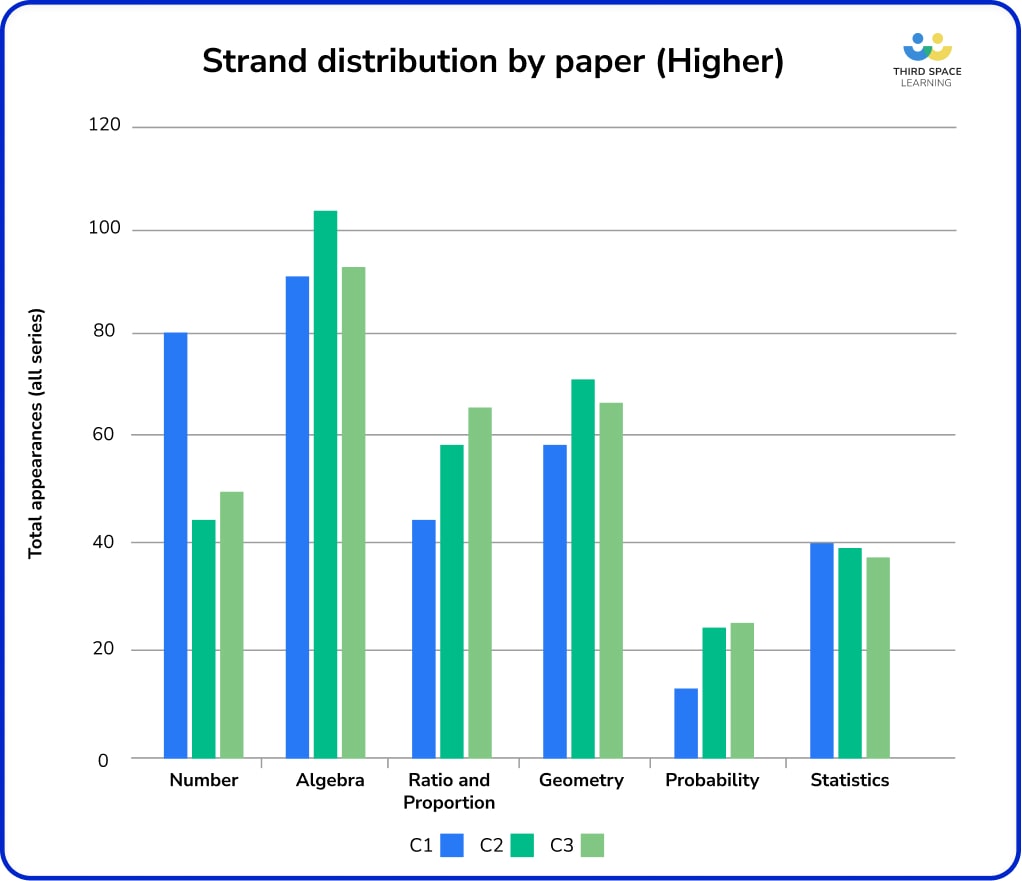
Paper 1 higher topics
At GCSE, Paper 1 is a non-calculator paper, whereas Papers 2 and 3 allow the use of a calculator. This impacts which topics are more likely to appear on Paper 1, or on Papers 2 and 3.
Broadly speaking:
- Paper 1 is significantly more arithmetic and calculation intensive.
- Number topics are twice as likely to appear on Paper 1 as on Papers 2 and 3 (this is a greater skew than Foundation).
- There are slightly fewer questions on Ratio and proportion, Geometry and Probability on Paper 1.
- Topics which don’t require a calculator (transformations, drawing and interpreting charts and graphs, constructions and loci) are more likely to appear on Papers 2 or 3, simply because there’s less room for them on Paper 1.
Topics with a high proportion of appearances on paper 1
This table lists topics with three or more appearances on paper 1. Note that any topic could theoretically appear on any paper, and many of these topics also feature highly on papers 2 and 3.
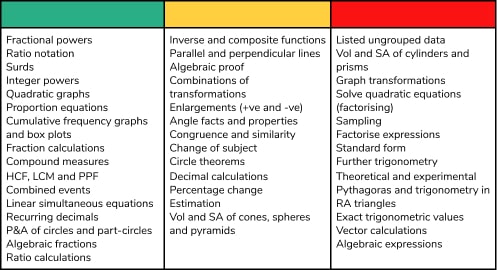
Topics with no significant appearance on paper 1 (so far!)
This list contains topics that have not appeared on any Edexcel Foundation Paper 1 (2017-2023). Please note that some of the topics on this list have had very few appearances overall, or are rarely assessed at Higher level anyway.
Final thoughts from this analysis of Edexcel maths higher papers
Analysing the new specification GCSE Higher papers has been very interesting. It caused me to re-evaluate some of the ideas I had about exam preparation, what topics it is appropriate to focus on with each group, and to think further about time weightings given to certain topics once GCSE maths revision begins.
One of the goals for GCSE maths 2015 was to increase the number of multi-topic questions requiring students to make mathematical connections and apply their skills to unfamiliar contexts. This messaging from Ofqual and exam boards has been emphasised with the publication in July 2023 of Ofsted’s Coordinating Mathematical Success, which discusses the importance of teaching problem-solving skills in some detail.
Teaching problem-solving cannot be done as a quick fix at the end of a syllabus; it should be allocated time in a scheme of work and connected to learning. For example, when teaching density or pressure, give students plenty of problems requiring the application of formulae for volume or surface area.
Teaching problem-solving cannot be done as a quick fix at the end of a syllabus; it should be allocated time in a scheme of work and connected to learning. For example, when teaching density or pressure, give students plenty of problems requiring the application of formulae for volume or surface area.
However, with regard to final exam preparation, there are some considerations when looking at the frequency at which some topics appear on Higher papers, or whether certain harder topics are likely to be assessed procedurally. For example, quite a lot of Number content at Higher is still assessed procedurally, so there is potentially less value in spending a lot of vital exam preparation time on rich problems within Number topics – this would be better assigned to tackling context-based problems in Ratio and proportion, or applying algebra skills to geometric problems.
For students aiming for a grade 6 or lower, careful focus on those topics most likely to appear in the crossover content, or in the rest of the first half of the paper, is a prudent use of revision time, baring in mind that students to complete a significant amount more work per mark on the final few questions on the paper. For these candidates, emphasis should be on maximising marks and checking for errors on the first two-thirds or so of the paper, rather than trying to “get through” the whole paper.
For further suggestions on how you can use this analysis to impact your teaching of Higher exam groups, see the companion piece on higher topics essential to GCSE success this year.
READ MORE
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online GCSE maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the GCSE revision programme or request a personalised quote for your school to speak to us about your school’s needs and how we can help.