One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Fractions, decimals and percentages Decimals Fractions Probability notation Frequency trees Venn diagramsThis topic is relevant for:

Probability Formula
Here we will learn about probability formula, including mutually exclusive events, independent events and conditional probability.
There are also probability of events worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is probability formula?
Probability formula is used to calculate the probability of single and multiple events. Probabilities are values that show the likelihood of an event.
Finding the basic probability of event A happening can be calculated using the formula
P(A)=\cfrac{\text{number of times A occurs }}{\text{total number of possible outcomes}} ,
where P(A) is the notation used to mean “the probability of A happening”.
If the probability needed is more complicated and involves multiple events we need to consider if the events satisfy conditions such as being mutually exclusive or independent.
What is probability formula?

Probability of an event not happening
The total probability of all events happening is 1 or 100 \%.
If we want to calculate the probability of an event not happening we can use the formula
P(\operatorname{not} A)=1-P(A).
This can also be written as
P\left(A^{\prime}\right)=1-P(A),
where A^{\prime} refers to the complement of A or “not A”.
For example,
The probability of it raining on Monday is 0.3.
What is the probability of it not raining on Monday?
P(\text{not raining on Monday})=1-0.3=0.7Mutually exclusive events
Mutually exclusive events can be thought of as disjoint events. They cannot happen at the same time.
For example,
When rolling a single fair die, rolling an odd number is mutually exclusive to rolling an even number.
When we have mutually exclusive events, A and B, we can use the formula
P(A \text { or } B)=P(A)+P(B).
For example,
The probability of rolling a 2 or an odd number on a fair die,
P(2 \text { or odd})=P(2)+P(\text {odd})=\cfrac{1}{6}+\cfrac{3}{6}=\cfrac{4}{6}.
As 2 is an even number and not odd, these two events are mutually exclusive.
However, if we wanted to calculate the probability of rolling an odd number or a prime number, these events are not mutually exclusive so we cannot add the individual probabilities.
The numbers 3 and 5 are odd and prime.
To calculate the probability of rolling an odd number or a prime number it helps to use a sample space diagram or a Venn diagram.
For example,
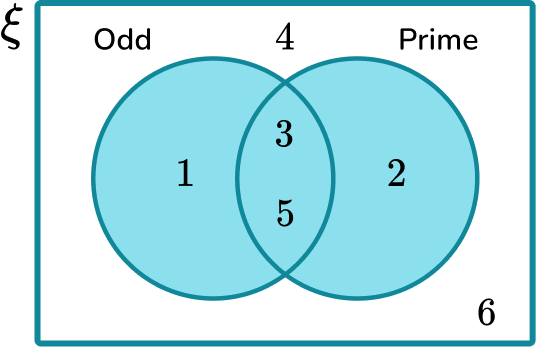
The Venn diagram shows the two sets, odd numbers and prime numbers.
To calculate P(odd or prime) we need the union of the two sets.
The union of two sets is shown using the \cup symbol, this has been shaded in the Venn diagram below.
P(\text { odd } \cup \text { prime })=\cfrac{4}{6}
We may also see mutually exclusive events displayed in a probability distribution.
For example,
This probability distribution shows the probabilities of a 4 -sided spinner landing on the numbers 1 to 4.
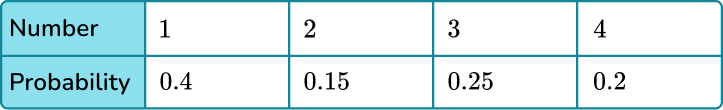
The probabilities listed in a probability distribution can be based on theoretical probability or experimental probabilities that come from calculating the relative frequency of an event occurring during an experiment.
The formula for relative frequency is
\text{Relative frequency = }\cfrac{\text{frequency of event occurring}}{\text{total number of trials of the experiment}}.
Independent events
Independent events are events which are not affected by the occurrence of other events.
If we roll a die twice, the outcome of the first roll and second roll have no effect on each other – they are independent events.
For independent events, P(A \text { and } B)=P(A) \times P(B) .
For example,
The probability of flipping a coin twice and it landing on heads both times,
P(\text {Head and Head})=P(\text {Head}) \times P(\mathrm{Head})=\cfrac{1}{2} \times \cfrac{1}{2}=\cfrac{1}{4}.
Dependent events
When events are dependent we cannot multiply the probability of two separate events together.
We need to consider the probability of the second event given that the first event happened.
This is known as conditional probability.
To calculate probability of event B given event A, we can use Venn diagrams or tree diagrams.
For example,
Charlie has a bag of sweets. There are 5 yellow sweets and 4 red sweets.
Charlie is going to take a sweet at random, eat it and then take a second sweet to eat.
To calculate the probability of Charlie eating a sweet of each colour we can display the probabilities on a tree diagram.
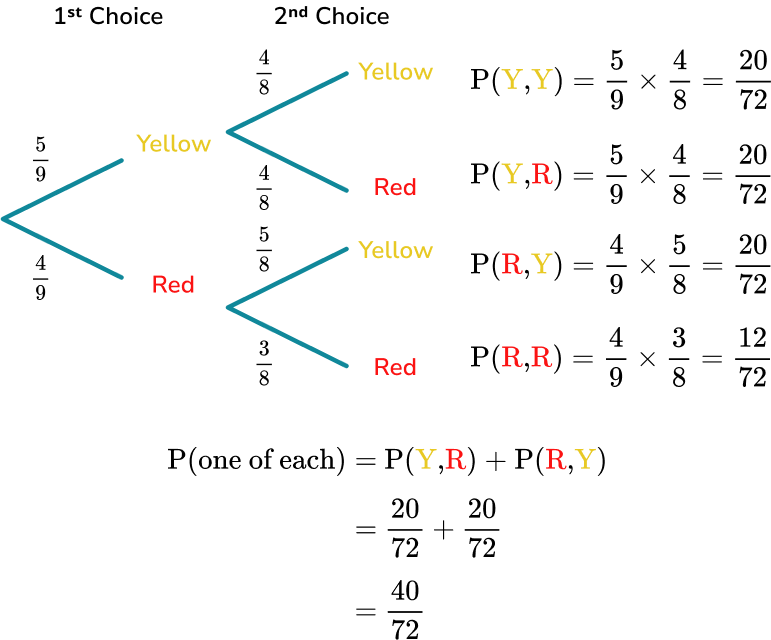
You can see that the probabilities on the second set of branches are different from the probabilities on the first set and to each other. This is because the probabilities of choosing the second sweet depend on the colour of the previous sweet.
Links to A Level Maths
In A Level Mathematics we learn about the conditional probability formula
P(A \text { given } B)=\cfrac{P(A \text { and } B)}{P(B)}.
We can see how this works using a Venn diagram.
For example,
The Venn diagram shows the number of students in a college that study Maths or English or both.
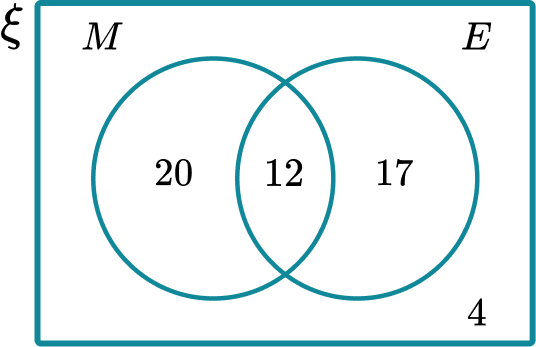
Finding the probability of an English student also studying Maths, is the same as finding the fraction of the English students that study Maths.
The intersection M \cap E are the students that study Maths and English.
There are 12 students that study both Maths and English. 29 students in total study English.
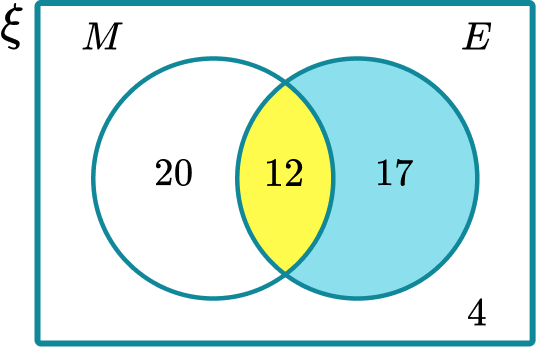
So the probability of an English student also studying Maths is
\cfrac{P(\text {Maths and English})}{P(\text {English})}=\cfrac{12}{29}.
In A Level Mathematics we also learn the addition rule of probability which is true for events that are not mutually exclusive.
P(A \text { or } B)=P(A)+P(B)-P(A \text { and } B)
If A and B are mutually exclusive, P(A \text { and } B)=0 and the formula becomes
P(A \text { or } B)=P(A)+P(B).
A Level Mathematics also covers a lot more probability theory such as binomial distributions and normal distributions.
How to use probability formula
In order to use a probability formula:
- Decide if the probability is for a single event or multiple events.
- Choose the correct formula to use.
- Calculate the probability as a fraction, decimal or percentage.
How to use probability formula


Probability of events worksheet (includes probability formula)

Get your free probability formula worksheet of 20+ probability of events questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Probability of events worksheet (includes probability formula)

Get your free probability formula worksheet of 20+ probability of events questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEProbability formula examples
Example 1: probability of a single event happening
Each letter of the alphabet is written on a card and the cards are shuffled.
Find the probability of randomly selecting a vowel.
- Decide if the probability is for a single event or multiple events.
This represents a single event.
2Choose the correct formula to use.
We will use the basic probability formula
P(A)=\cfrac{\text { number of times } A \text { occur }}{\text { total number of possible outcomes }} .
3Calculate the probability as a fraction, decimal or percentage.
There are 5 vowels in the alphabet.
P(\text {vowel})=\cfrac{5}{26}
Example 2: probability of not A
The probability of a bus being late on Tuesday is 0.15.
What is the probability of the bus not being late?
Decide if the probability is for a single event or multiple events.
This represents a single event.
Choose the correct formula to use.
We can use the formula for P(\operatorname{not} A).
P\left(A^{\prime}\right)=1-P(A).
Calculate the probability as a fraction, decimal or percentage.
\begin{aligned}& P(\text {late})=0.15 \\\\ & P(\text {not late})=1-0.15=0.85\end{aligned}
Example 3: probability of event A or B happening
A fair dice is rolled. Find the probability of it landing on a 2 or a 3.
Decide if the probability is for a single event or multiple events.
This represents two events, either landing on a 2 or a 3.
Choose the correct formula to use.
The two events are mutually exclusive so we can use
P(A \text { or } B)=P(A)+P(B).
Calculate the probability as a fraction, decimal or percentage.
\begin{aligned}P(2 \text { or } 3) & =P(2)+P(3) \\\\ & =\cfrac{1}{6}+\frac{1}{6} \\\\ & =\cfrac{2}{6}\end{aligned}
Example 4: probability of event A and B happening
Kelly plays a game of badminton and a game of squash. The probability that she wins badminton is 0.7. The probability that she wins squash is 0.6.
Find the probability that she wins both games.
Decide if the probability is for a single event or multiple events.
This represents two events, winning badminton and winning squash.
Choose the correct formula to use.
The two events are independent so we can use
P(A \text { and } B)=P(A) \times P(B).
Calculate the probability as a fraction, decimal or percentage.
\begin{aligned}P(\text {wins badminton and wins squash}) & =P(\text {wins badminton}) \times P(\text {wins squash}) \\\\ & =0.7 \times 0.6 \\\\ & =0.42\end{aligned}
Example 5: probability of event B given A
The two-way table shows information about year 10 and year 11 pupils studying languages.
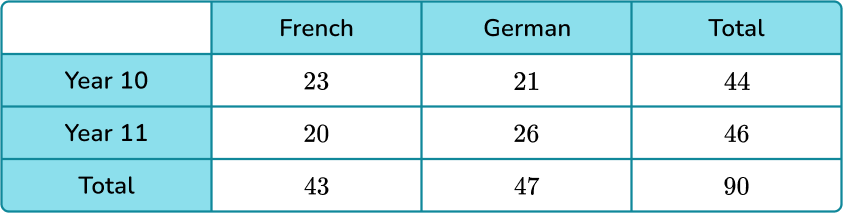
A year 11 student is selected at random. Find the probability that they study French.
Decide if the probability is for a single event or multiple events.
This represents two events, being in year 11 and studying French.
Choose the correct formula to use.
This is a conditional probability. We need to look at the fraction of year 11 students that study French or we can use the formula
P(A \operatorname{given} B)=\cfrac{P(A \text { and } B)}{P(B)}.
Calculate the probability as a fraction, decimal or percentage.
Thinking about the fraction, there are 20 year 11 students that study French out of 46 year 11 students in total.
This will give as a fraction of \cfrac{20}{46}.
Alternatively using the formula,
\begin{aligned}P(\text {study French given year } 11) & =\cfrac{P(\text {study French and year } 11)}{P(\text {year } 11)} \\\\ & =\cfrac{\cfrac{20}{90}}{\cfrac{46}{90}} \\\\ & =\cfrac{20}{46}\end{aligned}
Example 6: calculating a relative frequency
A 4 -sided spinner is spun several times in an experiment and the table shows the number of times it landed on each number.
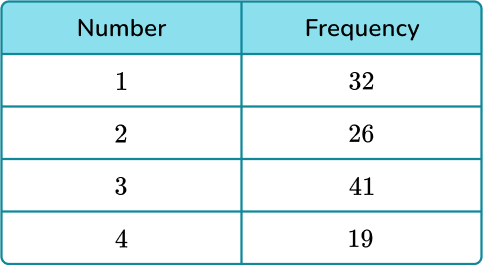
Using the information, calculate the probability of the spinner landing on the number 1. Give your answer as a decimal to 3 decimal places.
Decide if the probability is for a single event or multiple events.
This represents a single event.
Choose the correct formula to use.
We will use the relative frequency formula.
\text{Relative frequency = }\cfrac{\text{frequency of event occurring}}{\text{total number of trials of the experiment}}.
Calculate the probability as a fraction, decimal or percentage.
We know the spinner landed on the number 1, 32 times. We need to know the total number of times the spinner was spun.
32+26+41+19=118
P(1)=\cfrac{32}{118}=0.271 (3 d.p.)
Common misconceptions
- Adding probabilities instead of multiplying them
For independent events P(A \text { and } B)=P(A) \times P(B).
For mutually exclusive events P(A \text { or } B)=P(A)+P(B).
- Not changing the probability for the second pick when picking two objects (conditional probability)
If a bag contains 6 milk chocolates and 6 dark chocolates. The probability of selecting a milk chocolate at random is \cfrac{6}{12} or \cfrac{1}{2}. If that chocolate is eaten and another selected, the probability of choosing another milk chocolate is no longer \cfrac{6}{12} or \cfrac{1}{2} , it is now \cfrac{5}{11}.
- Probabilities being greater than \bf{1}
The total probability of all possible events will add to 1. If you are finding a probability for combined events and get an answer greater than one you need to check for any mistakes in your method.
Practice probability formula questions
1. Which formula would you use to find the probability of A or B when A and B are mutually exclusive events?




To find the probability of A or B when A and B are mutually exclusive events you add the two probabilities.
2. The 5 -sided spinner can land on the letter A, B, C or D
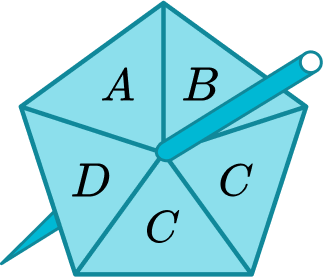
What is the probability it will land on A or C?




To find the probability of A or C when A and C are mutually exclusive events you add the two probabilities.
\cfrac{1}{5}+\cfrac{2}{5}=\cfrac{3}{5}
3. A fair coin is flipped and a fair 6 -sided die is rolled.
What is the probability of obtaining a head and a 3 ?




For independent events P(A \text { and } B)=P(A) \times P(B)
\cfrac{1}{2}\times \cfrac{1}{6}=\cfrac{1}{12}
4. The probability that Manny wins a game of tennis is 0.65.
What is the probability of Manny not winning?




P(\text {not } A) = 1-P(A)
P (\text{Manny not winning})=1-0.65=0.35
5. The Venn diagram shows information about the subjects a group of 80 students study.
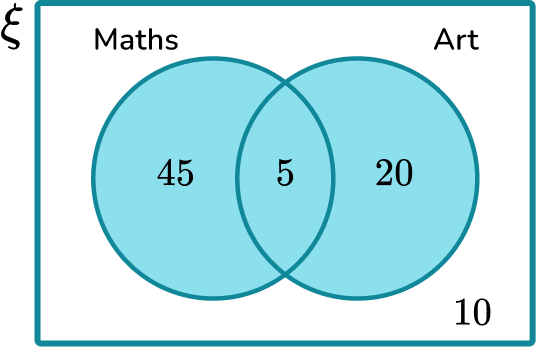
A student is selected at random. Given that they do not study maths, what is the probability that they study art?




We need the fraction of students who do not study maths that study art. 30 students do not study maths, out of them, 20 study art.
6. A die was rolled 50 times and it landed on a 2 on 12 occasions.
Use the information to write a probability of the die landing on a 2.




We need to calculate the relative frequency of the die landing on a 2.
\text{Relative frequency = }\cfrac{\text{frequency of event occurring}}{\text{total number of trials of the experiment}}
\cfrac{12}{50}=0.24
Probability formula GCSE questions
1. The probability of it snowing in December is 0.32. What is the probability of it not snowing?
(2 marks)
1-0.32
(1)
0.68
(1)
2. The table shows the probability distribution for a four-sided spinner.
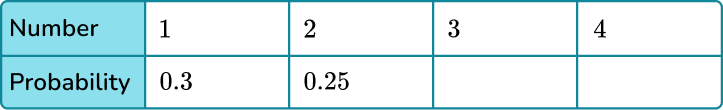
The probability of the spinner landing on a 3 is four times more likely than it landing on a 4.
(a) Complete the table for the probabilities of the spinner landing on a 3 and on a 4.
(b) Calculate the probability of the spinner landing on an even number.
(5 marks)
(a)
0.45
(1)
Attempt to find one fifth of 0.45 or split in a ratio of 4\text{:}1.
(1)
P(3)=0.36, P(4)=0.09
(1)
(b)
0.25+0.09
(1)
0.34
(1)
3. A bag contains 6 red counters and 3 blue counters.
Adam is going to select two counters from the bag at random.
What is the probability Adam selects one of each colour?
(3 marks)
\cfrac{6}{9} and \cfrac{3}{9}.
(1)
\cfrac{6}{9}\times \cfrac{3}{8} + \cfrac{3}{9}\times \cfrac{6}{8}
(1)
\cfrac{36}{72} or equivalent.
(1)
Learning checklist
You have now learned how to:
- Calculate basic probabilities
- Calculate the probability of two events happening
- Calculate the probability of mutually exclusive events
- Calculate the probability of independent events
- Deal with conditional probability
- Solve probability problems
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.