One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Probability scale Probability notation Fractions, decimals and percentagesThis topic is relevant for:

Describing Probability
Here we will learn about describing probability, including describing probability using words, recognising the likelihood of an event and placing events on a probability scale.
There are also describing probability worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is describing probability?
Describing probability is when we make judgements as to whether an event will take place. To do this we use words to describe how probable the event is.
For example,
We may say that it is likely to rain tomorrow, or that it is impossible for the sun not to rise.
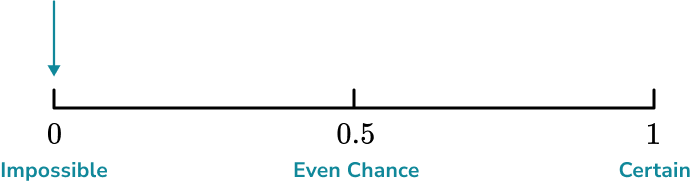
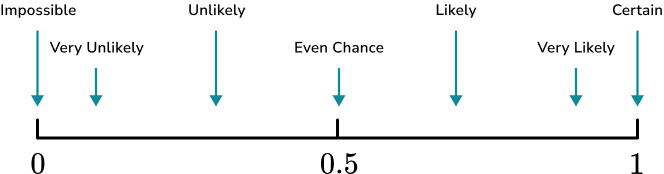
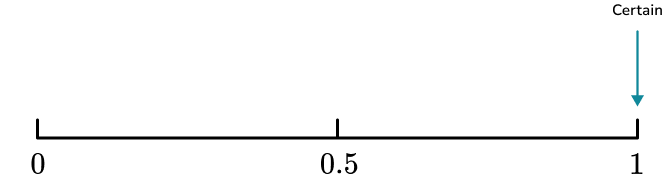
Some other common words used to describe the probability of an event happening include; certain, very likely, even chance, unlikely and very unlikely.These words can be placed on a probability scale starting at 0 (impossible) and ending at 1 (certain).
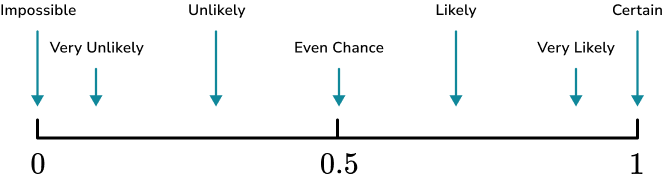
What is describing probability?

Probability scale
The probability scale is used to represent probabilities on a number line from 0 to 1. In maths, we more often than not use numbers to describe probabilities. Hence, the probability scale starts at 0 (impossible) and ends at 1 (certain).
You could also be asked to place events on a probability scale. To do this you need to consider the words suitable to describe the probability of the event happening, or the number which would represent the chance of the event happening.
For example,
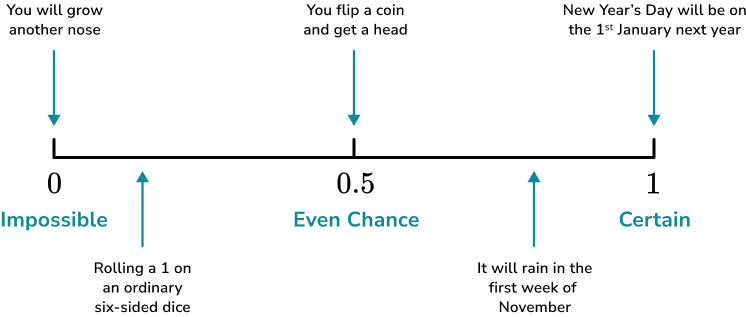
Step-by-step guide: Probability scale
Probability symbol
Probability symbols are used to write mathematical statements describing probability. These symbols allow us to shorten a mathematical statement to make it more clear and concise. These symbols will also be seen in set notation when using Venn diagrams to represent information.
For example,
Here are the key set notation used in probability, along with their descriptions.
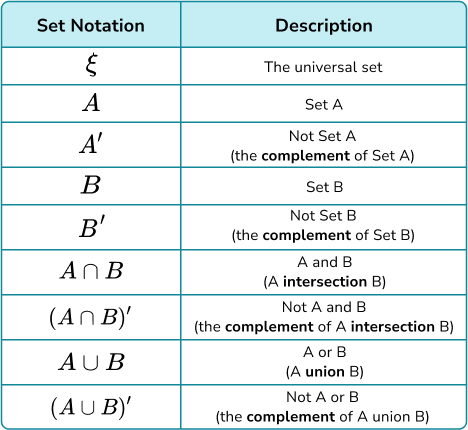
Step-by-step guide: Probability symbol
Probability notation
In maths we use some common probability notation in addition to standard mathematical notation and symbols. We use set notation as an efficient way of writing the probability of events happening or not happening. Events are notated using capital letters, as well as the use of some greek letters.
For example,
Probability, P(A) refers to the probability that an event, event A in this case, will occur.
Probability, P(B^{\prime}) refers to the probability that an event, event B in this case, will not occur.
Probability, P(A \cup B) refers to the probability of event A or event B happening or both.
Probability, P(A \cap B) refers to the probability of event A and B happening.
Step-by-step guide: Probability notation
How to describe probability in words
In order to describe probability in words:
- Consider whether the event you are trying to describe will definitely happen or not happen.
- Consider the likeliness of the event happening.
- Choose an appropriate word from the list to describe the probability.
Explain how to describe probability in words

Describing probability worksheet
Get your free describing probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONDescribing probability worksheet
Get your free describing probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONDescribing probability in words examples
Example 1: describing probability in words
Describe the likelihood that a newborn baby is a boy.
- Consider whether the event you are trying to describe will definitely happen or not happen.
A newborn baby being a boy could happen, so we cannot describe it as impossible.
A newborn baby can be a boy or a girl, so we cannot describe it as certain.
2Consider the likeliness of the event happening.
A newborn baby can be a boy or a girl. There are two possible options, both have a 50\% chance of happening.
3Choose an appropriate word from the list to describe the probability.
Two equally likely possible outcomes means we can say that there is an even chance that a newborn baby is a boy.
Example 2: describing probability in words
Describe the likelihood that a number less than 7 will be scored when an ordinary six-sided dice is rolled once.

Consider whether the event you are trying to describe will definitely happen or not happen.
An ordinary six-sided dice will have the numbers 1 to 6 on its faces. Scoring a 7 on an ordinary six-sided dice will definitely not happen.
Consider the likeliness of the event happening.
In this instance, we can ignore step 2. We do not need to consider the likelihood of this event further, it cannot happen.
Choose an appropriate word from the list to describe the probability.
Scoring a 7 on an ordinary six-sided dice cannot happen.
We can say that it is impossible to score a 7 on an ordinary six-sided dice.
Example 3: describing probability in words
In words, describe the probability that a red counter is obtained when a counter is taken at random from a bag that contains 11 red counters and 2 blue counters.
Consider whether the event you are trying to describe will definitely happen or not happen.
A red counter being obtained from the bag could happen, the bag does contain red counters, so we cannot describe it as impossible.
We could get a red or a blue counter out of the bag, so we cannot describe the probability of getting a red counter as certain.
Consider the likeliness of the event happening.
The chance of getting a red counter out of the bag is higher than blue. There are more red counters than blue in the bag. So we cannot describe it as unlikely, or even chance.
We can say that it is likely or very likely that we would obtain a red counter from the bag.
Choose an appropriate word from the list to describe the probability.
In this instance, the chance of getting a red counter from the bag is much higher than blue.
We can say that it is very likely we would obtain a red counter from the bag.
How to place events on a probability scale
In order to place events on a probability scale:
- Consider whether the event you are trying to describe will definitely happen or not happen.
- Consider the likeliness of the event happening.
- Choose the appropriate place on the scale to place the event.
Explain how to place events on a probability scale

Placing events on a probability scale examples
Example 4: placing events on a probability scale
Mark on the scale below, the probability that an ordinary six-sided dice is rolled and lands on an even number.
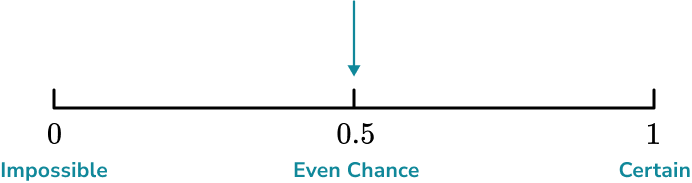
Consider whether the event you are trying to describe will definitely happen or not happen.
An ordinary six-sided dice will have the numbers 1 to 6 on its faces. Rolling an even number could happen, so we cannot describe it as impossible.
We could also roll an odd number on an ordinary six-sided dice, so we cannot describe it as certain.
Consider the likeliness of the event happening.
There are 3 odd numbers and 3 even numbers on an ordinary six-sided dice. Two possible outcomes, odd or even, both with a 50-50 chance.
Choose the appropriate place on the scale to place the event.
Two equally likely possible outcomes means we can say that there is an even chance that an even number is rolled, so we make a mark halfway between 0 (impossible) and 1 (certain), at 0.5 (even chance).
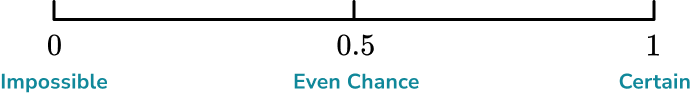
Example 5: placing events on a probability scale
There are 12 marbles in a bag.
5 marbles are yellow.
4 marbles are green.
2 marbles are red.

Lucas takes a marble at random from the bag.
On the probability scale, mark the probability that Lucas will take a red marble.
Consider whether the event you are trying to describe will definitely happen or not happen.
The bag does contain some red marbles. The chance of Lucas taking a red marble can happen, so we cannot describe it as impossible.
The bag does not only contain red marbles, it also has yellow and green marbles, so we cannot describe the chance of Lucas taking a red marble as certain.
Consider the likeliness of the event happening.
In the bag there are 12 marbles, 5 yellow, 4 green and 2 red. This means that there are 9 marbles that are not red, that Luca could get, and only 2 that are red.
The chance of Lucas picking out a red marble cannot be described as very likely, likely or even chance.
Choose the appropriate place on the scale to place the event.
It is not very likely that Lucas will pick a red marble out of the bag, so we need to place the event between 0 (impossible) and 0.5 (even chance).
In this instance, 2 out of 12 marbles are red, so we would place the event closer to 0 (impossible) than 0.5 (even chance).
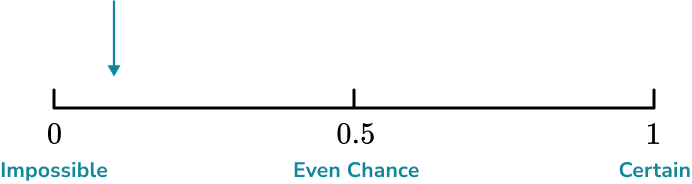
Example 6: placing events on a probability scale
Trevor uses some letter cards to spell the word “SEPTEMBER”.

Trevor takes one of these cards at random.
Mark on the scale below, the probability that Trevor takes a card with a letter A.
Consider whether the event you are trying to describe will definitely happen or not happen.
The word “SEPTEMBER” does not contain the letter A, so Trevor cannot pick a card that contains the letter A, it will definitely not happen.
Consider the likeliness of the event happening.
In this instance, we can ignore step 2. We do not need to consider the likelihood of this event further, it cannot happen.
Choose the appropriate place on the scale to place the event.
Picking a card containing the letter A, from the word “SEPTEMBER” cannot happen.
We can say that it is impossible for Trevor to pick a card containing the letter A.
Common misconceptions
- The probability scale goes from \bf{0} (impossible) to \bf{1} (certain)
Remember that impossible is at 0 and certain is at 1, when probability scales are marked numerically rather than with words.
For example,
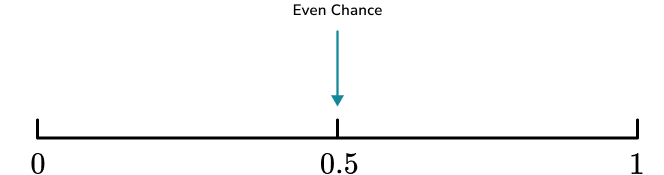
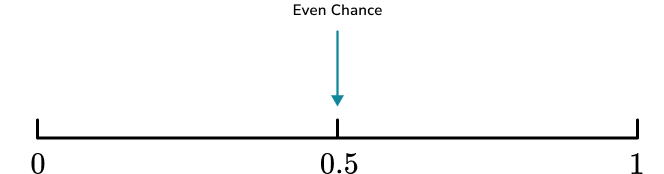
- Even Chance
An event can only be described as having an “even chance” of occurring if the number of times it could occur is exactly the same as the other possible outcome.
For example,
When flipping a coin, a coin only has two sides. One contains heads, and the other tails. So the coin landing on heads and the coin landing on tails has an equal chance of happening.
But just because an event has two outcomes, it does not mean that the two events have equal probabilities.
For example,
A cube has six faces. One face is red and the other 5 faces are blue. There are 2 outcomes, red and blue. But the probabilities are different.
The probability of getting red is \frac{1}{6} and the probability of getting blue is \frac{5}{6}.
Practice describing probability questions
1. Place the words in the box onto the probability scale.
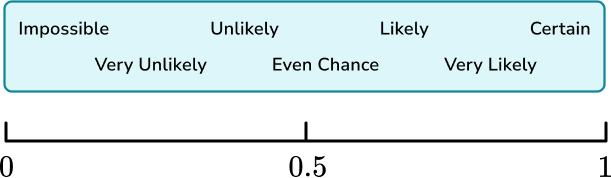

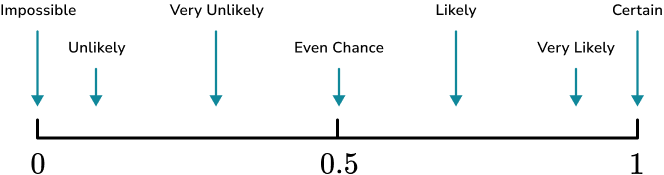

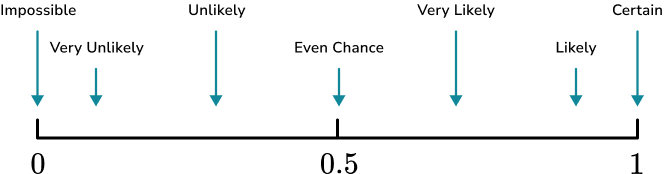

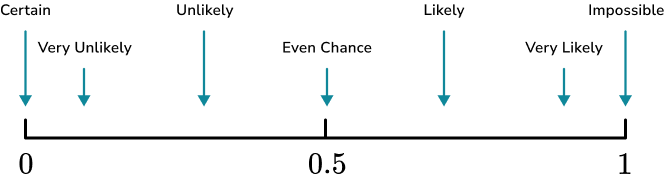

Remember that impossible is at 0 and certain is at 1, when probability scales are marked numerically rather than with words.
For example,
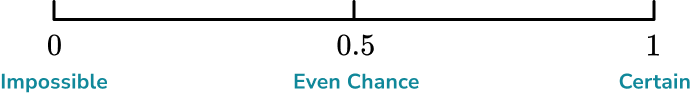
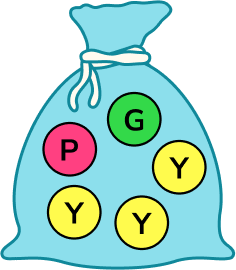
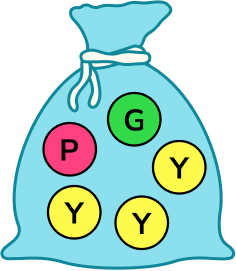
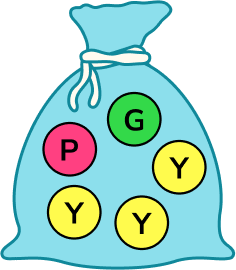
2. Use a word from the box to describe the probability that a yellow counter is picked from the bag below.

Impossible

Unlikely

Certain

Very likely

There are 3 yellow counters and 2 that are not yellow. There is more chance of picking a yellow counter.
3. Use a word from the box to describe the probability that a green counter is picked from the bag below.

Likely

Impossible

Very Unlikely

Certain

There is 1 green counter and 4 that are not green. There is more chance of picking a counter that is not green.
4. Use a word from the box to describe the probability that a red counter is picked from the bag below.

Unlikely

Impossible

Very Unlikely

Likely

There are no red counters in the bag, so a red counter cannot be picked.
5. Caitlin uses some letter cards to spell out the word “DECEMBER”.
![]()
Caitlin takes one of these cards at random.
Mark on the scale below, the probability that Caitlin takes a card containing the letter E.




There are 3 cards with the letter E and 5 cards that do not contain the letter E. There is more chance of picking a card that does not contain the letter E.
6. Caitlin uses some letter cards to spell out the word “DECEMBER”.
![]()
Caitlin takes one of these cards at random.
Mark on the scale below, the probability that Caitlin takes a card containing a consonant.
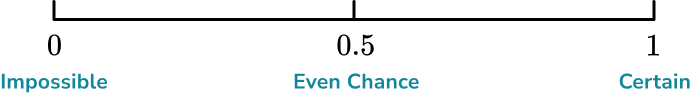




There are 5 cards that contain consonants and 3 cards that contain vowels. There is more chance of picking a card that contains a consonant.
Describing probability GCSE questions
1. 
Which word from the box best describes the likelihood of each of these events?
(a) A newborn baby is a girl.
(b) You throw an ordinary dice and it lands on a three.
(2 marks)
Even chance
(1)
Unlikely or very unlikely
(1)
2. A fair six-sided dice is thrown.

The probabilities of the following events have been marked on the probability scale below.
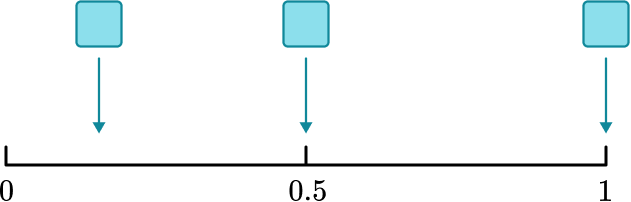
A: A number less than 7 is thrown.
B: A “5” is thrown.
C: An odd number is thrown.
Label each place marked on the scale with the appropriate letter.
(3 marks)
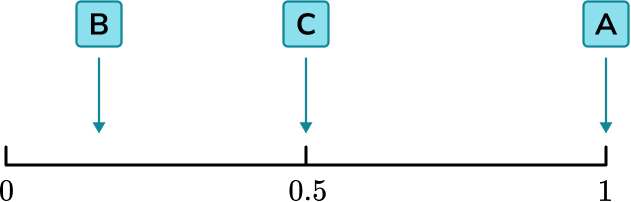
One mark per correct letter
(3)
3. Ashton spins a fair spinner with six sections.
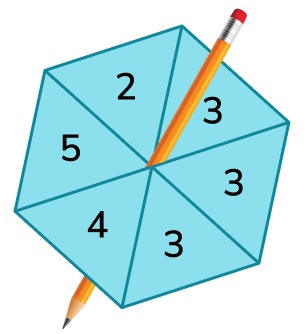

Use a word from the box which best describes the probability of each of the following events.
(a) The spinner will land on 3.
(b) The spinner will land on 6.
(c) The spinner will land on 5.
(d) The spinner will land on a number greater than 1.
(4 marks)
(a) Even chance
(1)
(b) Impossible
(1)
(c) Unlikely or very unlikely
(1)
(d) Certain
(1)
Learning checklist
You have now learned how to:
- Describe probability using words
- Place events on a probability scale
- Reason about the likelihood of an event happening
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.