One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Probability scale Mutually exclusive events Independent eventsThis topic is relevant for:

Combined Events Probability
Here we will learn about combined events in probability for both independent and dependent variables. We will also look at the use of sample space diagrams and Venn diagrams for combined probabilities.
There are also combined events worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are combined events in probability?
Combined events in probability are events that occur at the same time or in succession. We can calculate the likelihood of a certain combination of outcomes.
To do this we can use the \textbf{AND} probability rule. This rule states that the probability of outcome A occurring from one event \textbf{AND} outcome B occurring from a second event is the probability of outcome A multiplied by the probability of outcome B. If A and B are independent of each other.
P(A \textbf{ AND } B) = P(A) \ {\bf{\times}} \ P(B)What are combined events in probability?

What are combined events in probability?

Independent Combined Events
This rule can be readily applied to independent events. Events are independent if the occurrence of one event does not affect the occurrence of another.
To understand the \textbf{AND} probability rule, consider the following example.
A six-sided die is rolled and the suit of a card randomly chosen from a deck is noted.
We can enumerate the possible outcomes by creating a sample space diagram.
There are 24 different outcomes for these combined events.
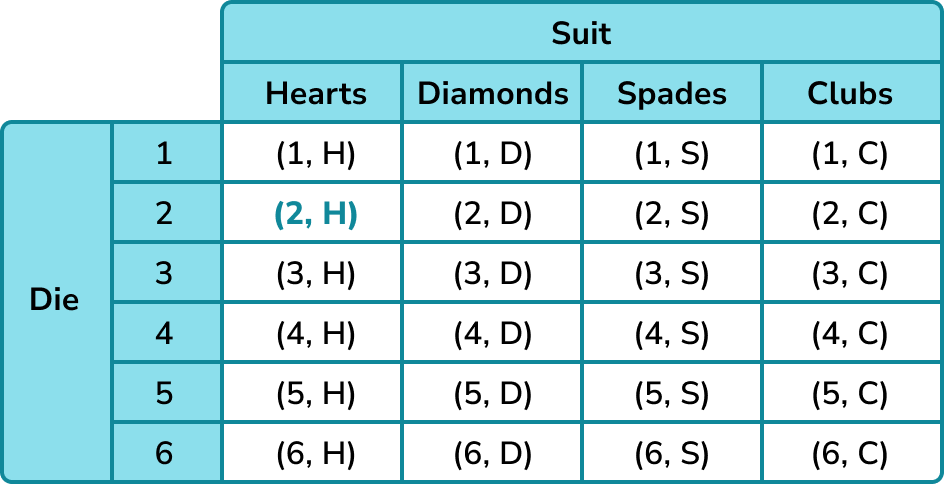
The probability of rolling a two and drawing a heart from the deck is \frac{1}{24} because this is one combination out of twenty-four possible combinations.
The \textbf{AND} probability rule can also be used as follows.
The probability of rolling a two on a six-sided die is \frac{1}{6}.
The probability of drawing a heart from a deck of cards is \frac{1}{4}.
The probability of rolling a two \textbf{AND} drawing a heart is therefore \frac{1}{6} \times \frac{1}{4}=\frac{1}{24}.

Sometimes a combination of both the \textbf{AND} and the \textbf{OR} probability rules are required in order to answer a question about combined events.
Tree diagrams can also be used to visualise combined events questions. The same rules will be used but a tree diagram can help make the probabilities needed for each question clearer.
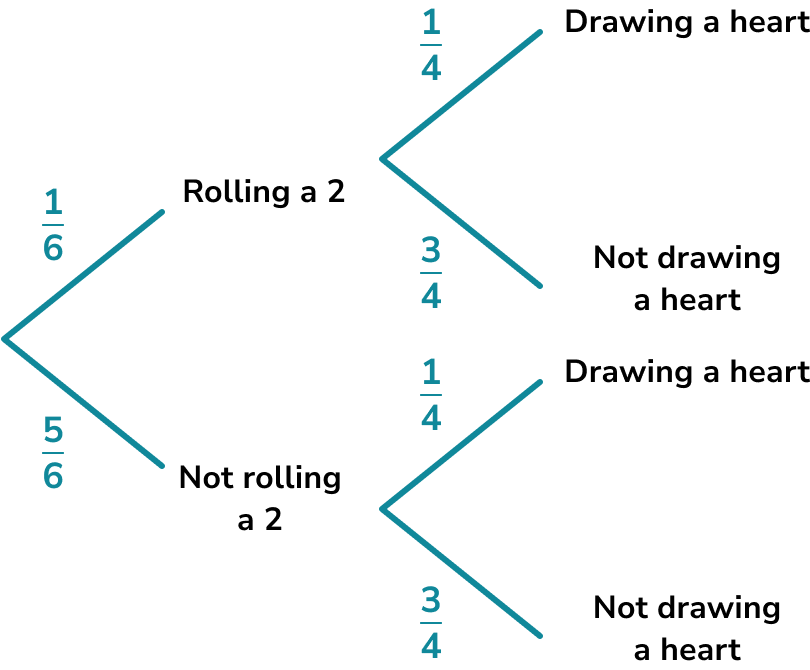
Step-by-step guide: Probability tree diagram
Enumeration
Enumeration is the act of counting or listing all possible items or combinations of items from a set or sets.
This can be done using a sample space diagram such as the table above or by using a method of systematic listing.
Step-by-step guide: Sample space diagram
Systematic Listing is a method to ensure a list of all outcomes from an event are listed in an organised way with none of the possibilities missed out.
Step-by-step guide: Systematic listing strategies
We could also find the number of total outcomes using the product rule for counting.
The product rule for counting is a method for finding the total number of combinations of selecting items from a set or sets.
Step-by-step guide: Product rule for counting
Dependent combined events
The rule can be adapted and applied to dependent events. Events are dependent if the occurrence of one event affects the occurrence of another.
For example, the probability of a bus being late could depend on whether it is raining that day. The probability of it raining is 0.4. If it rains the probability of the bus being late is 0.7, if it is not raining the probability of the bus being late is 0.2.
The events could be listed as,
Not raining, Bus is on time
Raining, Bus is on time
Not raining, Bus is late
Raining, Bus is late.
This could also be displayed using a tree diagram.
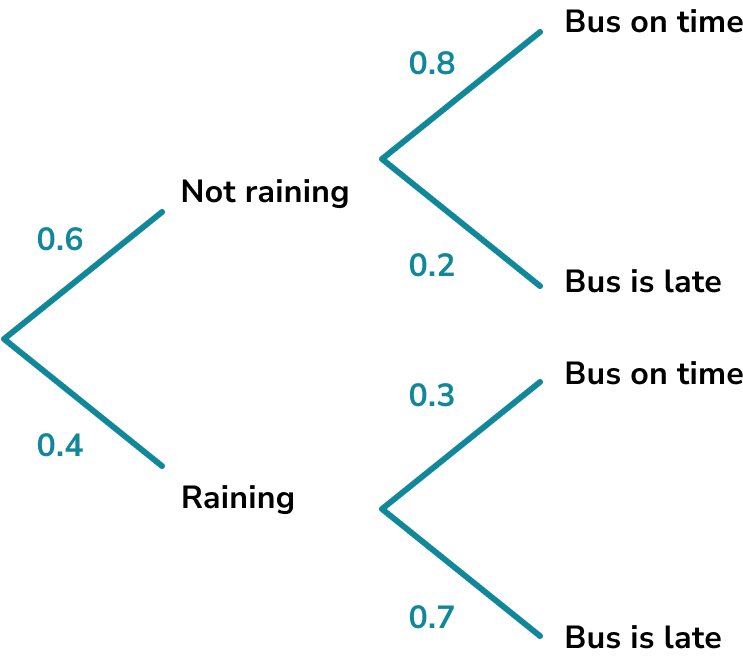
The probability of the bus being late would be
0.6\times 0.2+0.4\times 0.7=0.12+0.28=0.4 .
How to calculate the probability of combined events
In order to calculate the probability of combined events:
- Identify the separate events* in the question and the probabilities of the required outcomes.
- Write a sentence combining the required outcomes of the events using the word \textbf{AND} .
- Apply the \textbf{AND} probability rule by multiplying together the probabilities of the required outcomes.
*The phrase ‘separate events’ is referencing a number of important factors which must be considered when answering a question about combined probabilities. The easiest way to learn these factors is through examples but below is a list to refer to.
(a) The outcomes of an individual event should be mutually exclusive.
(b) If events are independent then the \text{AND} probability rule can be instantly applied.
(c) If events are dependent then in some cases the \text{AND} probability rule cannot be applied, while in other cases conditional probabilities can be calculated and then the \text{AND} probability rule can be applied.
(d) Sometimes events and outcomes can be confused. If there is only one event, but the outcomes are combined then a two-way table or Venn Diagram is the best way to solve the problem. The \text{AND} probability rule cannot be applied to a single event.
(e) Tree diagrams are often used to help illustrate the separate events and possible outcomes.
Explain how to calculate the probability of combined events


Combined events probability worksheet

Get your free combined events probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Combined events probability worksheet

Get your free combined events probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREECombined events probability examples
Example 1: applying the AND probability rule to independent events

This pentagonal spinner has 5 sections. 3 sections are red and 2 sections are blue. The spinner is spun twice.
Calculate the probability that the spinner lands on red both times.
- Identify the separate events in the question and the probabilities of the individual outcomes.
The probability of the spinner landing on red is \frac{3}{5}.
2Write a sentence combining the required outcomes of the events using the word \textbf{AND} .
The probability of the spinner landing on red \textbf{AND} then red.
3Apply the \textbf{AND} probability rule by multiplying together the probabilities of the required outcomes.
\frac{3}{5} \times \frac{3}{5}=\frac{9}{25}Example 2: applying both the AND and the OR probability rules to independent events

This pentagonal spinner has 5 sections. 3 sections are red, and 2 sections are blue. The spinner is spun twice.
Calculate the probability that the spinner lands on a different colour each time.
Identify the separate events in the question and the probabilities of the individual outcomes.
The probability of the spinner landing on red is \frac{3}{5}.
The probability of the spinner landing on blue is \frac{2}{5}.
Write a sentence combining the required outcomes of the events using the word \textbf{AND} .
Note here that there are two ways of the spinner landing on a different colour each time and the OR probability rule also needs to be applied.
The probability of the spinner landing on red \textbf{AND} then blue.
\textbf{OR}
The probability of the spinner landing on blue \textbf{AND} then red.
Apply the \textbf{AND} probability rule by multiplying together the probabilities of the required outcomes.
Example 3: combined events and sample space diagrams
Charlotte has two red balls and one green ball. Joe has one red ball, one green ball and one yellow ball. Charlotte and Joe choose one ball each from their own collections.
(a) Draw a sample space diagram to represent all the outcomes of Charlotte and Joe’s selections.
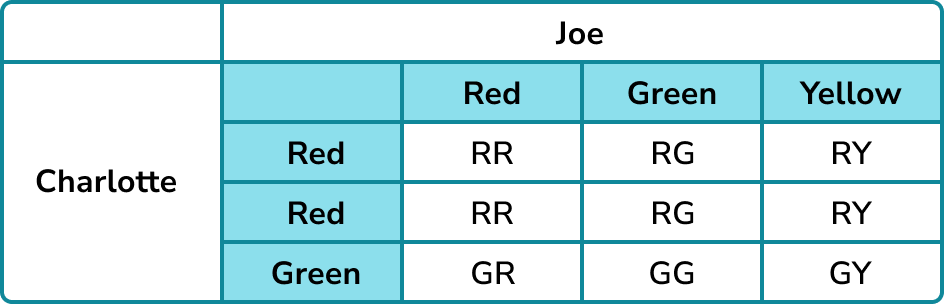
(b) What is the probability Charlotte chooses green and Joe chooses red?
Option 1: using the table.
There are 9 combined outcomes for these events. One of these combinations is Charlotte choosing green and Joe choosing red. Hence the combined probability is one out of nine.
\frac{1}{9}
Option 2: using the \text{AND} probability rule.
Probability of Charlotte choosing green =\frac{1}{3}.
Probability of Joe choosing red =\frac{1}{3}.
Combined probability =\frac{1}{3} \times \frac{1}{3}=\frac{1}{9}.
(c) What is the probability that Charlotte chooses red and Joe chooses yellow?
Option 1: using the table.
There are 9 combined outcomes for these events. There are two combinations where Charlotte chooses red and Joe chooses yellow. Hence the combined probability is two out of nine.
\frac{2}{9}
Option 2: using the \text{AND} probability rule.
Probability of Charlotte choosing red =\frac{2}{3}.
Probability of Joe choosing yellow = \frac{1}{3}.
Combined probability =\frac{2}{3} \times \frac{1}{3}=\frac{2}{9}.
(d) What is the probability that they both choose the same colour?
Option 1: using the table.
There are 9 combined outcomes for these events. There are three combinations where Charlotte and Joe choose the same colour (RR, RR and GG). Hence the combined probability is three out of nine.
\frac{3}{9}=\frac{1}{3}
Option 2: using the \text{AND} and the \text{OR} probability rules.
Probability of Charlotte choosing red \text{AND} Joe choosing red =\frac{2}{3} \times \frac{1}{3}=\frac{2}{9}.
Probability of Charlotte choosing green \text{AND} Joe choosing green = \frac{1}{3} \times \frac{1}{3}=\frac{1}{9}.
Probability of both choosing red OR both choosing green =\frac{2}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}.
(e) What is the probability they both choose a different colour?
Option 1: using the table.
There are 9 combined outcomes for these events. There are six combinations where Charlotte and Joe choose a different colour (RG, RG, RY, RY, GR, GY). Hence the answer is six out of nine.
\frac{6}{9}=\frac{2}{3}
Option 2: using probabilities summing to one.
From part (d), the probability that they both choose the same colour is \frac{1}{3}.
Using the property that the probabilities of an exhaustive set of mutually exclusive events sum to one, the answer can be found by subtracting the probability that they choose the same colour from 1.
1-\frac{1}{3}=\frac{2}{3}.
Note: As shown, all answers to example 3 can be calculated using the \text{AND} probability rule. However, if you have drawn a sample space diagram it is often quicker to use the information from the table.
Example 4: combined events and permutations
Abdul tosses 3 fair coins. What is the probability that he will get exactly one head?
Identify the separate events in the question and the probabilities of the individual outcomes.
There are three events – the toss of each fair coin. The outcome of each event can be heads or tails.
Probability of heads = 0.5.
Probability of tails = 0.5.
Write a sentence combining the required outcomes of the events using the word \textbf{AND} .
The probability of getting a head \textbf{AND} a tail \textbf{AND} a tail.
Note here that there are different permutations of the required outcome of ‘exactly one head’. These are,
\begin{aligned} &HTT \\ &THT \\ &TTH \end{aligned}
We want the probability of getting
head \textbf{AND} tail \textbf{AND} tail
\textbf{OR}tail \textbf{AND} head \textbf{AND} tail
\textbf{OR}tail \textbf{AND} tail \textbf{AND} head.
Apply the \textbf{AND} probability rule by multiplying together the probabilities of the required outcomes.
This is the probability of a single combined outcome which shows 1 head and 2 tails.
0.125 + 0.125 + 0.125 = 0.375
The probability must be multiplied by 3 because there are 3 different ways of getting 1 head and 2 tails and each way has the same probability of occurring.
Example 5: dependent events
There are 7 sweets in a bowl. 5 sweets are strawberry, and 2 sweets are lemon. Without looking Anouksha takes a sweet from the bowl and then Henri takes one.
Calculate the probability of the following.
(a) Anouksha takes a strawberry sweet and Henri takes a lemon sweet.
Identify the separate events in the question and the probabilities of the individual outcomes.
The probability Anouksha takes a strawberry sweet is \frac{5}{7}.
The probability that Henri takes a lemon sweet is \frac{2}{6}.
(These events are dependent. As Anouksha has already taken a sweet, there are only 6 left, and 2 of those are lemon.)
Write a sentence combining the required outcomes of the events using the word \textbf{AND} .
The probability of Anouksha taking a strawberry sweet \text{AND} Henri taking a lemon sweet.
Apply the \textbf{AND} probability rule by multiplying together the probabilities of the required outcomes.
(b) Anouksha and Henri both take the same flavour.
Identify the separate events in the question and the probabilities of the individual outcomes.
There are two possibilities here, they both take a strawberry sweet or they both take a lemon sweet.
Strawberry \text{AND} strawberry:
The probability Anouksha takes a strawberry sweet is \frac{5}{7}.
The probability that Henri also takes a strawberry sweet is \frac{4}{6}.
(These events are dependent. As Anouksha has already taken a strawberry sweet, there are only 6 sweets left, and 4 of those are strawberry.)
Lemon \text{AND} lemon:
The probability Anouksha takes a lemon sweet is \frac{2}{7}.
The probability that Henri also takes a lemon sweet is \frac{1}{6}.
(These events are dependent. As Anouksha has already taken a lemon sweet there are only 6 sweets left now, and 1 of those is lemon.)
Write a sentence combining the required outcomes of the events using the word \textbf{AND} .
The probability of Anouksha taking a strawberry sweet \textbf{AND} Henri taking a strawberry sweet.
\textbf{OR}
The probability of Anouksha taking a lemon sweet \textbf{AND} Henri taking a lemon sweet.
Apply the \textbf{AND} probability rule by multiplying together the probabilities of the required outcomes.
Common misconceptions
- Permutations
It is a common error for students to calculate a combined probability but forget about the different permutations.
Look carefully at example 5. Three coins are tossed, and the outcome of one head and two tails is 0.5 \times 0.5 \times 0.5 = 0.125. However, there are 3 different permutations for one head and two tails (HTT, THT, TTH). Therefore, this probability needs multiplying by
3.
0.125 \times 3 = 0.375.
- Confusing events with outcomes
When answering a probability question, think carefully about how many events the question is referring to. In order to apply the \text{AND} probability rule there needs to be more than one event.
If there is only a single event and you are combining outcomes instead, you should use a two-way table or Venn diagram to help you answer the question.
- Dependent events
When answering a question about combined events, always think carefully about whether the events are independent or dependent. For dependent events the probability of the second event will change depending on the outcome of the first event.
It is a common error for students not to realise events are dependent and miscalculate the probability of the second event.
Practice combined events probability questions
1. If the occurrence of one event does not affect the occurrence of another, what are these events?
Dependent

Independent

Mutually exclusive

Disjoint

Events are described as independent if they are not affected by each other.
2. There are 3 blue counters and 1 yellow counter. A counter is chosen at random, its colour is recorded, and then it is replaced. A second counter is then chosen, and its colour is recorded.
What is the probability that both counters are blue?




The probability of getting a blue counter is \frac{3}{4}.
The probability of getting a blue counter \text{AND} a blue counter is
\frac{3}{4} \times \frac{3}{4}=\frac{9}{16}.
3. Two dice are rolled. What is the probability of rolling the combination of a 1 and a 6?




The probability of getting a one \text{AND} a six is
\frac{1}{6} \times \frac{1}{6}=\frac{1}{36}.
The probability of getting a six \text{AND} a one is
\frac{1}{6} \times \frac{1}{6}=\frac{1}{36}.
It could be the first combination \text{OR} the second combination so
\frac{1}{36}+\frac{1}{36}=\frac{2}{36}=\frac{1}{18}.
4. The sample space diagram shows the possible outcomes for the combined events of rolling of a six-sided die and noting the suit of a card drawn from a standard deck.
What is the probability that the outcome is an even number and a spade?
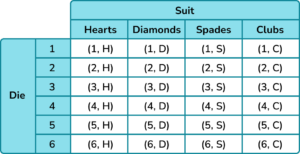




The sample space diagram shows 24 possible outcomes. Three of these outcomes are even numbers with a spade (2,S) \ (4,S) \ (6,S). The probability is therefore
\frac{3}{24}=\frac{1}{8}.
Alternatively you can use the \text{AND} probability rule. The probability of an even number on a six-sided die is
\frac{3}{6}=\frac{1}{2}.
The probability of a spade is \frac{1}{4}.
The probability of an even number \text{AND} a spade is
\frac{1}{2} \times \frac{1}{4}=\frac{1}{8}.
5. Three coins are tossed. What is the probability that the outcome will have at least two heads?




In total there are 8 outcomes. There are 4 outcomes with at least two heads.
The probability is \frac{4}{8}=\frac{1}{2}.
The correct answer as a decimal is 0.5.
Alternatively, you can use the \text{AND} probability rule.
The probability of any combined outcome when three coins are tossed is
0.5 \times 0.5 \times 0.5 = 0.125.
There are 4 combinations which have at least two heads.
Therefore 0.125 \times 4 = 0.5.
6. A bowl has two bananas and four apples in it. Harry picks a piece of fruit at random and then Zain picks a piece of fruit at random.
What is the probability that both Harry and Zain pick an apple?




The probability that Harry picks an apple is \frac{4}{6}.
The probability that Zain picks an apple given that Harry has picked an apple is \frac{3}{5}.
The probability that Harry picks an apple \text{AND} then Zain picks an apple is
\frac{4}{6} \times \frac{3}{5}=\frac{12}{30}=\frac{2}{5}.
Combined events probability GCSE questions
1. A weather forecast says,
The probability that it will rain on Saturday is 0.7.
The probability that it will rain on Sunday is 0.5.
(a) Calculate the probability it will rain on Saturday and Sunday.
(b) Calculate the probability it will rain on just one of the days.
(3 marks)
(a)
Probability that it will rain on Saturday \text{AND} rain on Sunday = 0.7 \times 0.5 = 0.35 .
(1)
(b)
Probability that it will not rain on Saturday = 1 – \ 0.7 = 0.3.
Probability that it will not rain on Sunday = 1 – \ 0.5 = 0.5.
Probability that it will rain on Saturday \text{AND} not rain on Sunday = 0.7 \times 0.5 = 0.35 .
Probability that it will not rain on Saturday \text{AND} rain on Sunday = 0.3 \times 0.5 = 0.15 .
(1)
Probability that it will rain only on Saturday \text{OR} rain only on Sunday = 0.35 \times 0.15 = 0.5 .
(1)
2.
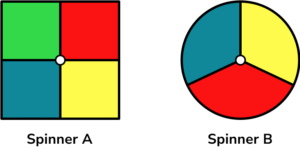
Spinner A and Spinner B are both spun once.
(a) Draw a sample space diagram to show all the possible outcomes.
(b) What is the probability of spinner A landing on red and spinner B landing on blue?
(c) What is the probability that both spinners land on the same colour?
(d) What is the probability that at least one of the spinners lands on yellow?
(5 marks)
(a)
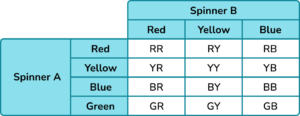
A table drawn with the separate outcomes listed for spinner A and spinner B and an attempt to complete the combined outcomes.
(1)
Table complete and all combined outcomes listed.
(1)
(b) \frac{1}{12}
(1)
(c) \frac{3}{12}=\frac{1}{4}
(1)
(d) \frac{6}{12}=\frac{1}{2}
(1)
3. There are 5 yellow balls and 3 red balls in a bag. Tamanga picks a ball from the bag at random with his left hand. He then does the same with his right hand.
(a) What is the probability that Tamanga has a red ball in each hand?
(b) What is the probability that Tamanga has one yellow ball and one red ball in his hands?
(5 marks)
(a)
Identify the probability of his left hand picking a red ball as \frac{3}{8} and his right hand picking a red ball as \frac{2}{7} .
(1)
\frac{3}{8} \times \frac{2}{7}=\frac{6}{56}=\frac{3}{28}(1)
(b)
Probability of picking a yellow \text{AND} then red \frac{5}{8} \times \frac{3}{7}=\frac{15}{56}.
Probability of picking a red \text{AND} then yellow \frac{3}{8} \times \frac{5}{7}=\frac{15}{56} .
(1)
Probability of yellow&red \text{OR} red&yellow \frac{15}{56}+\frac{15}{56}=\frac{30}{56}=\frac{15}{28}.
(1)
Learning checklist
You have now learned how to:
- Calculate the probability of independent and dependent combined events and know the underlying assumptions
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.