One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
This topic is relevant for:

Numerator And Denominator
Here we will learn about the numerator and denominator of fractions, including equivalent fractions, improper fractions, unit fractions and mixed numbers.
There are also equivalent fraction worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is numerator and denominator?
The numerator and denominator of a fraction are the top number and bottom number parts of a fraction.
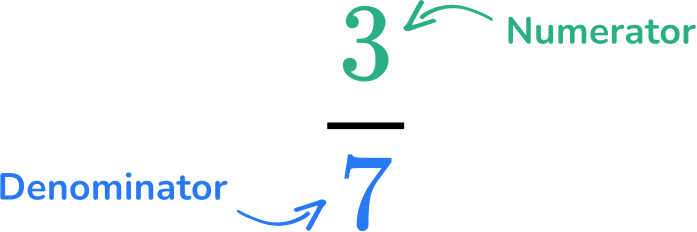
- A fraction visually displays a division.
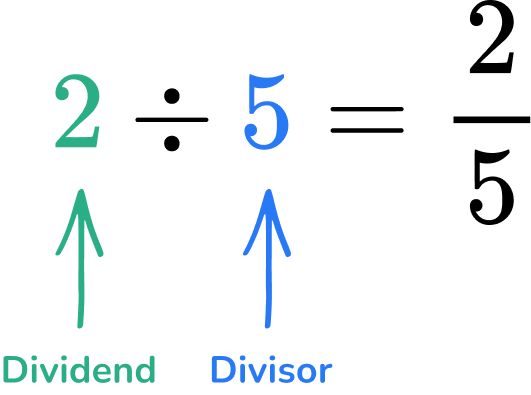
The numerator represents the dividend and the denominator represents the divisor.
- A proper fraction is one which is part of a whole (less than 1 ), where the numerator is less than the denominator.
For example,
\cfrac{2}{7} \, , \, \cfrac{3}{5} \, , \, \cfrac{4}{11} are all proper fractions.
- A fraction can be simplified if the numerator and denominator have a common factor.
For example,
\cfrac{6}{8} is not in its simplest form. 6 and 8 have a common factor of 2.
Dividing both the numerator and denominator by their highest common factor (HCF) will produce an equivalent fraction in its simplest form.
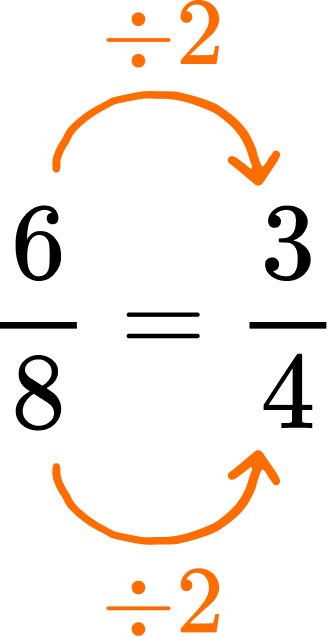
\cfrac{6}{8} is equivalent to \cfrac{3}{4}.
- A unit fraction is a type of fraction with a numerator of 1.
For example,
\cfrac{1}{2} \, , \, \cfrac{1}{3} \, , \, \cfrac{1}{9} are all unit fractions.
- If the numerator of a fraction is greater than the denominator of the fraction, the fraction is called an improper fraction.
For example,
\cfrac{7}{3} is an improper fraction because 7>3.
Improper fractions can be converted to mixed numbers.
- A mixed number (also called mixed fraction) has an integer part and a fractional part.
We can convert an improper fraction to a mixed number by dividing the numerator by the denominator to find the integer and the remainder. We can then write the remainder on top of the original denominator as the fractional part, next to the integer part.
For example,
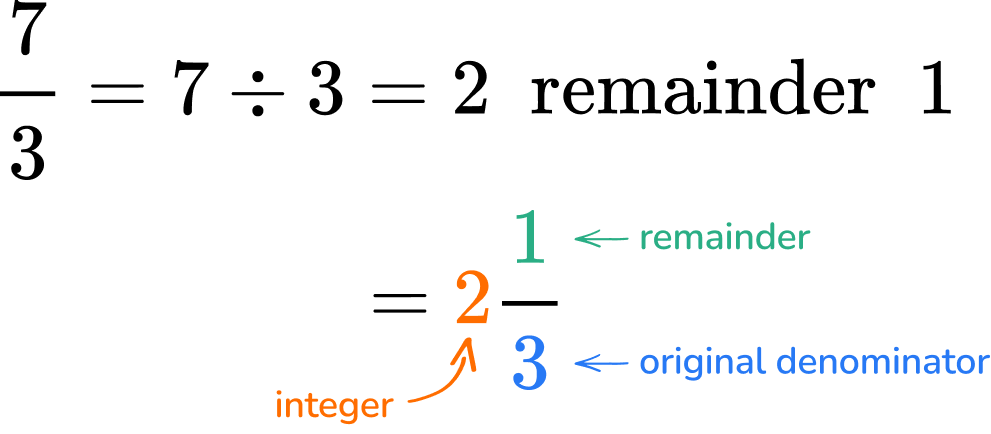
If the numerator is a multiple of the denominator, the fraction will be equivalent to an integer. We can just carry out the division to find the integer value.
For example,
\cfrac{12}{3}=12\div3=4
If the numerator is equal to the denominator, the fraction will be equivalent to 1.
For example,
\cfrac{13}{13}=13\div 13=1
- If we perform a short division process we can also convert a fraction to a decimal.
If we wanted to convert three eighths into a decimal, we can use the “bus stop” division to find the equivalent decimal.
For example,
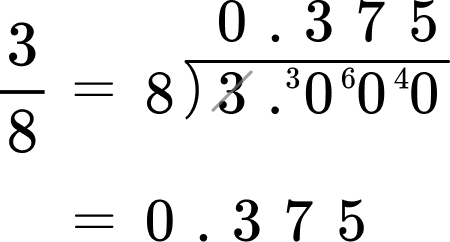
- If a fraction has a denominator which is 100, it can easily be converted to a percentage.
For example,
\cfrac{37}{100}=37\%
\cfrac{14}{25}=\cfrac{14\times 4}{25\times 4}=\cfrac{56}{100}=56\%
- There are times we will need to compare, add or subtract fractions.
To do this we need a common denominator.
For example,
\cfrac{3}{7} and \cfrac{1}{2} do not have common denominators.
We can find the lowest common multiple (LCM) of the denominators to then convert both fractions to equivalent fractions with a common denominator.
7 and 2 have a lowest common multiple of 14.
Converting both fractions gives us
\cfrac{3}{7}=\cfrac{3\times 2}{7\times 2}=\cfrac{6}{14}
\cfrac{1}{2}=\cfrac{1\times 7}{2\times 7}=\cfrac{7}{14}
Now we have a common denominator, we can compare, add or subtract the two fractions.
Comparing,
\cfrac{6}{14}<\cfrac{7}{14} so \cfrac{3}{7}<\cfrac{1}{2}.
Adding,
\cfrac{3}{7}+\cfrac{1}{2}=\cfrac{6}{14}+\cfrac{7}{14}=\cfrac{13}{14}.
Finding common denominators is also an alternative way to divide fractions.
\cfrac{3}{7}\div \cfrac{1}{2}=\cfrac{6}{14}\div\cfrac{7}{14}=\cfrac{6\div 7}{14\div 14}=\cfrac {6\div 7}{1}=\cfrac{6}{7}
What is numerator and denominator?

How to use numerators and denominators
In order to use numerators and denominators:
- Identify the numerator and denominator.
- Compare.
a) Do they have a common factor?
b) Is the numerator greater than the denominator?
c) Is the numerator a multiple of the denominator? - If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
Explain how to use numerators and denominators


Equivalent fractions worksheet (includes numerator and denominator)

Get your free numerator and denominator worksheet of 20+ equivalent fractions questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Equivalent fractions worksheet (includes numerator and denominator)

Get your free numerator and denominator worksheet of 20+ equivalent fractions questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on fractions
Numerator and denominator is part of our series of lessons to support revision on fractions. You may find it helpful to start with the main fractions lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Numerator and denominator examples
Example 1: simplifying a proper fraction
Simplify \cfrac{12}{18}.
- Identify the numerator and denominator.
The numerator is 12 and the denominator is 18.
2Compare.
a) Do they have a common factor?
Yes, the highest common factor of 12 and 18 is 6.
b) Is the numerator greater than the denominator?
No.
c) Is the numerator a multiple of the denominator?
No.
3If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
Dividing both 12 and 18 by 6 gives \cfrac{12}{18}=\cfrac{2}{3}.
Example 2: converting an improper fraction to a mixed number
Write \cfrac{11}{3} as a mixed number.
Identify the numerator and denominator.
The numerator is 11 and the denominator is 3.
Compare.
a) Do they have a common factor?
No.
b) Is the numerator greater than the denominator?
Yes, 11 is greater than 3.
c) Is the numerator a multiple of the denominator?
No.
If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
Dividing 11 by 3 gives 3 remainder 2. This means that \cfrac{11}{3} \, is the same as 3 whole ones plus 2 thirds.
\cfrac{11}{3} =3\cfrac{2}{3}Example 3: converting an improper fraction to an integer
Write \cfrac{24}{6} as an integer.
Identify the numerator and denominator.
The numerator is 24 and the denominator is 6.
Compare.
a) Do they have a common factor?
Yes. 6 goes into both 24 and 6.
b) Is the numerator greater than the denominator?
Yes, 24 is greater than 6.
c) Is the numerator a multiple of the denominator?
Yes, 24 is a multiple of 6.
If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
Dividing 24 by 6 gives 4.
\cfrac{24}{6}=4
Example 4: converting an improper fraction to a mixed number and simplifying
Write \cfrac{25}{15} as a mixed number in its simplest form.
Identify the numerator and denominator.
The numerator is 25 and the denominator is 15.
Compare.
a) Do they have a common factor?
Yes, 5 is a common factor of both 25 and 15.
b) Is the numerator greater than the denominator?
Yes, 25 is greater than 15.
c) Is the numerator a multiple of the denominator?
No.
If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
Dividing both 25 and 15 by 5 gives \cfrac{5}{3}. This can now be converted to a mixed number.
\cfrac{25}{15}=\cfrac{5}{3}=1\cfrac{2}{3}
Example 5: converting a fraction to a decimal
Write \cfrac{3}{8} as a decimal.
Identify the numerator and denominator.
The numerator is 3 and the denominator is 8.
Compare.
a) Do they have a common factor?
No.
b) Is the numerator greater than the denominator?
No, 3 is not greater than 8.
c) Is the numerator a multiple of the denominator?
No.
If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
This question requires the numerator to be divided by the denominator to get a decimal.
\cfrac{3}{8}=3\div 8=0.375
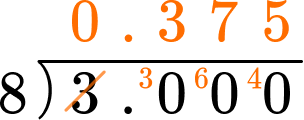
Example 6: converting a fraction to a percentage
Write \cfrac{13}{20} as a percentage.
Identify the numerator and denominator.
The numerator is 13 and the denominator is 20.
Compare.
a) Do they have a common factor?
No.
b) Is the numerator greater than the denominator?
No.
c) Is the numerator a multiple of the denominator?
No.
If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
The question requires the fraction to be written as a percentage. There are several ways to do this. One method is to convert the fraction so its denominator is 100.
Since 20 is a factor of 100, this can be done by multiplying the numerator and the denominator by 5.
\cfrac{13}{20}=\cfrac{13\times 5}{20\times 5}=\cfrac{65}{100}=65\%
Alternatively we could multiply the original fraction by 100.
\cfrac{13}{20}\times 100=\cfrac{1300}{20}=65\%
Or convert the original fraction to a decimal and then multiply by 100.
\cfrac{13}{20}\times 100=0.65\times 100=65\%
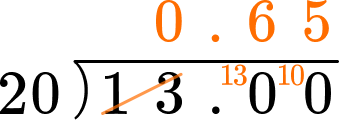
Example 7: converting a mixed number to an improper fraction
Write 7 \cfrac{1}{4} as an improper fraction.
Identify the numerator and denominator.
The numerator of the fraction is 1 and the denominator is 4.
Compare.
a) Do they have a common factor?
No.
b) Is the numerator greater than the denominator?
No.
c) Is the numerator a multiple of the denominator?
No.
If (a) simplify the fraction. If (b) convert to a mixed number. If (c) divide to get an integer.
The question requires the mixed number to be written as a fraction. This is done by multiplying the integer part by the denominator and adding it to the numerator.
This becomes the numerator of the improper fraction. The denominator stays the same.
7\cfrac{1}{4}=\cfrac{7\times 4+1}{4}=\cfrac{29}{4}
Common misconceptions
- Not using common numerators to compare fractions
Fractions can be compared with common numerators, not just common denominators, \cfrac{6}{11}>\cfrac{6}{17}.
If two fractions have the same numerator, the one with the smaller denominator will be the larger fraction.
- Not simplifying the fraction when converting a mixed number
When converting \cfrac{24}{16} to a mixed number it is important to also simplify the fraction.
\cfrac{24}{16}=1\cfrac{8}{16}=1\cfrac{1}{2}
- Not simplifying a fraction fully
We must be careful to divide both the numerator and the denominator by their highest common factor to simplify a fraction fully. This can be done in stages if necessary.
\cfrac{60}{96}=\cfrac{30}{48}=\cfrac{15}{24}=\cfrac{5}{8}
Practice numerator and denominator questions
1. Simplify \cfrac{60}{135} fully.




The HCF of 60 and 135 is 15. Divide both by 15 to get the simplified fraction.
\cfrac{60}{135}=\cfrac{60\div 15}{135\div 15}=\cfrac{4}{9}
2. Complete the missing numerator.
\cfrac{7}{8}=\cfrac{}{40}




The denominator has been multiplied by 5 so we need to multiply 7 by 5.
\cfrac{7}{8}=\cfrac{7\times 5}{8\times 5}=\cfrac{35}{40}
3. Complete the missing denominator.
\cfrac{18}{22}=\cfrac{45}{}




The numerator has been multiplied by 2.5 so we need to multiply 22 by 2.5.
45\div 18=2.5
\cfrac{18}{22}=\cfrac{18\times 2.5}{22\times 2.5}=\cfrac{45}{55}
4. Convert \cfrac{17}{7} to a mixed number.




7 goes into 17 twice, remainder 3.
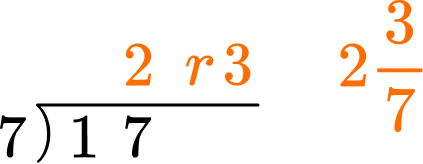
\cfrac{17}{7}=\cfrac{2\times 7+3}{7}=2\cfrac{3}{7}
5. Simplify \cfrac{64}{16} fully.




64 is a multiple of 16 so just perform the division.
\cfrac{64}{16}=64\div 16=4
OR cancel in steps
\cfrac{64}{16}=\cfrac{32}{8}=\cfrac{16}{4}=\cfrac{8}{2}=4
6. Write \cfrac{7}{12} and \cfrac{4}{15} with lowest common denominators.
\cfrac{28}{48} \, and \, \cfrac{28}{105}

\cfrac{28}{60} \, and \, \cfrac{20}{60}

\cfrac{35}{60} \, and \, \cfrac{16}{60}

\cfrac{7}{60} \, and \, \cfrac{4}{60}

The LCM of 12 and 15 is 60. Multiply 7 by 5 and 4 by 4 to give the correct numerators.
\cfrac{7}{12}=\cfrac{7\times 5}{12\times 5}=\cfrac{35}{60}
\cfrac{4}{15}=\cfrac{4\times 4}{15\times 4}=\cfrac{16}{60}
Numerator and denominator GCSE questions
1. Which is larger \cfrac{17}{24} or \cfrac{11}{15} ?
Give a reason for your answer.
(2 marks)
\cfrac{17}{24}=\cfrac{85}{120} \, or \, \cfrac{11}{15}=\cfrac{88}{120}
(1)
\cfrac{11}{15}
(1)
2. Write 4\cfrac{5}{13} as an improper fraction in its simplest form.
(2 marks)
4\times 13+5=57
Numerator is 57.
(1)
\cfrac{57}{13}
(1)
3. Simplify the algebraic fraction, \cfrac{12xyz}{18x^{2}z}.
(2 marks)
\cfrac{2}{3}
(1)
\cfrac{2y}{3x}
(1)
Learning checklist
You have now learned how to:
- Simplify fractions
- Find equivalent fractions
- Convert between improper fractions and mixed numbers
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.