GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

Area of a rectangle Area of a quadrilateral Area of a triangle Area of an isosceles triangle Area of compound shapes Interior angles of a polygons Angles in a triangle Pythagoras theorem Trigonometry

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes Area

Area of A Pentagon

Area Of A Pentagon

Here we will learn about the area of a pentagon, including how to find the area of a pentagon made from a triangle and a rectangle and how to find the area of a regular pentagon.

There are also area of a pentagon worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the area of a pentagon?

The area of a pentagon is the amount of space inside a five-sided polygon.

What is the area of a pentagon?

● Area of an irregular pentagon

An irregular pentagon may have been formed by combining other shapes such as rectangles and triangles. The area of each of these can be found and added together to find the area of the pentagon.

For example,

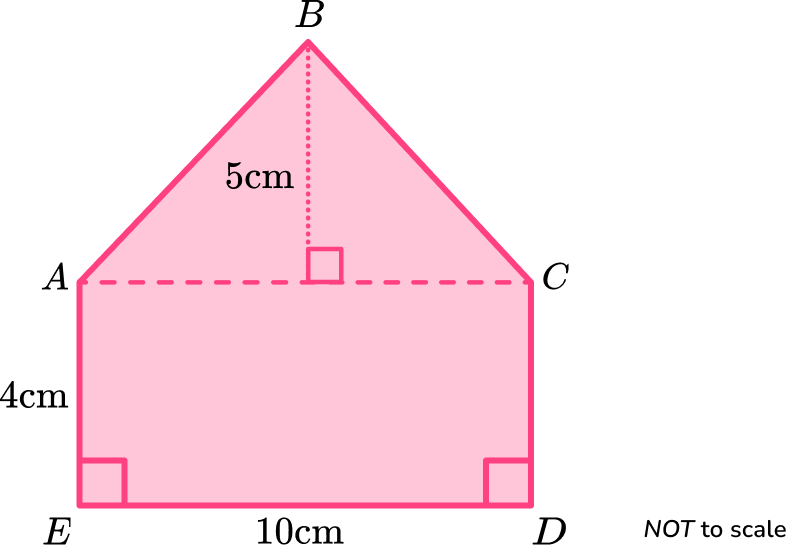
The area of irregular pentagon $\text{ABCDE}$ is

\text{Total area}=(\frac{1}{2}\times 10\times 5)+(4\times 10)=25+40=65 \ cm^2.

● Area of a regular pentagon

A regular pentagon has $5$ equal sides and all the interior angles are also equal.

The area of a regular polygon can be found by splitting the shape into congruent isosceles triangles. We can find the area of one of the triangles and then multiply by the number of sides to find the total area of the regular polygon.

The area of a regular pentagon can be simplified to

\text{Area of regular pentagon}=5\times \text{area of one triangle}.

The area of a triangle can be found using the formula

A=\frac{1}{2}bh.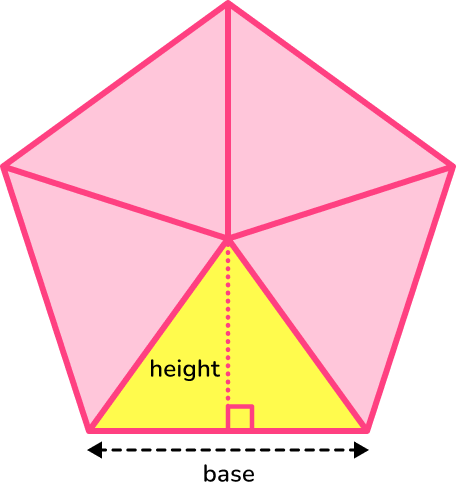

Where $b$ is the base length (or the side of the pentagon) and $h$ is the perpendicular height of the triangle. Sometimes these values need to be calculated.

Step-by-step guide: Area of a triangle

This means the area of a regular pentagon can also be written as

\text{Area of regular pentagon}=5\times \frac{1}{2}bh.

● Angles in a regular pentagon

We can work out the angles of a regular polygon to answer a variety of different area questions.

Splitting the regular pentagon into $5$ congruent isosceles triangles, we can use the angle fact that the sum of angles at a point is $360^{\circ}$ to work out the angle at the top of the isosceles triangle.

360\div 5=72^{\circ}

The equal base angles can be found by using the angle fact that the sum of angles in a triangle is $180^{\circ}.$

(180-72)\div 2=54^{\circ}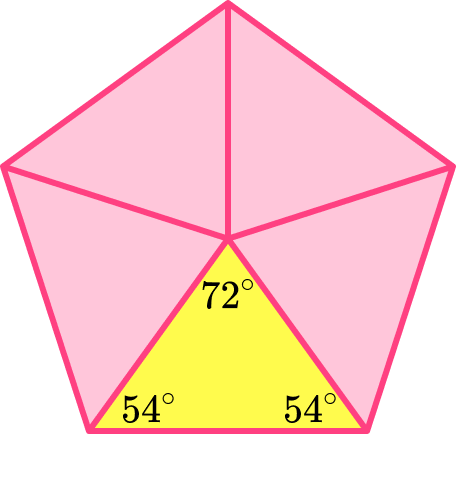

Step-by-step guide: Interior angles of a polygon

Step-by-step guide: Angles types

Step-by-step guide: Area of an isosceles triangle

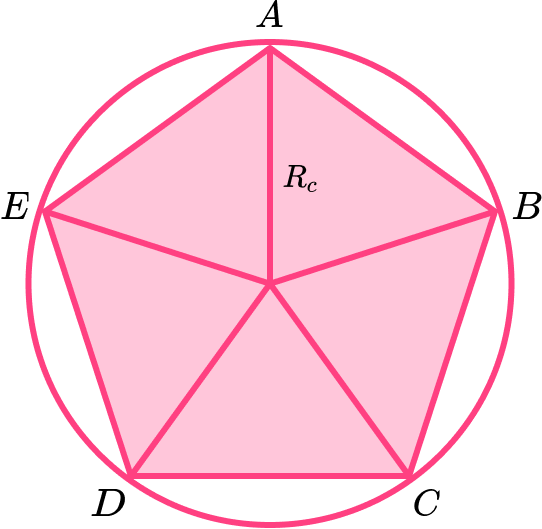
● The radii of a regular pentagon

A regular pentagon has two radii.

The apothem is the radius of the inscribed circle, $R_i.$

The radius of the inscribed circle is perpendicular to the sides of the regular pentagon and meets the side at the midpoint.

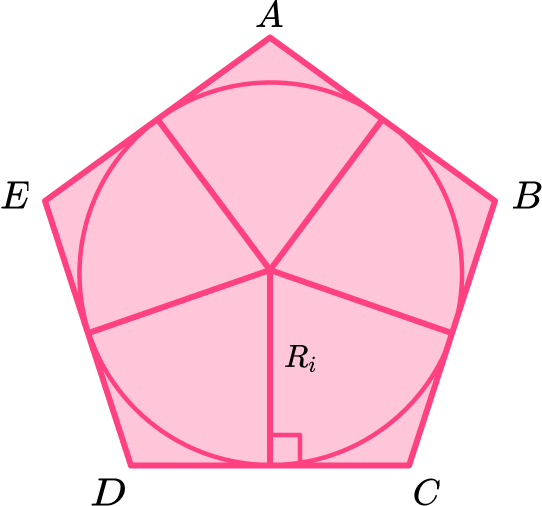
When a regular pentagon is drawn within a circle the circle is known as the circumcircle and the radius is $R_c.$

● Area formula using the perimeter and apothem of a pentagon

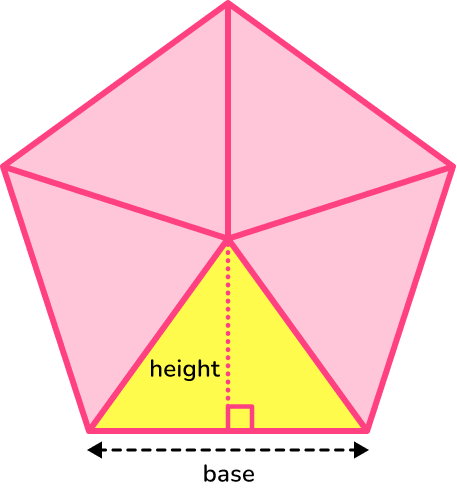
The height (or inscribed radius) in this regular pentagon is also known as the apothem of the pentagon.

We can use this formula to find the area of a regular pentagon,

\text{Area of regular pentagon}= \frac{1}{2}\times \text{perimeter}\times \text{apothem}.

The perimeter of the pentagon can be found by multiplying the side length by $5.$

You are not expected to know this formula at GCSE.

How to solve an area of a pentagon problem

In order to solve an area of a pentagon problem:

Consider the pentagon as a compound shape and split it appropriately.
Calculate the area of the parts.
Calculate the total area of the pentagon.
Write the answer, including the correct units.

How to solve an area of a pentagon problem

Area worksheet (includes area of a pentagon)

Get your free area of a pentagon worksheet of 20+ area questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area worksheet (includes area of a pentagon)

Get your free area of a pentagon worksheet of 20+ area questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on area

Area of a pentagon is part of our series of lessons to support revision on area. You may find it helpful to start with the main area lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Area of a pentagon examples

Example 1: area of an irregular pentagon formed with one triangle and a rectangle

$\text{ABCDE}$ is a pentagon.

Calculate the area of the pentagon.

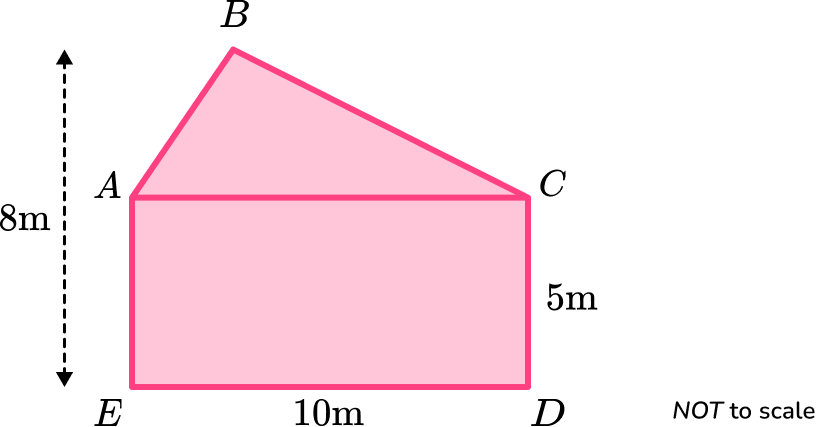
Consider the pentagon as a compound shape and split it appropriately.

The diagram given in the question is already split into a rectangle and a triangle.

2Calculate the area of the parts.

Find the area of the triangle $\text{ABC}.$

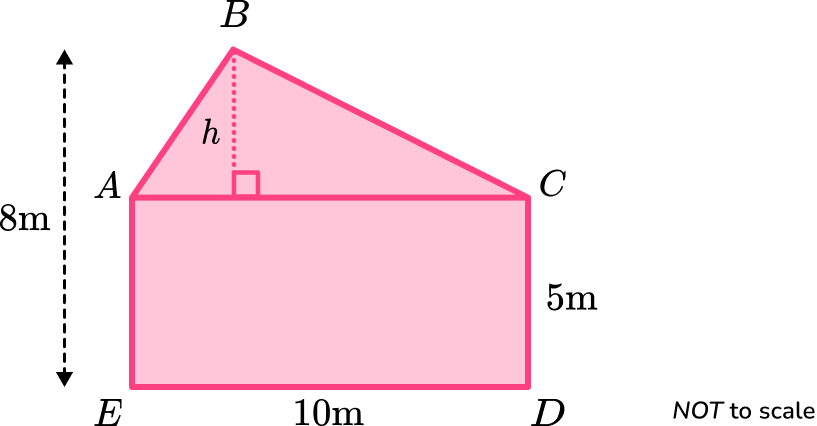
The height of the triangle, $h,$ is

h=8-5=3.

Therefore the area of the triangle is

A=\frac{1}{2}bh=\frac{1}{2}\times 10\times 3=15.

The area of the rectangle $\text{ACDE}$ is

A=bh=10\times 5=50.

3Calculate the total area of the pentagon.

The total area of the pentagon is found by adding the area of the triangle and the area of the rectangle together.

\text{Total Area}=15+50=65

4Write the answer, including the correct units.

The dimensions of the shape were given in metres, so the units of the area will be in square metres. The area of pentagon $\text{ABCDE}$ is $65 \ m^{2}.$

Example 2: area of an irregular pentagon formed with one isosceles triangle and a rectangle

$\text{ABCDE}$ is a pentagon.

Calculate the area of the pentagon.

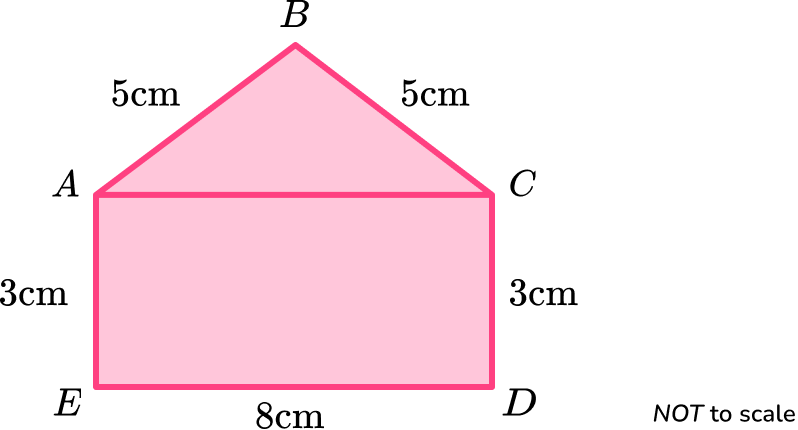
Consider the pentagon as a compound shape and split it appropriately.

The diagram given in the question is already split into a rectangle and a triangle.

Calculate the area of the parts.

Find the area of the triangle $\text{ABC}.$

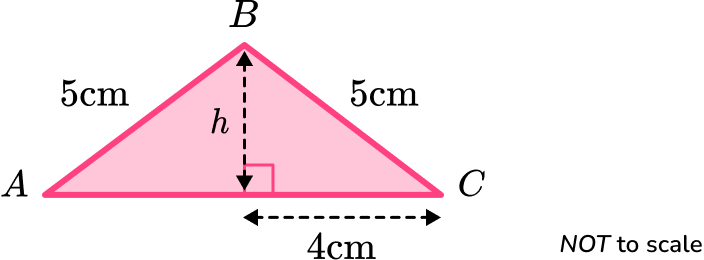
You can find $h$ the height of the triangle by using Pythagoras’ theorem.

$h=\sqrt{5^2-4^2}=3$

Note: The height can also be found as it is part of the $3, 4, 5$ Pythagorean triple.

Therefore the area of the triangle is

$A=\frac{1}{2}bh=\frac{1}{2}\times 8\times 3=12.$

The area of the rectangle $\text{ACDE}$ is

$A=bh=8\times 3=24.$

Calculate the total area of the pentagon.

The total area of the pentagon is found by adding the area of the triangle and the area of the rectangle together.

$\text{Total Area}=12+24=36$

Write the answer, including the correct units.

The dimensions of the shape were given in centimetres, so the units of the area will be in square centimetres. The area of pentagon $\text{ABCDE}$ is $36 \ cm^2.$

Example 3: calculating the area of a regular pentagon given the area of one of the isosceles triangles

Calculate the area of the regular pentagon $\text{ABCDE}$ given that the area of one of the congruent triangles is $20 \ cm^2.$

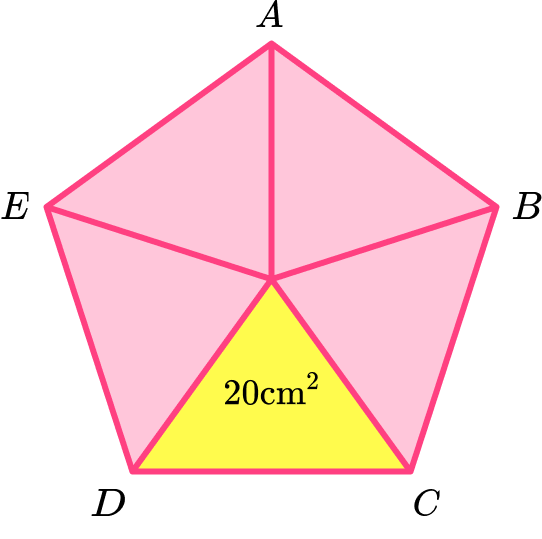
Consider the pentagon as a compound shape and split it appropriately.

The diagram given in the question is already split into five congruent isosceles triangles.

Calculate the area of the parts.

The area of one triangle has been given, $20 \ cm^2.$

Calculate the total area of the pentagon.

The total area of the regular pentagon is

$\begin{aligned} \text{Area of regular pentagon}&=5\times \text{Area of one triangle}\\\\ &=5\times 20\\\\ &=100 \end{aligned}$

Write the answer, including the correct units.

The area of pentagon $\text{ABCDE}$ is $100 \ cm^2.$

Example 4: area of a pentagon given the side length

Calculate the area of the regular pentagon $\text{ABCDE}$ given that the length of one side of the regular pentagon is $10 \ cm.$

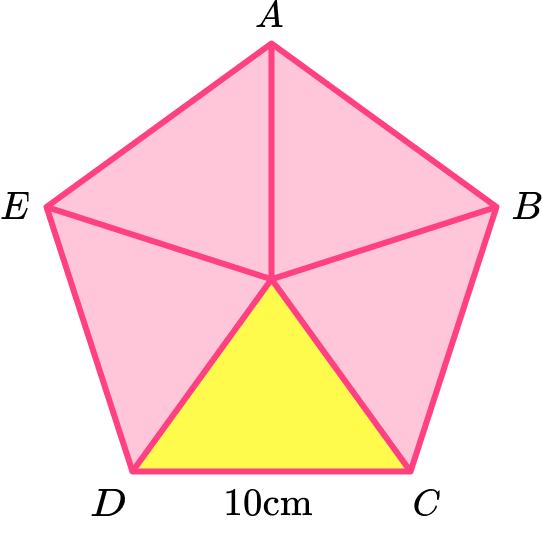
Consider the pentagon as a compound shape and split it appropriately.

Here the regular pentagon $\text{ABCDE}$ has been split into five congruent isosceles triangles.

Calculate the area of the parts.

You can find the area of one of the isosceles triangles by using the side length as the base length of the triangle.

You need to work out the height of the triangle. This can be done using trigonometry and the angles in the triangle.

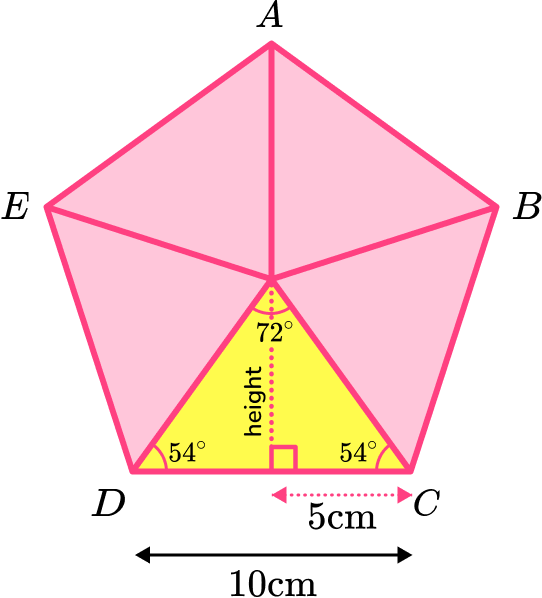
$\text{height}=\tan(54)\times 5=6.8819…$

The area of one of the isosceles triangles is

$\begin{aligned} A&=\frac{1}{2}bh\\\\ &=\frac{1}{2}\times 10\times 6.8819…\\\\ &=34.4095… \end{aligned}$

Calculate the total area of the pentagon.

The total area of the regular pentagon is

$\begin{aligned} \text{Area of regular pentagon}&=5\times \text{area of one triangle}\\\\ &=5\times 34.4095…\\\\ &=172.0477… \end{aligned}$

Write the answer, including the correct units.

The dimensions of the shape were given in centimetres, so the units of the area will be in square centimetres. The area of pentagon $\text{ABCDE}$ is $172 \ cm^2.$

Example 5: area of a pentagon given the height (apothem)

Calculate the area of the regular pentagon $\text{ABCDE}$ given that the length of the apothem of the regular pentagon is $12 \ cm.$

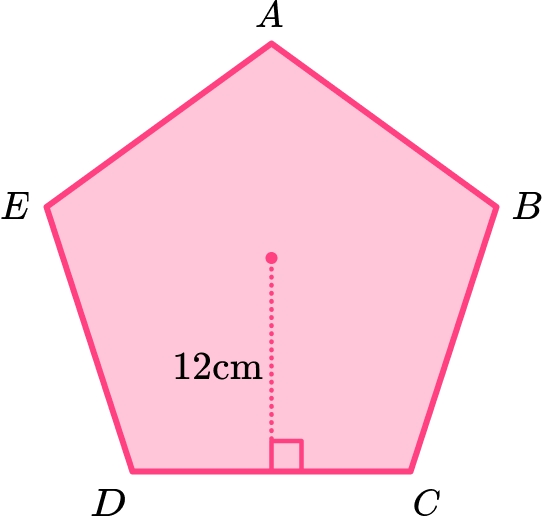
Consider the pentagon as a compound shape and split it appropriately.

Here the regular pentagon $\text{ABCDE}$ has been split into five congruent isosceles triangles.

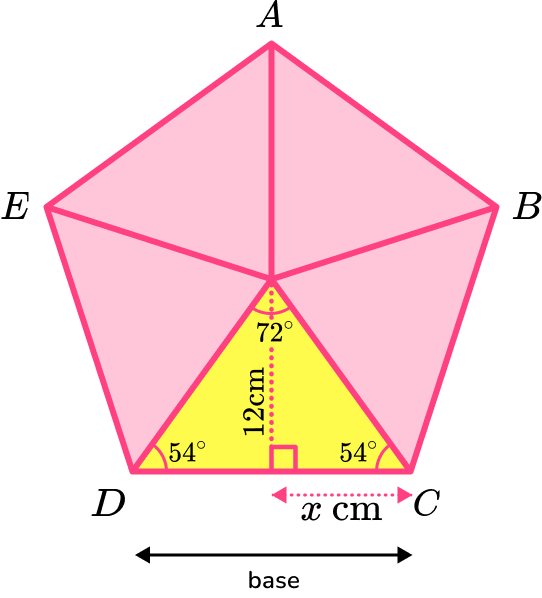
Calculate the area of the parts.

You can find the area of one of the triangles by using the apothem as the perpendicular height of the triangle.

You need to work out the base of the triangle. This can be done using trigonometry and the angles in the isosceles triangle.

$x=12\div \tan(54)=8.7185…$

The base of one of the isosceles triangles is

$\text{base}=2x=2\times 8.7185…=17.4370…$

The area of one of the isosceles triangles is

$\begin{aligned} A&=\frac{1}{2}bh\\\\ &=\frac{1}{2}\times 17.4370…\times 12\\\\ &=104.6221… \end{aligned}$

Calculate the total area of the pentagon.

The total area of the regular pentagon is

$\begin{aligned} \text{Area of regular pentagon}&=5\times \text{area of one triangle}\\\\ &=5\times 104.6221…\\\\ &=523.1106… \end{aligned}$

Write the answer, including the correct units.

The dimensions of the shape were given in centimetres, so the units of the area will be in square centimetres. The area of pentagon $\text{ABCDE}$ is $523 \ cm^2$ (to $3$ significant figures).

Example 6: area of a pentagon given the radius of the circumcircle

Calculate the area of the regular pentagon $\text{ABCDE}$ given that the length from the centre of the pentagon to the vertices is $15 \ cm.$

Consider the pentagon as a compound shape and split it appropriately.

Here is a sketch of the regular pentagon $\text{ABCDE}$ showing the five congruent isosceles triangles.

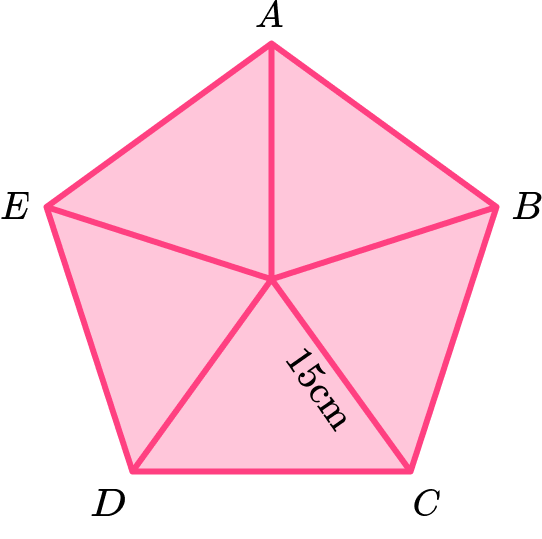
Calculate the area of the parts.

You need to work out the height of the triangle using trigonometry and the angles in the isosceles triangle. The hypotenuse is $15 \ cm.$

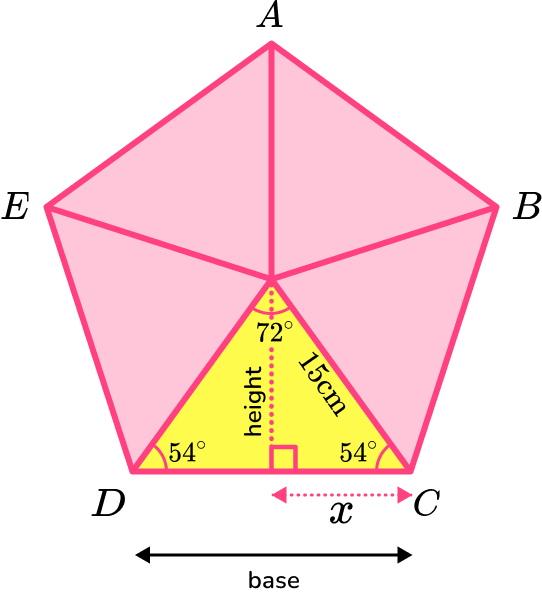
$\text{height}=\sin(54)\times 15=12.13525…$

You need to work out the base of the triangle using trigonometry and the angles in the isosceles triangle. The hypotenuse is $15 \ cm.$

$x=\cos(54) \times 15=8.81677…$

The base of one of the isosceles triangles is

$\text{base}=2x=2\times 8.81677…=17.63355…$

The area of one of the isosceles triangles is

$\begin{aligned} A&=\frac{1}{2}bh\\\\ &=\frac{1}{2}\times 17.63355…\times 12.13525…\\\\ &=106.993… \end{aligned}$

Calculate the total area of the pentagon.

The total area of the regular pentagon is

$\begin{aligned} \text{Area of regular pentagon}&=5\times \text{area of one triangle}\\\\ &=5\times 106.993…\\\\ &=534.96… \end{aligned}$

Write the answer, including the correct units.

The dimensions of the shape were given in centimetres, so the units of the area will be in square centimetres. The area of pentagon $\text{ABCDE}$ is $535 \ cm^2$ (to $3$ significant figures).

Example 7: area of a pentagon given the radius of the circumcircle (diagonals)

Calculate the area of the regular pentagon $\text{ABCDE}$ given that the length from the centre of the pentagon to the vertices is $10 \ cm.$

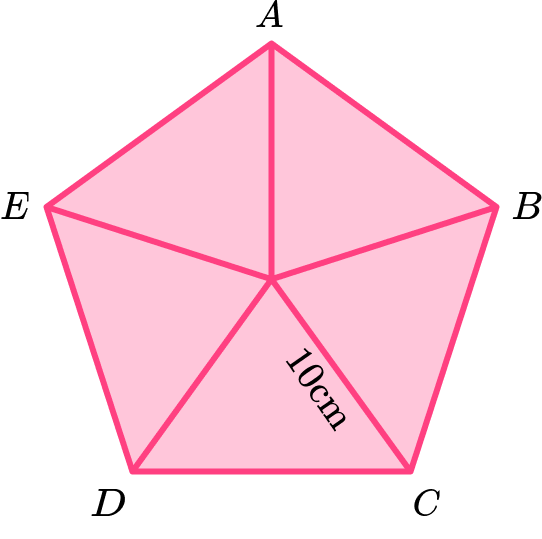
Consider the pentagon as a compound shape and split it appropriately.

The diagram given in the question is already split into five congruent isosceles triangles.

Calculate the area of the parts.

You need to work out the height of the triangle using trigonometry and the angles in the isosceles triangle. You can use HIGHER trigonometry.

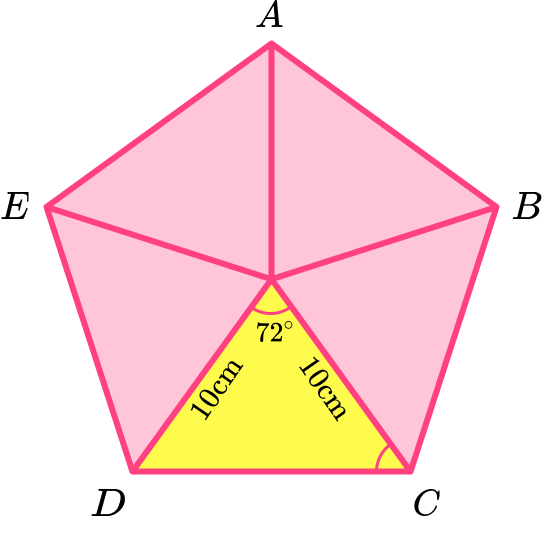
$\begin{aligned} A&= \frac{1}{2}ab \sin C \\\\ &=\frac{1}{2} \times 10\times 10\times \sin (72)\\\\ &=47.5528... \end{aligned}$

Calculate the total area of the pentagon.

The total area of a regular pentagon is

$\begin{aligned} \text{Area of regular pentagon}&=5\times \text{area of one triangle}\\\\ &=5\times 47.5528…\\\\ &=237.764… \end{aligned}$

Write the answer, including the correct units.

The dimensions of the shape were given in centimetres, so the units of the area will be in square centimetres. The area of pentagon $\text{ABCDE}$ is $238 \ cm^2$ (to $3$ significant figures).

Common misconceptions

Using the correct units

Remember that area is measured in square units. Square units include square centimetres $(cm^2),$ square metres $(m^2)$ and square millimetres $(mm^2).$

Don’t round off too early

It is important to not round decimals until the end of the calculation. Rounding too early will result in an inaccurate answer.

Take care of which dimensions you are using

It is important to make sure you keep track of which dimensions you have been given and which dimensions you are calculating. Take care with each step of your calculations and make use of diagrams.

Practice area of a pentagon questions

1050 \ m^2

360 \ m^2

255 \ m^2

202.5 \ m^2

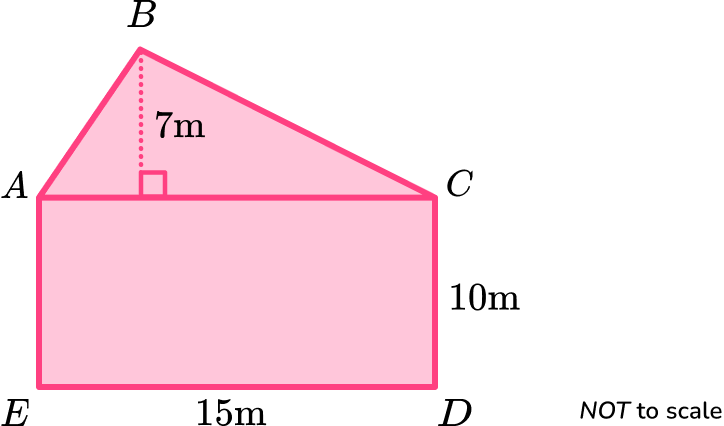
The area of the triangle $\text{ABC}$ is

A=\frac{1}{2}bh=\frac{1}{2}\times 15\times 7=52.5.

The area of the rectangle $\text{ACDE}$ is

A=bh=15\times 10=150.

The total area of the pentagon is found by adding the area of the triangle and the area of the rectangle together.

\text{Total Area}=52.5+150=202.5 \ m^2

1580 \ m^2

1280 \ m^2

1780 \ m^2

1880 \ m^2

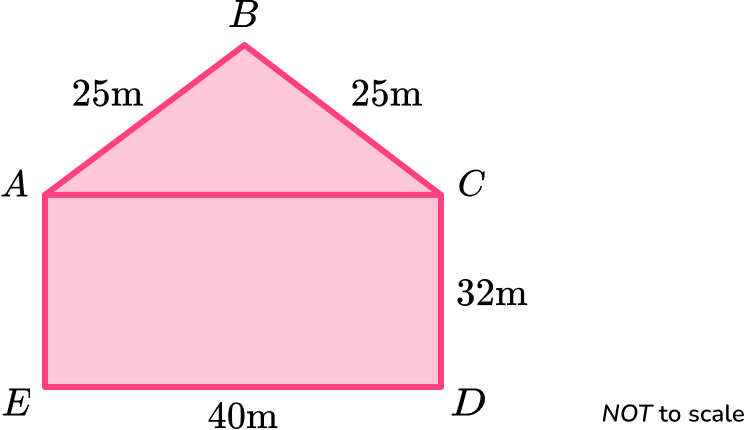
The height of the triangle is

h=\sqrt{25^2-20^2}=15.

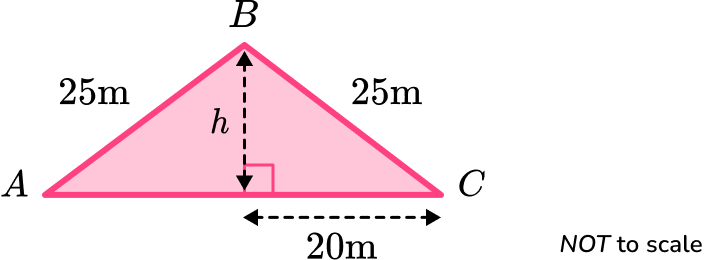
Area of a pentagon question 2 answer

The area of the triangle $\text{ABC}$ is

A=\frac{1}{2}bh=\frac{1}{2}\times 40\times 15=300.

The area of the rectangle $\text{ACDE}$ is

A=bh=40\times 32=1280.

The total area of the pentagon is found by adding the area of the triangle and the area of the rectangle together.

\text{Total Area}=300+1280=1580 \ m^2

3 \ cm^2

60 \ cm^2

75 \ cm^2

100 \ cm^2

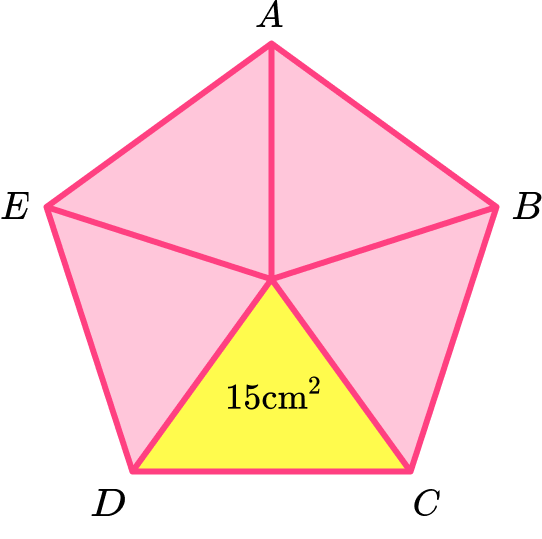
The area of the regular pentagon is

\begin{aligned} & =5 \times \text { area of one triangle } \\\\ & =5 \times 15 \\\\ & =75 \mathrm{~cm}^2 \end{aligned}

1453 \ cm^2

951 \ cm^2

688 \ cm^2

138 \ cm^2

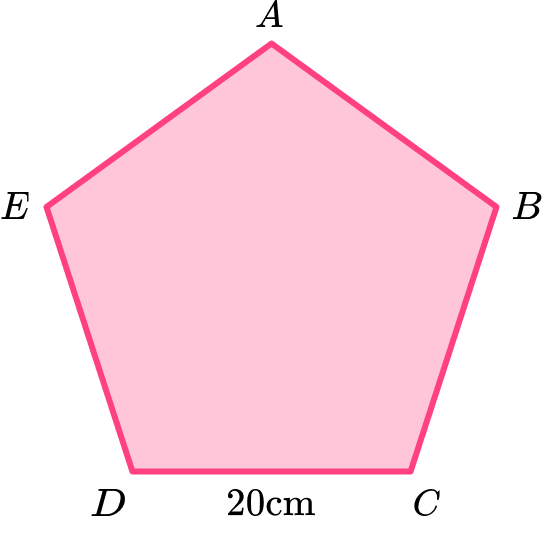
The height of the triangle is

\text{height}=\tan(54)\times 10=13.7638…

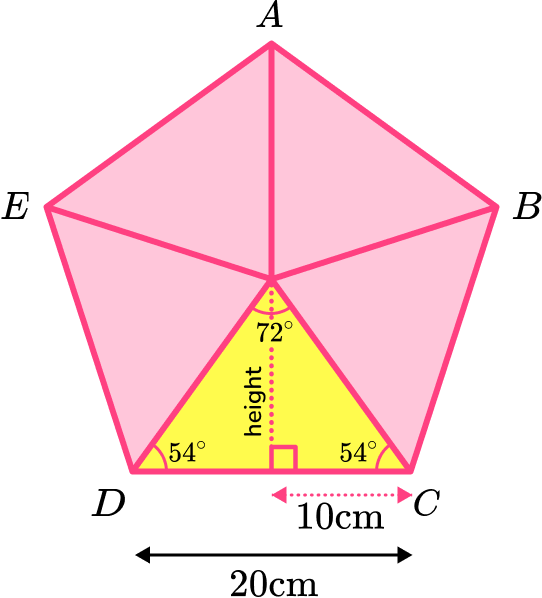
Area of a pentagon question 4 answer

The area of one of the isosceles triangles is

\begin{aligned} A&=\frac{1}{2}bh\\\\ &=\frac{1}{2}\times 20\times 13.7638…\\\\ &=137.638… \end{aligned}

The area of the regular pentagon is

\begin{aligned} & =5 \times \text { area of one triangle } \\\\ & =5 \times 137.638 \\\\ & =688.190… \end{aligned}

The area of the regular pentagon is $688 \ cm^2$ to $3$ significant figures.

2750 \ cm^2

5810 \ cm^2

11011 \ cm^2

3804 \ cm^2

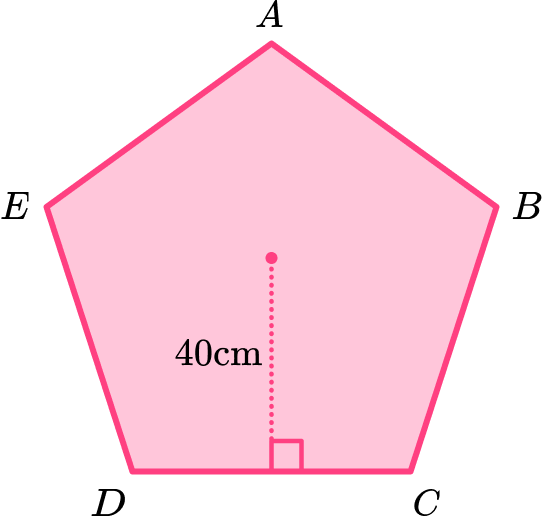
Using trigonometry,

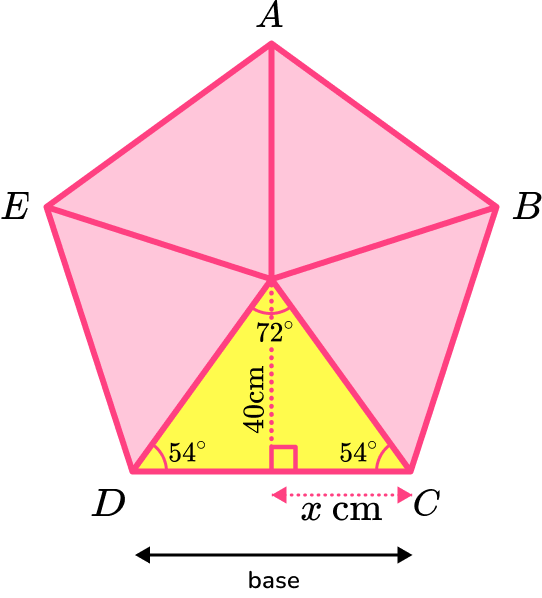
Area of a pentagon question 5 answer

x=40\div \tan(54)=29.0617…

The base of one of the isosceles triangles is

\text{base}=2x=2\times 29.0617…=58.1234…

The area of one of the isosceles triangles is

\begin{aligned} A&=\frac{1}{2}bh\\\\ &=\frac{1}{2}\times 58.1234…\times 40\\\\ &=1162.468… \end{aligned}

The area of the regular pentagon is

\begin{aligned} & =5 \times \text { area of one triangle } \\\\ & =5 \times 1162.468… \\\\ & =5812.34… \end{aligned}

The area of pentagon $\text{ABCDE}$ is $5810 \ cm^2$ to $3$ significant figures.

497 \ cm^2

1050 \ cm^2

687 \ cm^2

137 \ cm^2

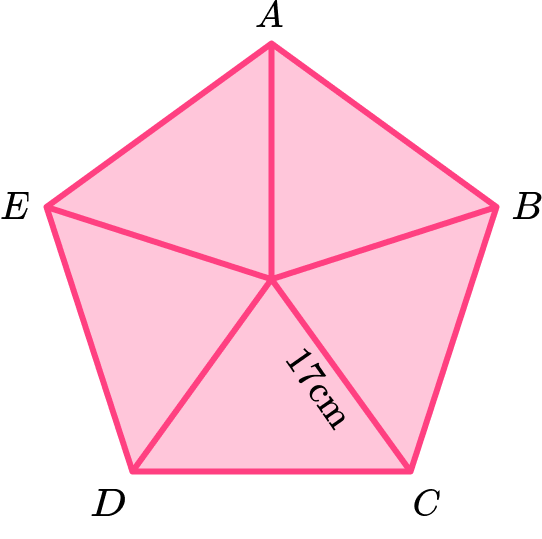
Using trigonometry,

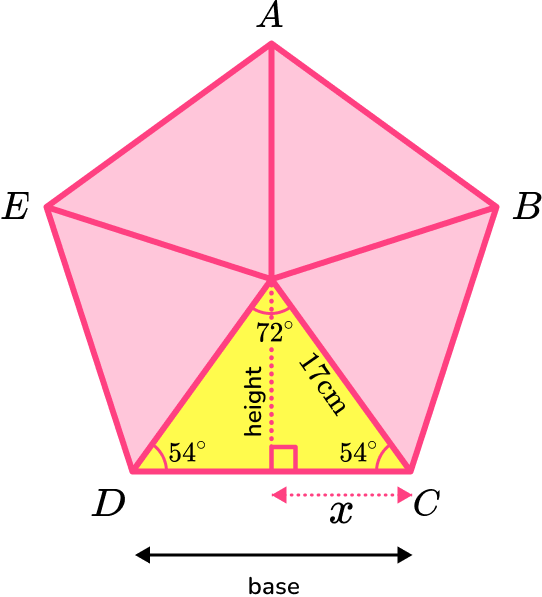
Area of a pentagon question 6 answer

The height of the triangle can be calculated using trigonometry and the angles in the isosceles triangle.

The hypotenuse is $17 \ cm.$

\text{height}=\sin(54)\times 17=13.7532…

You need to work out the base of the triangle using trigonometry.

x=\cos(54) \times 17=9.9923…

The base of one of the isosceles triangles is

\text{base}=2x=2\times 9.9923…=19.9846…

The area of one of the isosceles triangles is

\begin{aligned} A&=\frac{1}{2}bh\\\\ &=\frac{1}{2}\times 19.9846…\times 13.7532…\\\\ &=137.427… \end{aligned}

The area of the regular pentagon is

\begin{aligned} & =5 \times \text { area of one triangle } \\\\ & =5 \times 137.427.. \\\\ & =687.138… \end{aligned}

The area of pentagon $\text{ABCDE}$ is $687 \ cm^2$ to $3$ significant figures.

Area of a pentagon GCSE questions

1. The diagram below shows irregular pentagon $\text{PQRST}.$

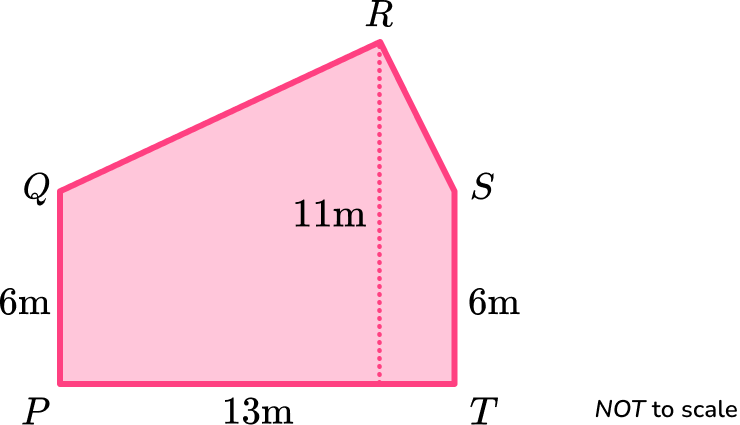
Area of a pentagon GCSE question 1

Calculate the area of the irregular pentagon $\text{PQRST}.$

Give the correct units for your answer.

(4 marks)

Show answer

13 \times 6=78

(1)

\frac{1}{2} \times (11-6) \times 13=32.5

(1)

78+32.5

(1)

110.5 \ m^2

(1)

2. (a) The diagram shows a right-angled triangle
$\text{OAM}.$

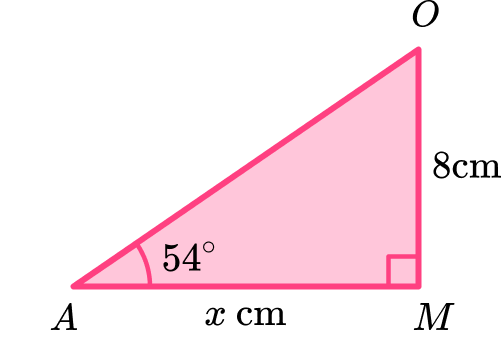
Area of a pentagon GCSE question 1 a

Calculate the value of $x.$

Give your answer correct to $3$ decimal places.

(b) $\text{ABCDE}$ is a regular polygon.

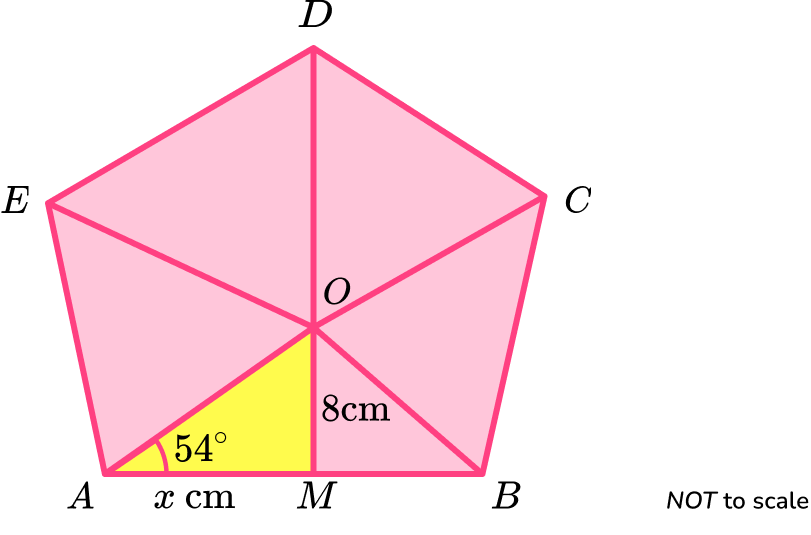
Area of a pentagon GCSE question 1 b

$\text{O}$ is the centre of the regular polygon.

$\text{M}$ is the midpoint of $\text{AB}.$

Use your answer to part (a) to find the area of the regular polygon.

Give your answer correct to $3$ significant figures.

(5 marks)

Show answer

(a)

x=8\div \tan(54)

(1)

5.812 \ cm

(1)

(b)

\frac{1}{2} \times 2 \times 5.812 \times 8=46.49…

(1)

5 \times 46.49…

(1)

232 \ cm^2

(1)

3. A school caretaker wants to draw a regular pentagon on the school playground.

To do this the caretaker starts by drawing a circle with radius $5 \ m.$

He then marks $5$ equidistant points on the circumference of the circle.

He joins the points to make a regular pentagon.

Calculate the area of the regular pentagon.

Give your answer in $m^2$ correct to $3$ significant figures.

(5 marks)

Show answer

$Sin (54) \times 5=(4.045…)$ or $Cos(54) \times 5=(2.938…)$

(1)

Height of isosceles triangle $=5.877\dots$

(1)

Area of isosceles triangle $=11.888\dots$

(1)

5 \times 11.888…

(1)

59.4 \ m^2

(1)

Learning checklist

You have now learned how to:

Find the area of an irregular pentagon using compound areas

Find the area of a regular pentagon

Solve problems involving the area of a regular pentagon

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.