Angles in a triangle

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Types of triangles Angles on a straight line, at a point, right angles and opposite angles Forming and solving equations

This topic is relevant for:

GCSE Maths Geometry and Measure Angles Angles In Polygons

Angles In A Triangle

Here is everything you need to know about angles in a triangle including what the angles in a triangle add up to, how to find missing angles, and how to use this alongside other angle facts to form and solve equations.

There are also angles in a triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are angles in a triangle?

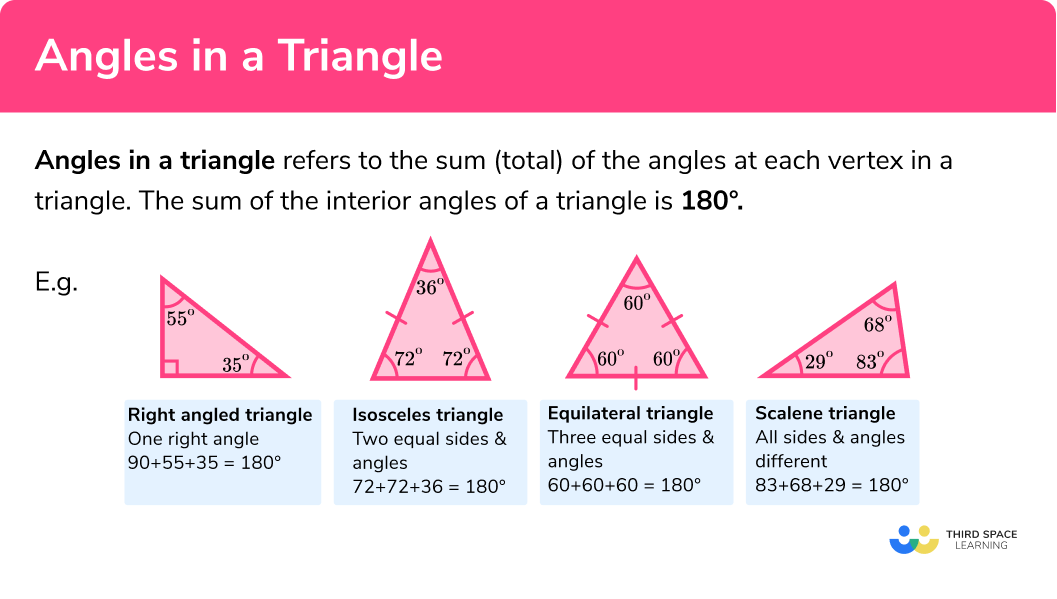
All triangles have interior angles that add up to $180º$ .

Angles in a triangle are the sum (total) of the angles at each vertex in a triangle.

We can use this fact to calculate missing angles by finding the total of the given angles and subtracting it from $180º$ .

This is true for all types of triangles.

Right Angle Triangle: One $90°$ angle, the other two angles will have a total of $90°$ .
Isosceles Triangle: Two equal sides and angles.
Equilateral Triangle: All three angles are $60°$ .
Scalene Triangle: All three angles are different.

Examples:

What are angles in a triangle?

How to find a missing angle in a triangle

In order to find the missing angle in a triangle:

Add up the other angles within the triangle.
Subtract this total from $180º$ .

Explain how to find a missing angle in a triangle in 2 steps

Angles in a triangle worksheet

Get your free angles in a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Angles in a triangle worksheet

Get your free angles in a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on angles in polygons

Angles in a triangle is part of our series of lessons to support revision on angles in polygons. You may find it helpful to start with the main angles in polygons lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Finding missing angles examples

Example 1: scalene triangle

Work out the size of the angle labelled $a$ in the following triangle.

We are given the angles $57º$ and $79º$ . Add these together.

\[57 +79 = 136^{\circ}\]

2Subtract $136º$ from $180º$ .

\[180 – 136 = 44^{\circ}\]

\[a = 44^{\circ}\]

Example 2: right angled triangle

Find the angle labelled $b$ in the following triangle.

We are given the angles $90º$ and $19º$ . Add these together.

\[90 + 19 = 109^{\circ} \]

Subtract $109º$ from $180º$ .

\[180-109=71^{\circ}\]

\[b = 71^{\circ}\]

Example 3: isosceles triangle

Find the angle labelled $c$ in the following triangle.

When two sides of a triangle are equal, the angles at the ends of those sides will also be equal.

We are given the angle $64º.$ As this is an isosceles triangle (two equal length sides and two equal angles), the other angle at the bottom will also be $64º$ .

\[64+64=128^{\circ}\]

Subtract $128º$ from $180º$ .

\[180-128=52^{\circ}\]

\[c = 52^{\circ}\]

How to find one of the two equal angles in an isosceles triangle

Subtract the given angle from $180º$ .
Divide by $2$ .

Example 4: equal angles in an isosceles triangle

Find the size of the angle labelled $d$ in the triangle below.

This is an isosceles triangle. We are given one angle and asked to find one of the remaining two angles, which we know are equal.

\[180-110=70^{\circ}\]

The other two angles in this triangle add up to $70º$ .

Since the other two angles in this triangle are equal, we can find $d$ by dividing by $2$ .

\[70 \div 2=35^{\circ}\]

\[d = 35^{\circ}\]

How to use angle facts to solve problems

Sometimes the problem will involve using other angle facts.
Let’s recap some of the other angle facts we know:

Angles in a Triangle How to use angle facts

Use angle facts to fill in any possible angles.
Use these angles to calculate missing angles in the triangle.

These steps are interchangeable and may need to be repeated for more difficult problems.

Example 5: using angles at a point

Find the size of the angle labelled $e$ .

Here we can use the fact that angles at a point add up to $360º$ .

\[360-310=50^{\circ}\]

Now we know two angles within the triangle, we can find the missing angle.

\[100+50=150\]

\[180-150=30^{\circ}\]

\[e = 30^{\circ}\]

Example 6: using opposite angles

This time we already know two of the angles in the triangle so we can start by finding the third angle.

\[90+61=151\]

\[180-151=29^{\circ}\]

We can use the fact that opposite angles are equal to find $f$ .

\[f = 29^{\circ}\]

Example 7: two different triangles

Find the size of the angle labelled $g$ .

We know two of the angles in the right hand triangle and so we can calculate the third.

\[48+18=66\]

\[180-66=114^{\circ}\]

We can use the fact that angles on a straight line add up to $180º$ .

\[180-114=66^{\circ}\]

Since the sides of the triangle are equal, the left hand triangle is an isosceles triangle and the two angles at the bottom of the triangle are equal. Therefore we can work out the third angle.

\[66+66=132\]

\[180-132=48^{\circ}\]

\[g = 48^{\circ}\]

How to work out angles in a triangle with algebra

We can use the fact that the angles in a triangle add up to $180º$ to form equations which we can then solve to find the values of the angles in the triangle.

Add together the expressions for each angle and simplify.
Put the simplified expression equal to $180º$ .
Solve the equation.
Substitute your value back in to find the angles in the triangle.

Example 8: angles involving algebra

Find the size of each angle in this triangle.

Add the expressions for each angle.

\[4h + 3h + 2h = 9h\]

Put the simplified expression equal to $180º$ .

\[9h = 180\]

Solve the equation.

\[h = 20\]

Work out the angles.

\begin{array}{l} 2 \times 20 = 40\\\\ 3 \times 20 = 60\\\\ 4 \times 20 = 80 \end{array}

The three angles are $40º$ , $60º$ and $80º$ .

Example 9: angles involving algebra

Find the size of each angle in this right-angled triangle.

Add the expressions for each angle.

\[3i + 25 + 2i – 5 + 90 = 5i + 110\]

Put the simplified expression equal to $180º$ .

\[5i + 110 = 180\]

Solve the equation.

\[5i = 70\]

\[i = 14\]

Work out the angles.

\begin{array}{l} 3 \times 14+25=67\\\\ 2 \times 14-5=23 \end{array}

The three angles are $23º$ , $67º$ and $90º$ .

Common misconceptions

Incorrect angle sum

Using $360º$ instead of $180º$ for the sum of the angles of the triangle.

Equal angles in an isosceles triangle

Selecting the wrong angles when identifying the equal angles in an isosceles triangle (particularly a problem when the equal angles are not at the bottom). The angle that is different in an isosceles triangle is the one between the two sides with equal length.

Angles in a Triangle Common Misconceptions

Practice angles in a triangle questions

33^{\circ}

123^{\circ}

57^{\circ}

213^{\circ}

90+57=147

180-147=33^{\circ}

51^{\circ}

258^{\circ}

78^{\circ}

39^{\circ}

This is an isosceles triangle and the two angles at the bottom of the triangle are equal.

51+51=102

180-102=78^{\circ}

42^{\circ}

69^{\circ}

138^{\circ}

48^{\circ}

This is an isosceles triangle and the two angles on the right are equal.

180-42=138

138 \div 2 = 69^{\circ}

60^{\circ}

90^{\circ}

30^{\circ}

180^{\circ}

All three angles in an equilateral triangle are equal so

180 \div 3 = 60^{\circ}

24^{\circ}

156^{\circ}

48^{\circ}

78^{\circ}

The angle opposite $24^{\circ}$ is also $24^{\circ}$ since vertically opposite angles are equal.

The triangle is an isosceles triangle and the two angles on the left are the same size.

180-24=156

156 \div 2 = 78^{\circ}

51^{\circ}

20^{\circ}

129^{\circ}

31^{\circ}

Looking at the left hand triangle frist, we can find the missing angle in that triangle:

90+39=129

180-129=51^{\circ}

We can then use the fact that angles on a straight line add up to $180^{\circ}$ to find the unlabelled angle in the right hand triangle:

180-51=129^{\circ}

Angles in a Triangle Practice question 6 answer

We can then find angle $v$ :

129+31=160^{\circ}

180-160=20^{\circ}

176^{\circ}, 112^{\circ}, 76^{\circ}

102.5^{\circ}, 72.5^{\circ}, 46.25^{\circ}

86^{\circ}, 56^{\circ}, 38^{\circ}

78^{\circ}, 48^{\circ}, 34^{\circ}

Adding the expressions gives us:

2u+20+2u-10+u+5=5u+15

Therefore

\begin{aligned} 5u+15&=180\\\\ 5u&=165\\\\ u&=33^{\circ} \end{aligned}

2 × 33+20=86^{\circ}

2 × 33-10=56^{\circ}

33+5=38^{\circ}

Angles in a triangle GCSE questions

1. Find the size of angle $x$ given that the exterior angle shown is $153^{\circ}$ .

Angles in a Triangle exam question 1

(2 marks)

Show answer

180-153=27^{\circ}

(1)

90 + 27 = 177

180-117=63^{\circ}

(1)

2. (a) Calculate the size of angle $ACE$ .

(b) Show that $BCD$ is an isosceles triangle.

(5 marks)

Show answer

(a)

$90 + 36 = 126$

(1)

$180-126=54^{\circ}$

(1)

(b)

Angle $CBD$ :

$= 180 - 117$

$=63^{\circ}$

Angle $BDC$ :

$63 + 54 = 117$

$180-117=63^{\circ}$

(1)

Two angles equal therefore isosceles

(1)

3. Work out the size of the smallest angle in the right angled triangle.

Angles in a Triangle exam question 3

(4 marks)

Show answer

$3x - 10 + 2x + 55 + 90 (= 5x + 135)$

(1)

$5x + 135 = 180$

(1)

$x = 9$

(1)

$3\times 9-10=17^{\circ}$

(1)

Learning checklist:

You have now learned how to:

Use the sum of the angles of a triangle to find missing angles

Apply other angle facts to find missing angles in triangle problems

Form and solve equations using the sum of the angles in a triangle

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.