Maths formulas

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Arithmetic Decimals Fractions Substitution Negative numbers Expanding brackets Factorising

This topic is relevant for:

GCSE Maths Algebra

Maths Formulas

Here we will learn about maths formulas, including what maths formulas are, how to use them and how to rearrange them. We will also look at special formulas involved in kinematics.

There are also maths formulas worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are maths formulas?

Maths formulas are rules that are written connecting two or more variables. We can use maths formulas to work out the values of given variables, based on other known values.

To do this we substitute the values that we know into the formula and then calculate the value of the unknown.

For example, here is a rectangle with base $b$ and height $h.$

The formula for the perimeter $P$ of a rectangle is

P=2(b+h).

We can use this formula to find the value of the perimeter by substituting in the values for the base and height of the rectangle.

Other examples of maths formulas you may recognise include,

A=\pi r^2, \quad \quad s=\frac{d}{t}, \quad \quad V=\frac{1}{3}\pi r^2 h, \quad \quad sin(\theta)=\frac{O}{H}.

What are maths formulas?

List of maths formula

These are the maths formulas you are most likely to encounter for GCSE.

Areas

Area of a parallelogram

$A=bh \hspace{1.5cm}$ Where $A$ is Area, $b$ is base and $h$ is height.

Area of a triangle

$A=\frac{1}{2}bh \hspace{1.35cm}$ Where $A$ is Area, $b$ is base and $h$ is height.

Area of a trapezium

$A=\frac{1}{2}(a+b)h \hspace{.65cm}$ Where $A$ is Area, $a$ and $b$ are the parallel sides and $h$ is height.

Circles

Circumference of a circle

$C=\pi d \hspace{1.6cm}$ Where $C$ is circumference and $d$ is diameter.

Area of a circle

$A=\pi r^2 \hspace{1.55cm}$ Where $A$ is Area and $r$ is radius.

These formulas can be extended to give the following

$\text{Arc length}=\frac{\theta}{360}\pi d \;\;$ and $\;\; \text{Sector area}=\frac{\theta}{360}\pi r^2$

Where $\theta$ is the angle at the centre of the sector.

Volumes:

Volume of a cuboid:

$V=lwh \hspace{1cm}$ Where $V$ is volume, and $l,w$ and $h$ are the lengths of the $3$ sides.

Volume of a prism:

V=\text{area of cross}-\text{section}\times \text{length}

Volume of a cylinder:

$V=\pi r^2 h \hspace{1cm}$ Where $V$ is volume, $r$ is radius and $h$ is height.

Angles in a polygon:

Sum of angles in a polygon:

$S=180(n-2) \hspace{.5cm}$ Where $S$ is sum and $n$ is number of sides.

Compound measures:

Speed, distance, time

$s=\frac{d}{t} \hspace{1.5cm}$ Where $s$ is speed, $d$ is distance and $t$ is time.

Mass, density, volume

$d=\frac{m}{v} \hspace{1.4cm}$ Where $m$ is mass, $d$ is density and $v$ is volume.

Right-angled triangles:

Pythagoras’ theorem

a^2+b^2=c^2

Where $c$ is the hypotenuse and $a$ and $b$ are the shorter sides of a right-angled triangle.

Trigonometry

\sin(\theta)=\frac{O}{H}. \hspace{1cm} \cos(\theta)=\frac{A}{H}. \hspace{1cm} \tan(\theta)=\frac{O}{A}.

Where $O$ is the opposite side, $A$ is the adjacent side and $H$ is the hypotenuse.

Some formulas are for the Higher GCSE.

Quadratic formula:

x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}

Where $a,b$ and $c$ are coefficients of the quadratic equation to solve $ax^2+bx+c=0.$

Pyramids, Cones and Spheres

Volume of a pyramid

$V=\frac{1}{3}\times \text{area of base} \times h \hspace{1cm}$ Where $V$ is volume and $h$ is height.

Volume of a cone

$V=\frac{1}{3}\pi r^2 h \hspace{1cm}$ Where $V$ is volume, $r$ is radius and $h$ is height.

Curved surface area of a cone

$\text{CSA}=\pi rl \hspace{1cm}$ Where $l$ is the slant length.

Volume of a sphere

$V=\frac{4}{3}\pi r^3 \hspace{1.25cm}$ Where $V$ is volume and $r$ is radius.

Surface area of a cone

\text{SA}=4\pi r^2

Higher Trigonometry:

Area of a triangle

A=\frac{1}{2}ab \sin(C)

Sine rule

\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}

Cosine rule

a^2=b^2+c^2-2bc \cos(A)

Where $a,b$ and $c$ are the sides of a triangle and $A,B$ and $C$ are the corresponding angles.

Coordinate geometry:

Gradient is

m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}

Where $m$ is the gradient and $(x_{1},y_{1})$ and $(x_{2},y_{2})$ are coordinates.

Midpoint of two points is

(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2})

The equation of a straight line is

y-y_{1}=m(x-x_{1})

Using maths formulas

We can use maths formulas in a variety of ways.

For example, looking back to the rectangle above, we had the formula

P=2(b+h).

If we are given $2$ of the values, we can use the formula to work out the third value.

Let’s look at a specific example.

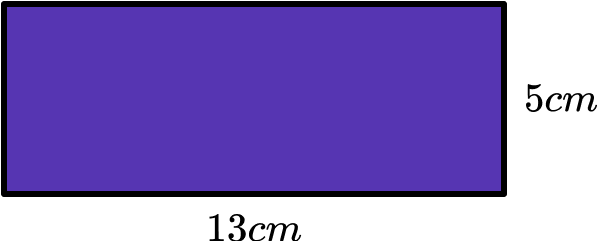
Here $b=13$ and $h=5$ so using the formula for perimeter we can write,

\begin{aligned} P&=2(b+h)\\\\ P&=2(13+5)\\\\ P&=2\times 18\\\\ P&=36 \end{aligned}

We have calculated that the perimeter of the rectangle is $36cm.$

How to use maths formulas

Rearranging formulas

Formulas can be rearranged in a similar way to equations.

To do this, we use inverse operations to make one chosen variable the subject of the formula. The subject of the formula is the single variable that is equal to everything else. i.e. the term by itself on one side of the equal sign.

For example, let’s rearrange $P=2(b+h)$ to make $h$ the subject.

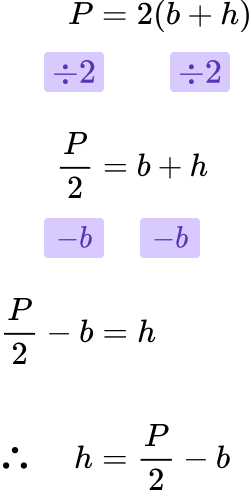
Step-by-step guide: Rearranging formulae

Kinematics formulas

Many of the formulas used at GCSE are about geometrical situations, for example to calculate area or perimeter. However, there are some formulas which are used to solve problems involving moving objects. Kinematics is the maths concerned with the movement of objects.

The $5$ different kinematic formulas involve $5$ different variables of motion.

The variables of motion are,

$s=$ displacement

$u=$ initial velocity

$v=$ final velocity

$a=$ acceleration

$t=$ time

Velocity is speed in a given direction.

Displacement is the distance from the original position.

The five formulas are,

\begin{aligned} &v=u+at \\\\ &s=ut+\frac{1}{2}at^2 \\\\ &s=\frac{1}{2}(u+v)t \\\\ &v^2=u^2+2as \\\\ &s=vt-\frac{1}{2}at^2 \end{aligned}

The kinematic formulas are sometimes known as the suvat equations.

Step-by-step guide: Kinematic formulae

How to use maths formulas

In order to work with maths formulas:

Use the formula given in the question.
Work carefully to answer the question, one step at a time.
Write the final answer clearly.

Explain how to use maths formulas

GCSE maths formulas sheet

Get your free formula sheet containing all of the formulas you need for GCSE maths at foundation and higher.

DOWNLOAD FREE

GCSE maths formulas sheet

Get your free formula sheet containing all of the formulas you need for GCSE maths at foundation and higher.

DOWNLOAD FREE

Maths formulas examples

Example 1: using a maths formula

Given that $F=\frac{9}{5}C+32$ find $F$ when $C=50.$

Use the formula given in the question.

The formula in the question is,

F=\frac{9}{5}C+32.

2Work carefully to answer the question, one step at a time.

Substitute the value that you know into the formula and work out the answer.

Here you know $C=50.$

\begin{aligned} F&=\frac{9}{5}C+32 \\\\ F&=\frac{9}{5}\times 50+32 \\\\ F&=90+32 \\\\ F&=122 \end{aligned}

3Write the final answer clearly.

The answer is $F=122.$

Example 2: using a maths formula

Given that $D=\frac{M}{V},$ calculate $M$ when $D=10$ and $V=40.$

Use the formula given in the question.

The formula in the question is

$D=\frac{M}{V}.$

Work carefully to answer the question, one step at a time.

This time you are given that $D=10$ and $V=40.$ You can substitute these into the formula and then solve to find $M.$

$\begin{aligned} D&=\frac{M}{V}\\\\ 10&=\frac{M}{40}\\\\ 10 \times 40 &=M\\\\ 400&=M \end{aligned}$

Write the final answer clearly.

The answer is $M=400.$

Example 3: rearranging equations

Make $b$ the subject of the formula $w=3ab+2$ .

Use the formula given in the question.

The formula in the question is

$w=3ab+2 .$

Work carefully to answer the question, one step at a time.

Rearrange the formula using inverse operations, one step at a time.

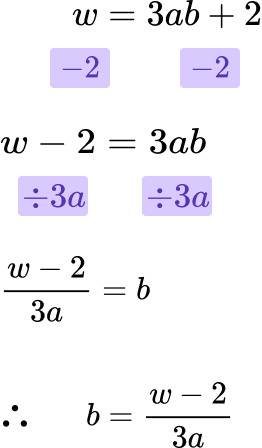
Write the final answer clearly.

The final answer is

$b=\frac{w-2}{3a}$ .

Example 4: kinematics

A train starts from rest and accelerates at $2 \ m/s^{2}.$ Find its velocity after $20$ seconds.

You may use $v=u+at$ where

$t=$ time $\quad \quad \quad \quad \quad \quad u=$ initial velocity

$a=$ acceleration $\quad \quad \quad v=$ final velocity

Use the formula given in the question.

The formula given is

$v=u+at.$

Work carefully to answer the question, one step at a time.

You need to substitute the values into the formula and calculate the answer. The phrase starting at rest indicates that the initial velocity will be $0.$

When answering kinematics questions, it can be helpful to start by writing down what you know.

Here you know that $u=0, \ a=2$ and $t=20.$

$\begin{aligned} v&=u+at \\\\ v&=0+2\times 20 \\\\ v&=40 \end{aligned}$

Write the final answer clearly.

The final answer is $40 \ m/s.$ The units are consistent with the values in the original situation.

Common misconceptions

Take care with writing variables clearly

Neat writing is important. For example, the variables $v$ and $u$ can easily be muddled as they look similar and they both represent velocity in kinematic formulas.

When we square root a number/variable the answer can be positive or negative

The square root of any value can be positive or negative. When taking a square root, use the plus/minus sign $\pm$ to indicate this.

For example,

$\begin{aligned} x^2&=ab-c \\\\ x&=\pm \sqrt{ab-c} \end{aligned}$

Practice maths formulas questions

A=68

A=120

A=240

A=17

Substitute the values into the formula and calculate the answer.

\begin{aligned} A&= \frac{1}{2}bh \\\\ A&= \frac{1}{2}\times 24\times 10\\\\ A&=120 \end{aligned}

H=28

H=8

H=68

H=43

Substitute the values into the formula and calculate the answer.

\begin{aligned} W&=\frac{H}{A}+5\\\\ 12&=\frac{H}{4}+5\\\\ 7&=\frac{H}{4}\\\\ 28&=H \end{aligned}

t=\frac{h-3}{y}

t=\frac{h+3}{y}

t=\frac{h+y}{3}

t=\frac{h-y}{3}

Rearrange using inverse operations.

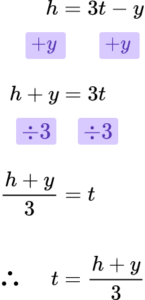
Maths formulas practice question 3 explanation

x=3a+b

x=3a-b

x=3(a-b)

x=3(a+b)

Rearrange using inverse operations.

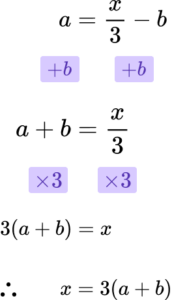
Maths formulas practice question 4 explanation

s=57.5

s=12.5

s=87.5

s=42.5

Substitute the values into the formula and calculate the answer.

\begin{aligned} s&=ut+\frac{1}{2}at^2\\\\ s&= 10\times 5+\frac{1}{2}\times 3 \times 5^2\\\\ s&= 50+37.5\\\\ s&=87.5 \end{aligned}

64 \ m

160 \ m

124 \ m

100 \ m

Substitute the given values into the formula. Note that $a=-6$ because the train is slowing down.

\begin{aligned} s&=ut+\frac{1}{2}at^2 \\\\ s&=28\times 4+\frac{1}{2}\times (-6) \times4^2 \\\\ s&=112-48 \\\\ s&=64 \end{aligned}

The answer will be $64$ metres, as metres is consistent with the other units in the question.

Maths formulas GCSE questions

1. Which of these is a formula. Circle your answer.

\begin{aligned} &\hspace{0.6cm} A \hspace{2.1cm} B \hspace{2.1cm} C \hspace{2cm} D \\ &3x+5=19 \quad \quad 3x=2x+x \quad \quad x=3(a+b) \quad \quad x^2-3x \end{aligned}

(1 mark)

Show answer

$C$ is the formula.

(1)

( $A$ is an equation, $B$ is an identity, $D$ is an expression.)

2. Rearrange $x=my-8$ to make $y$ the subject.

(2 marks)

Show answer

x+8=my

(1)

y=\frac{x+8}{m}

(1)

3. For the following question you may use the formula $v=u+at$ where

$v=$ final velocity $\quad \quad \quad u=$ initial velocity

$a=$ acceleration $\quad \quad \quad \ t=$ time

A motorbike is travelling along a road at a velocity of $11 \ m/s.$ The motorbike accelerates at $3 \ m/s^2$ for $4$ seconds. Find the final velocity.

(2 marks)

Show answer

v=11+3\times 4

(1)

v=23 \ m/s

(1)

Learning checklist

You have now learned how to:

Use mathematical formula

Rearrange equations and formula

Use kinematic formulas

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.