GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Linear equations BIDMAS Simplifying expressions Collecting like terms Factorising single brackets Expanding brackets Trigonometry Dividing fractions Fractions of amounts Area and circumference of a circleThis topic is relevant for:

Changing The Subject Of A Formula
Here we will learn about changing the subject of a formula, including understanding and using inverse operations on standard mathematical formulae to change the subject.
There are also changing the subject of a formula worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is changing the subject of a formula?
Changing the subject of a formula is a way of rearranging a formula to determine a missing quantity in terms of other quantities. This is exactly the same process we apply to solving equations; however to solve an equation, we usually work with one variable and numerical values.
Changing the subject of a formula can also be called rearranging formulae or changing the subject of an equation.

To change the subject of a formula we need to use inverse operations.
For example, Freya is x years old. Geoff is 4 years older than Freya. Harriet is half of Geoff’s age. Write an expression for Harriet’s age.
Let’s start by expressing Freya’s age as x.
As Geoff is 4 years older than Freya, we need to add 4 to Freya’s age.
The expression for Geoff’s age is x+4.
As Harriet is half of Geoff’s age, we need to divide Geoff’s age by 2.
The expression for Harriet’s age is \frac{x+4}{2} or (x+4)\div{2}.
Harriet’s age is \frac{x+4}{2}.
Notice that Harriet’s age is not written as x+4\div{2} as this would simplify to the expression x+2 due to the rules of BIDMAS (order of operations). Instead, (x+4) must be divided by 2, leaving us with the expression for Harriet’s age \frac{x+4}{2}.
We can write this using a function machine,

If we wanted to reverse the process, we would carry out the inverse of each operation of each function to return from Harriet’s age, back to Freya’s age.
(Notice the arrows are now pointing left as we start with Harriet).

Step-by-step guide: Forming expressions (coming soon)
We can also use the method of balancing the formula in order to change the subject.
As inverse operations are important for changing the subject of a formula, below is a table that describes each operation that we will be using along with their mathematical inverse.
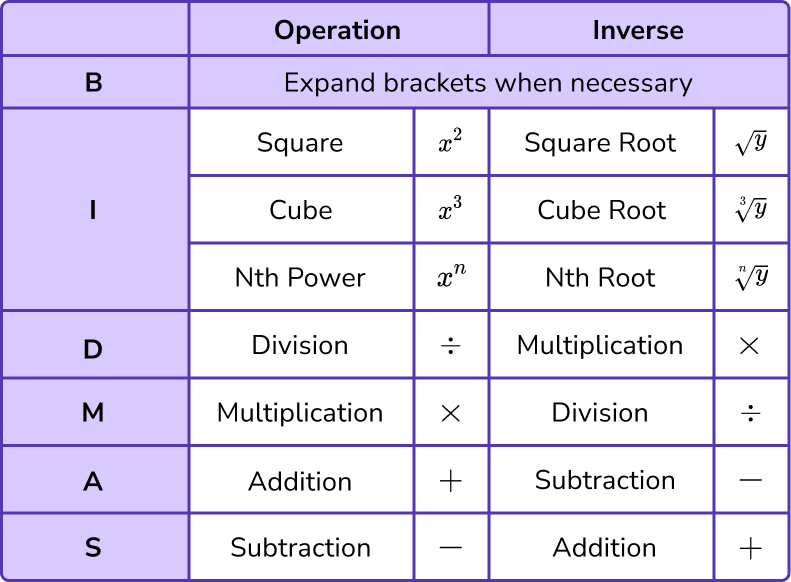
What is changing the subject of a formula?

How to change the subject of a formula
In order to change the subject of a formula:
- Use inverse operations to move a number, term, or variable.
- Repeat this process until the remaining variable is the subject.
Explain how to change the subject of a formula

Changing the subject of a formula worksheet

Get your free changing the subject of a formula worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Changing the subject of a formula worksheet

Get your free changing the subject of a formula worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on maths formulas
Changing the subject of a formula is part of our series of lessons to support revision on maths formulas. You may find it helpful to start with the main maths formulas lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Changing the subject of a formula examples
Example 1: straight line graphs
Make y the subject of the formula, 2x+3y=12. Write your answer in the form y=\frac{a}{b}x+c where a, \ b, and c are integers.
- Use inverse operations to move a number, term, or variable.
We need to subtract 2x from the left hand side of the formula and so we must subtract 2x from the right hand side of the formula as well so it is balanced.
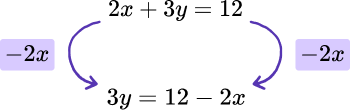
2Repeat this process until the remaining variable is the subject.
As 3y=3\times{y}, we need to divide each side of the equals sign by 3 to cancel out the multiply by 3. This gives us
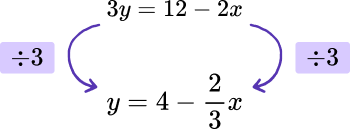
Writing the formula in the form given in the question, we have
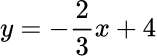
where a=-2, \ b=3 and c=4.
Example 2: iteration
Show that the iterative formula u_{n+1}=\frac{5u_{n}^{2}+2}{3} can be rearranged to give
u_{n}=\sqrt{\frac{3u_{n+1}-2}{5}}.Use inverse operations to move a number, term, or variable.
As u_{n} is ‘trapped’ by the denominator, we need to remove the denominator of the fraction first. As the denominator of a fraction is a division, multiplying both sides of the iterative formula by 3 will cancel out the denominator, leaving us with
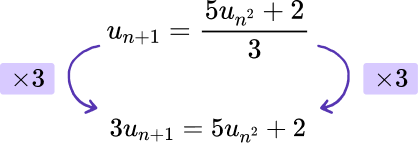
Repeat this process until the remaining variable is the subject.
If we formed the expression 5x+2 using a function machine, we would get

This means that when we use inverse operations, we need to subtract 2 from the expression first, and then divide by 5 to give us the value of x.

Using this in the question, we need to subtract 2 from both sides of the iterative formula, and then divide both sides by 5
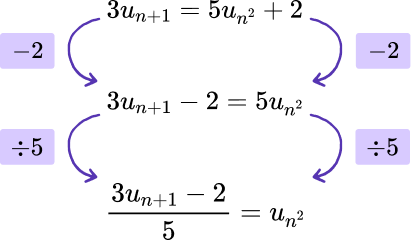
This leaves us with the subject of the formula u_{n}^{2}. As we want the subject to be u_{n}, we need to carry out the inverse operation to the square of a number. This is the square root.
We therefore need to square root both sides of the iterative formula, leaving us with the solution.
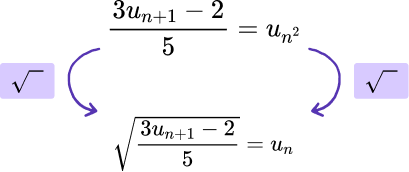
Example 3: calculations with fractions
Given that \frac{a}{b}+\frac{c}{d}=e, rearrange the formula to make a the subject. Write your solution as a single fraction.
Use inverse operations to move a number, term, or variable.
As we want a to be the subject of the formula, we can remove + \frac{c}{d} from the left hand side of the equation by subtracting it from both sides.
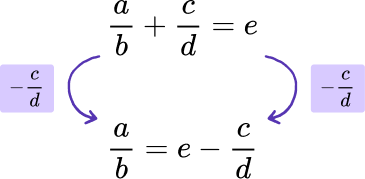
Repeat this process until the remaining variable is the subject.
To remove the denominator b from the fraction \frac{a}{b}, we need to multiply both sides by b.
As we are multiplying the entire of the right hand side by b we can express this within a bracket, and then expand the bracket to get

The question asks us to write the solution as a single fraction and so we need the two terms be and \frac{bc}{d} to have a common denominator. To do this, we multiply be by \frac{d}{d} to get \frac{bde}{d}.
As the two fractions \frac{bde}{d} and \frac{bc}{d} have a common denominator, we can simply subtract the numerators to get
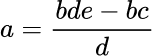
Example 4: area of a sector
The area of a sector S can be calculated using the formula \frac{\theta}{360}\times\pi{r}^{2}=S where r is the radius of the sector.
Make r the new subject of the formula.
Use inverse operations to move a number, term, or variable.
The formula \frac{\theta}{360}\times\pi{r}^{2}=S could be written as the single fraction \frac{\theta\pi{r}^{2}}{360}=S and so we can remove the denominator (360) straight away by multiplying both sides of the formula by 360.
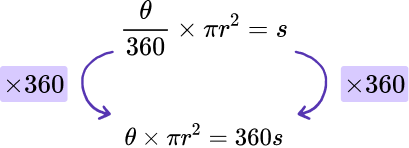
Repeat this process until the remaining variable is the subject.
As \theta\times\pi{r}^{2} is the same as \pi{r}^{2}\times\theta, we can divide both sides of the formula by \theta to get
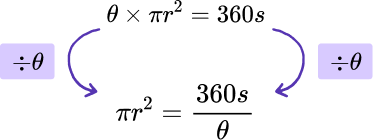
As \pi r^2 is the same as \pi \times r^2 we can divide both sides of the formula by \pi to remove \pi from the left hand side.
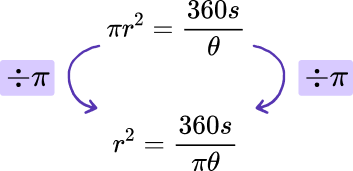
Currently r^2 is the subject of the formula. As we want r to be the subject, we need to square root both sides of the formula to get
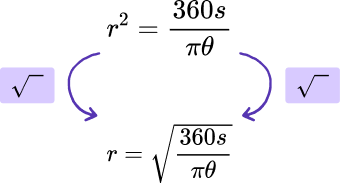
Why does this help me?
By making r the subject of the formula \frac{\theta}{360}\times\pi{r}^{2}=S we can determine the radius of a sector when we know the angle \theta and the area of the sector, S.
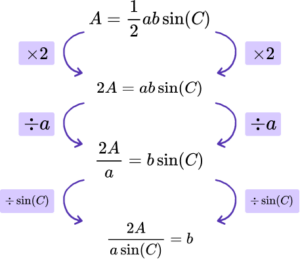
Example 5: area using the sine rule
The area A of a triangle can be calculated using the sine rule
A=\frac{1}{2}ab\sin(C)where C is the included angle between the two side lengths a and b.
Rearrange the formula to make C the subject.
Use inverse operations to move a number, term, or variable.
As \frac{1}{2}ab\sin(C) can be written as \frac{ab\sin(C)}{2}, we can cancel the denominator by multiplying both sides of the formula by 2.
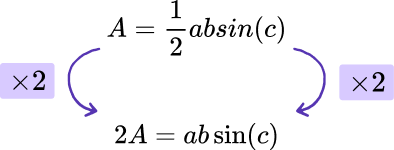
Repeat this process until the remaining variable is the subject.
As ab\sin(C) can be written as ab\times\sin(C) we can divide the right hand side of the formula by ab. Doing the same process to the left side of the equals sign, we have
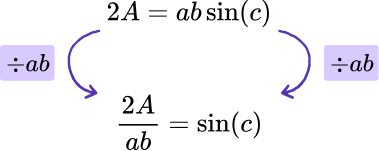
Currently the sine of C is being calculated and so we need to use the inverse sine function on both sides of the equation to leave us with C as the subject.
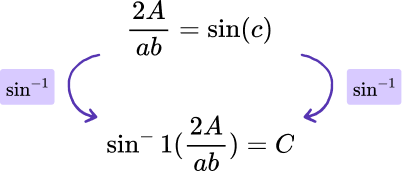
Example 6: sine rule
The sine rule states that the ratio of a side length, divided by the sine of the opposing angle is the same for all three sides of a triangle. This is expressed as
\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}.Using the relationship between the two side lengths a and b only, make B the subject of the formula
\frac{a}{\sin(A)}=\frac{b}{\sin(B)}.Use inverse operations to move a number, term, or variable.
Currently \sin(B) is on the denominator of a fraction, and so we need to multiply both sides of the formula by \sin(B) so it is no longer a divisor.
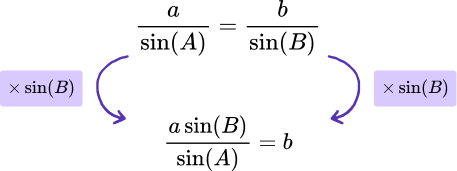
Repeat this process until the remaining variable is the subject.
We then need to divide both sides by a,
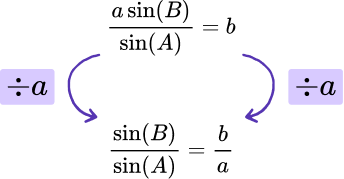
and multiply both sides by \sin(A).
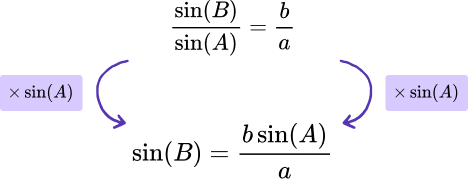
Calculating the inverse sine of both sides of the equation, gives us the solution.
B = \sin^{-1}\left(\cfrac{b\sin(A)}{a}\right)
Common misconceptions
- Removing the quantity from a fraction incorrectly
When a quantity is contained within the numerator of a fraction, we need to multiply both sides of the formula by the denominator of the fraction so that the numerator is “free” from the division. We can then continue to rearrange the formula.
For example, make x the subject of the formula
M=\frac{y-x}{2}.

- Incorrect inverse operation
The inverse operation used is incorrect. For example, let M=DV. Here, the formula is rearranged to get M-V=D and so the value of V has been subtracted, rather than divided. The correct answer should be \frac{M}{V}=D.
- Moving letters
Letters are simply moved from one side of the equals sign to the other. For example, A=lw becomes Al=w which is incorrect. Instead we need to use the inverse operation to multiplying by l, which is to divide both sides by l to get w=\frac{A}{l}.
- Not multiplying or dividing throughout
When given the equation y=mx+c, if we divided both sides of the equation by m we should get \frac{y}{m}=x+\frac{c}{m} whereas students would incorrectly write \frac{y}{m}=x+c. When multiplying and dividing by something, every term on each side of the equals sign must be multiplied or divided by it.
- Expanding brackets
When expanding brackets, all terms within the bracket must be multiplied by the value on the outside of the bracket. For example, expanding the brackets of 2(x+3), we get 2x+6 as both of the terms inside the bracket have been multiplied by 2.
- The power disappears
When we have a variable raised to a power, we must use inverse operations to remove that power. For example, if we have x^{4} we need to calculate the 4th root of the variable to get x. We cannot disregard the power, for example x^{4}=64 so x=64 is incorrect. The correct answer is x=4.
- Factorising to get one variable
The surface area of a cone is written as A=\pi{r^2}+\pi{rl}. If we wanted to make \pi the subject, students write \pi=\frac{A-\pi{r^2}}{rl} which has \pi occurring on both sides of the equation and therefore we need to know the value of \pi to calculate the value of \pi, which we cannot do.
Instead, we need to factorise the right hand side of the equation in terms of \pi so we get A=\pi(r^{2}+rl). Dividing both sides by r^{2}+rl we get \pi=\frac{A}{r^{2}+rl} which calculates the value of \pi given the total surface area of a cone (A), the radius of the base (r), and the slant length (l).
Practice changing the subject of a formula questions
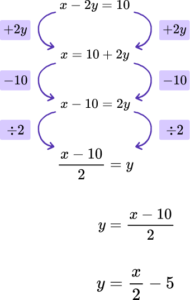
1. Rearrange x-2y=10 to make y the subject. Write your answer in the form y=\frac{x}{b}+c where b and c are integers.




2. Rearrange the iterative formula u_{n+1}=2u_{n}+3 to make u _n the subject.




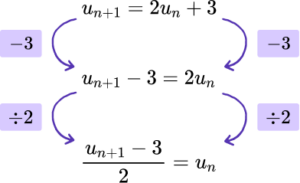
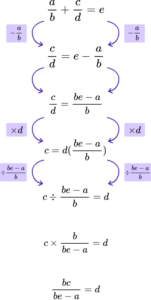
3. Given that \frac{a}{b}+\frac{c}{d}=e, make d the subject of the formula.
Write your solution as a simplified single fraction.




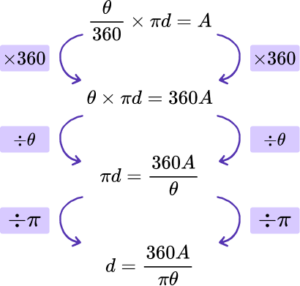
4. The formula \frac{\theta}{360}\times\pi{d}=A represents the arc length A of a sector of a circle with diameter d.
Make d the subject of the formula.




5. Make b the subject of the formula A=\frac{1}{2}ab\sin(C).




6. Make B the subject of the formula \frac{a}{\sin(A)}=\frac{b}{\sin(B)}.




\frac{a\sin \left( B \right)}{\sin \left( A \right)}=b
a\sin \left( B \right)=b\sin \left( A \right)
\sin \left( B \right)=\frac{b\sin \left( A \right)}{a}
B={{\sin }^{-1}}\left( \frac{b\sin \left( A \right)}{a} \right)
Changing the subject of a formula GCSE questions
1. If A and B are two different events, then
P(A \cup B)=P(A)+P(B)-P(A \cap B).Rearrange this formula to make P(A \cap B) the subject.
(2 marks)
(1)
P(A \cap B)=P(A)+P(B)-P(A \cup B)(1)
2. Percentage change is calculated using the formula,
P=\frac{y-x}{x} \times 100.
Where P is the percentage change,
x is the initial amount,
y is the new amount.
Given that C=y-x where C represents the change between the initial and the new amount, write a formula for C in terms of P and x.
(3 marks)
P=\frac{C}{x} \times 100 or equivalent.
(1)
Px=100C \ or \ \frac{P}{100}=\frac{C}{x}
(1)
C=\frac{Px}{100}(1)
3. The gradient of a line m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}. Rearrange the formula to make y_{2} the subject.
(2 marks)
(1)
m(x_{2}-x_{1})+y_{1}=y_{2}(1)
Learning checklist
You have now learned how to:
-
Understand and use inverse operations
-
Understand and use standard mathematical formulae
-
Rearrange formulae to change the subject
The next lessons are
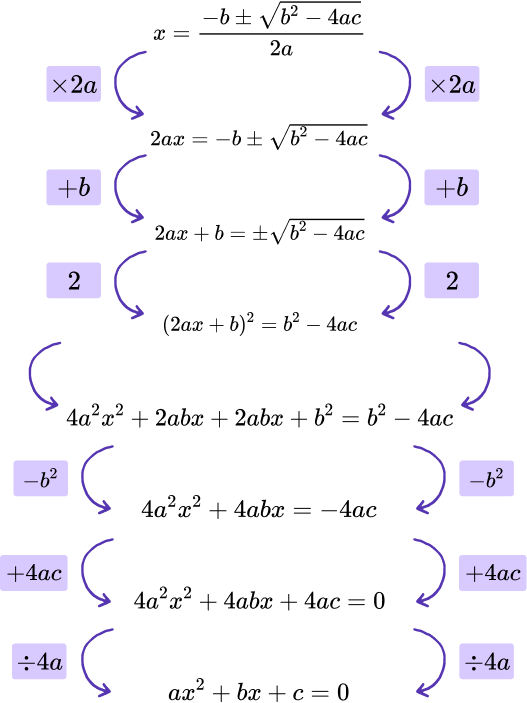
Rearrange the quadratic formula to the general form of a quadratic equation
For example,
Rearrange the quadratic formula
x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}to get the general form of a quadratic equation
ax^{2}+bx+c=0 .
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.