One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Expanding brackets Expand and simplify

Factors, multiples, powers and roots

Algebraic expressions

Adding and subtracting negative numbers

Multiplying and dividing negative numbers

Highest common factor (HCF)

Laws of indices Square numbers and square roots

This topic is relevant for:

GCSE Maths Algebra Factorising Single Bracket

Factorising Single Brackets

Here we will learn about factorising to single brackets by finding the highest common factor.

There are also factorising to single brackets worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

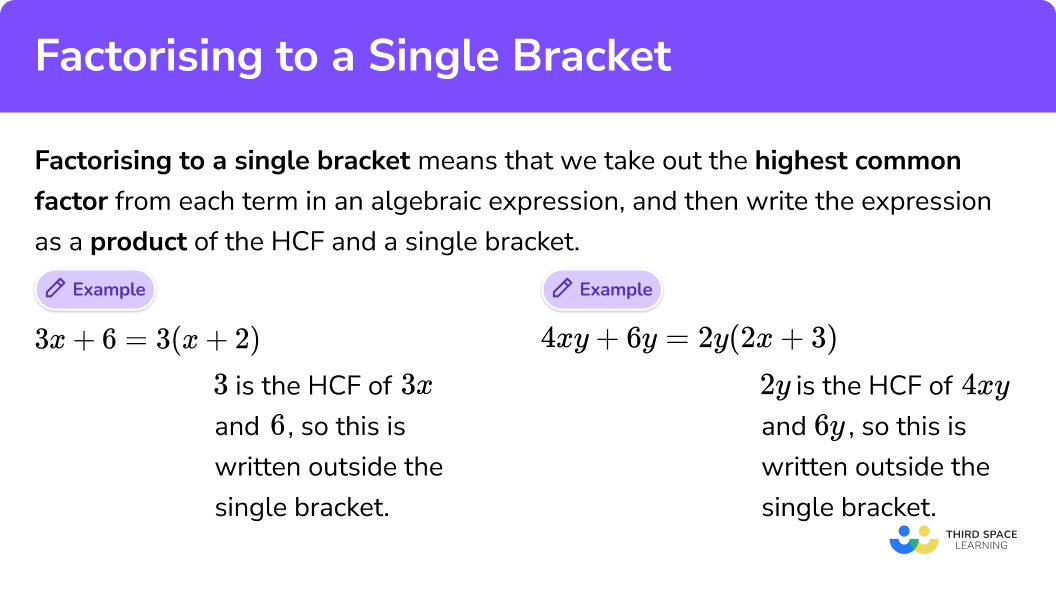
How to factorise into single brackets

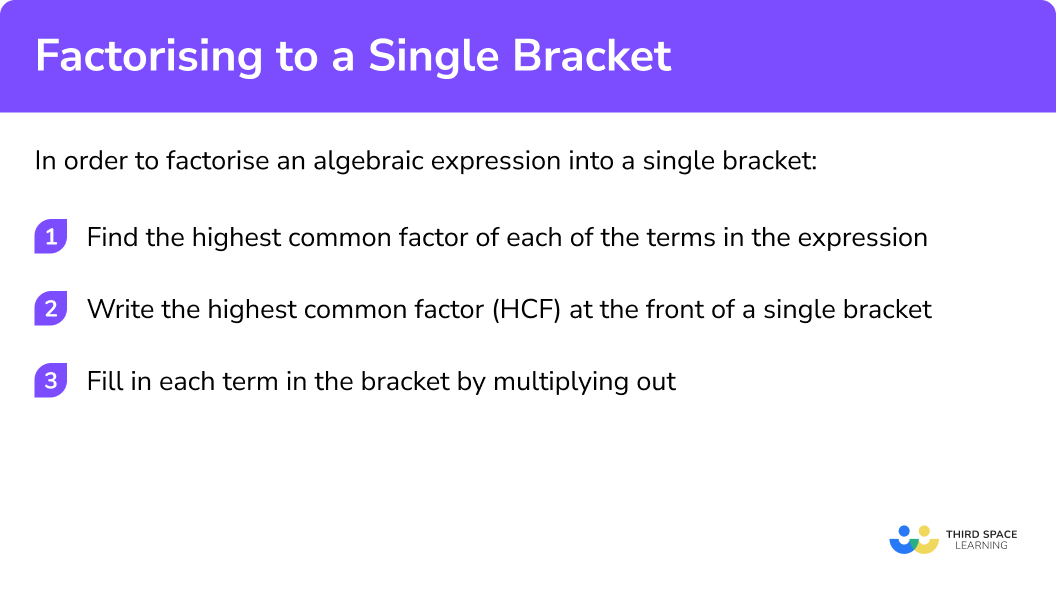
In order to factorise an algebraic expression into a single bracket:

Find the highest common factor of each of the terms in the expression.
Write the highest common factor (HCF) at the front of a single bracket
Fill in each term in the bracket by multiplying out.

Explain how to factorise into single brackets in 3 steps

We can factorise lots of different types of expressions into single brackets including some quadratics like x² + 5 or 3x² – 5x.

For quadratic expressions of the form x² + bx + c or ax² + bx + c we will need to factorise into double brackets – you can learn all about this in the factorising quadratics lesson.

Check out our main factorising lesson for a complete summary of all the different ways we can factorise expressions, and then explore our other factorising lessons for detailed step-by-step guides and worksheets on each type.

Factorising single brackets worksheet

Get your free factorising single brackets worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Factorising single brackets worksheet

Get your free factorising single brackets worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Factorising single brackets examples

Example 1: variable in just one term

Fully factorise:

\[\color{#00BC89}3x \color{#7C4DFF}{+6}\]

1Find the highest common factor (HCF) of the numbers 3 (the coefficient of x) and 6 (the constant).

Factors of 3:
1, 3

Factors of 6:
1, 6
2, 3

Top tip:
Writing the factor pairs makes it easier to list all the factors

The highest common factor (HCF) of 3x and 6 is 3

2Write the highest common factor (HCF) at the front of the single bracket.

\[\color{#FF9100}3(\qquad+\qquad)\]

3Fill in each term in the bracket by multiplying out.

What do I need to multiply 3 by to give me 3x?

\[\color{#FF9100}3\times \color{#62F030}x = \color{#00bc89}3x\]

What do I need to multiply 3 by to give me 6?

\[\color{#FF9100}3\times \color{#92009E}2 = \color{#7C4DFF}6\]

\[\color{#FF9100}3(\color{#62F030}x+\color{#92009E}2)\]

We can check the answer by multiplying out the bracket!

\[3(x+2)=3x+6\]

Example 2: variable in just one term

Fully factorise:

\[\color{#7C4DFF}{14}\color{#00BC89}{-7}y\]

Find the highest common factor (HCF) of the numbers 14 and 7.

Factors of 14:
1, 14
2, 7

Factors of 7:
1, 7

The highest common factor (HCF) of 14 and 7y is 7

Write the highest common factor (HCF) at the front of the single bracket.

\[\color{#FF9100}7(\qquad-\qquad)\]

Fill in each term in the bracket by multiplying out.

What do I need to multiply 7 by to give me 14?

\[\color{#FF9100}7\times \color{#62F030}2 = \color{#7C4DFF}{14}\]

What do I need to multiply 7 by to give me 7y?

\[\color{#FF9100}7\times \color{#92009E}y = \color{#00bc89}7y\]

\[\color{#FF9100}7(\color{#62F030}2-\color{#92009E}y)\]

(don’t forget to keep the – here)

We can check the answer by multiplying out the bracket!

\[7(2-y)=14-7y\]

Example 3: variable in two terms

Fully factorise:

\[\color{#FE47EC}8x^{2}\color{#00BC89}{+12}x\]

Find the highest common factor (HCF) of the numbers 8 and 12.

Factors of 8:
1, 8
2, 4

Factors of 12:
1, 12
2, 6
3, 4

Find the highest common factor (HCF) of the variables x² and x

x² = x ✕ x

x = x

The highest common factor (HCF) of 8x² and 12x is 4x

Write the highest common factor (HCF) at the front of the single bracket.

\[\color{#FF9100}{4x}(\qquad+\qquad)\]

Fill in each term in the bracket by multiplying out.

What do I need to multiply 4x by to give me 8x² ?

\[\color{#FF9100}{4x} \times \color{#62F030}{2x} = \color{#FE47EC}8x^2\]

What do I need to multiply 4x by give me 12x?

\[\color{#FF9100}{4x} \times \color{#92009E}3 = \color{#00BC89}{12}x\]

\[\color{#FF9100}{4x}(\color{#62F030}{2x} + \color{#92009E}3)\]

We can check the answer by multiplying out the bracket!

4x(2x + 3) = 8x² + 12x

Example 4: variable in two terms

Fully factorise:

\[\color{#FE47EC}{15}y^{2}\color{#0EE2EF}{-10}xy\]

Find the highest common factor (HCF) of the numbers 15 and 10.

Factors of 15:
1, 15
3, 5

Factors of 10:
1, 10
2, 5

Find the highest common factor (HCF) of the letters y² and xy

y² = y ✕ y

xy = x ✕ y

The highest common factor (HCF) of 15y² and 10xy is 5y

Write the highest common factor (HCF) at the front of the single bracket.

\[\color{#FF9100}{5y}(\qquad-\qquad)\]

Fill in each term in the bracket by multiplying out.

What do I need to multiply 5y by to give me 15y²?

\[\color{#FF9100}{5y} \times \color{#62F030}{3y} = \color{#FE47EC}{15}y^2\]

What do I need to multiply 5y by to give me 10xy?

\[\color{#FF9100}{5y} \times \color{#92009E}{2x} = \color{#0EE2EF}{10}xy\]

\[\color{#FF9100}{5y}(\color{#62F030}{3y}\color{#92009E}{-2x})\]

We can check the answer by multiplying out the bracket!

\[5y(3y-2x)=15y^{2}-10xy\]

Example 5: variable in two out of three terms

Fully factorise:

\[\color{#00BC89}{6}x \color{#00BC89}{+2}y \color{#7C4DFF}{- 12}\]

Find the highest common factor (HCF) of the numbers 6, 2 and 12

Factors of 6:
1, 6
2, 3

Factors of 2:
1, 2

Factors of 12:
1, 12
2, 6
3,4

The highest common factor (HCF) of 6 and 2 and 12 is 2

Write the highest common factor (HCF) at the front of the single bracket.

\[\color{#FF9100}2(\qquad+\qquad-\qquad)\]

Fill in each term in the bracket by multiplying out.

What do I need to multiply 2 by to give me 6x?

\[\color{#FF9100}2 \times \color{#62F030}{3x} = \color{#00bc89}6x\]

What do I need to multiply 2 by to give me 2y?

\[\color{#FF9100}2 \times \color{#92009E}y = \color{#00bc89}2y\]

What do I need to multiply 2 by to give me 12?

\[\color{#FF9100}2 \times \color{#F6C929}6 = \color{#7C4DFF}{12}\]

\[\color{#FF9100}2(\color{#62F030}{3x} \color{#92009E}{+y} \color{#F6C929}{-6})\]

Don’t forget to keep the – here!

We can check the answer by multiplying out the bracket!

\[2(3x+y-6)=6x+2y-12\]

Example 6: variable in two out of three terms

Fully factorise:

\[\color{#0EE2EF}{12}xy\color{#FE47EC}{-4}x^{2}y\color{#FE47EC}{+8}xy^{2}\]

Find the highest common factor (HCF) of the numbers 12, 4 and 8

Factors of 12:
1, 12
2, 6
3,4

Factors of 4:
1, 4
2, 2

Factors of 8:
1, 8
2, 4

Find the highest common factor (HCF) of the letters x² and x²y and xy²

xy = x ✕ y

x²y = x ✕ x ✕ y

xy² = x ✕ y ✕ y

The highest common factor (HCF) of 12x² and 4x²y and 8xy² is 4xy

Write the highest common factor (HCF) at the front of the single bracket.

\[\color{#FF9100}4xy(\qquad-\qquad+\qquad)\]

Fill in each term in the bracket by multiplying out.

What do I need to multiply 4xy by to give me 12xy?

\[\color{#FF9100}{4xy} \times \color{#62F030}3 = \color{#0EE2EF}{12}xy\]

What do I need to multiply 4xy by to give me 4x²y?

\[\color{#FF9100}{4xy} \times \color{#92009E}x = \color{#FE47EC}4x^2y\]

What do I need to multiply 4xy by to give me 8xy²?

\[\color{#FF9100}{4xy} \times \color{#F6C929}{2y} = \color{#FE47EC}8xy^2\]

\[\color{#FF9100}{4xy}( \color{#62F030}3\color{#92009E}{-x}\color{#F6C929}{+2y})\]

Don’t forget to keep the – here!

We can check the answer by multiplying out the bracket!

\[4xy(3-x+2y)=12xy-4x^{2}y+8xy^{2}\]

Common misconceptions

These are some of the common misconceptions around factorising into single brackets

We must fully factorise

12x² – 6x = 2(6x² – 3x)

Here we have factorised the expression, however it is not fully factorised because 2 is not the highest common factor.

6x is the highest common factor, so this is the correct final answer:

12x² – 6x = 6x(2x – 1)
12x² – 6x

Even though this a quadratic expression we still factorise it to give a single bracket because it is not in the form ax² + bx + c

Practice factorising single brackets questions

$5(x+10)$

$5x(x+2)$

$5(x+2)$

$x(5+10)$

The highest common factor of $5$ and $10$ is $5$ . We can divide each term in the original expression by $5$ , which means the bracket must contain $(x+2)$ .

2(4-y)

2(4+y)

2y(4-y)

8(1-2y)

The highest common factor of $8$ and $2$ is $2$ . We can divide each term in the original expression by $2$ ; the bracket must contain a minus sign just like the original expression.

$3x(6x-4)$

$6(3x^{2}-2x)$

$3(6x^{2}-4x)$

$6x(3x-2)$

The highest common factor of $18x^{2}$ and $12x$ is $6x$ . We can divide each term by $6x$ , which means the bracket must contain $(3x-2)$ .

$4y(5y-4x)$

$y(20y-16x)$

$2y(10y-8x)$

$4xy(5y-4x)$

The highest common factor of $20y^{2}$ and $16xy$ is $4y$ . We can divide each term by $4y$ , which means the bracket must contain $(5y-4x)$ .

$3xy(6-2y+5x)$

$3(6-2y+5x)$

$18(1-2y+5x)$

$3(6+2y+5x)$

The highest common factor of $18,6y$ and $15x$ is $3$ . We can divide each term by $3$ , which means the bracket must contain $(6-2y+5x)$ .

$12y(1-3x^{2}+2y)$

$3y(4+3x^{2}+2y)$

$3y(4-3x^{2}+2y)$

$3y(4-3x^{2}-2y)$

The highest common factor of $12y, 9x^{2}y$ and $6y^{2}$ is $3y$ . We can divide each term by $3y$ , which means the bracket must contain $(4-3x^{2}+2y)$ .

Factorising single brackets GCSE questions

1. Factorise: 5x-20

Show answer

5(x-4)

(1 mark)

2. Factorise fully: 8x² + 12xy

Show answer

4x(2x+3y)

(2 marks)

3. Factorise: x² + 8x

Show answer

x(x+8)

(1 mark)

Learning checklist

Manipulate algebraic expressions by taking out common factors to factorise into a single bracket
~~Factorise quadratic expressions of the form x² + bx + c~~
~~Factorise quadratic expressions of the form of the difference of two squares~~
~~Factorising quadratic expressions of the form ax² + bx + c (H)~~

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths revision programme.

What is factorising?

Factorising single brackets worksheet

How to factorise single brackets

Factorising single brackets examples

Common misconceptions

Factorising questions (single brackets)

Factorising GCSE questions (single brackets)

Learning checklist

Next lessons

Still stuck?

FREE GCSE Maths Scheme of Work Guide

An essential guide for all SLT and subject leaders looking to plan and build a new scheme of work, including how to decide what to teach and for how long

Explores tried and tested approaches and includes examples and templates you can use immediately in your school.

Download free

Factorising Single Brackets

How to factorise into single brackets

Explain how to factorise into single brackets in 3 steps

Related factorising lessons

Factorising single brackets worksheet

Factorising single brackets worksheet

Factorising single brackets examples

Example 1: variable in just one term

Example 2: variable in just one term

Example 3: variable in two terms

Example 4: variable in two terms

Example 5: variable in two out of three terms

Example 6: variable in two out of three terms

Common misconceptions

Practice factorising single brackets questions

Factorising single brackets GCSE questions

Learning checklist

The next lessons are

Still stuck?

FREE GCSE Maths Scheme of Work Guide