One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Expanding brackets Expand and simplify Factors and multiples Powers and roots Algebraic expressions Adding and subtracting negative numbers Multiplying and dividing negative numbers Highest common factor (HCF) Law of indices Square numbers and square rootsThis topic is relevant for:

Difference Of Two Squares
Here we will learn how to factorise using the difference of two squares method for a quadratic in the form
There are also difference of two squares questions and an extensive worksheet based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
Related factorising lessons
If you’re looking for a summary of all the different ways you can factorise expressions then you may find it helpful to start with our main factorising lesson or look in detail at the other lessons in this section.
What is the difference of two squares?
The difference of two squares is a method of factorising used when an algebraic expression includes two squared terms, one subtracted from the other:
When we are subtracting a squared term from another squared term we can use the difference of two squares method. Square numbers are sometimes called perfect squares.
An example of an expression we can factorise using the difference of two squares might be
To use quadratic factorisation on an expression in the form
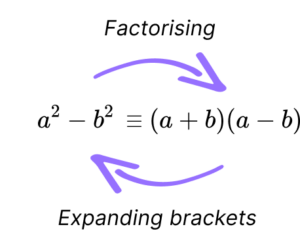
What is the difference of two squares?


Difference of two squares worksheet

Get your free difference of two squares worksheet with 20+ reasoning and applied questions, answers and mark scheme.
DOWNLOAD FREE
Difference of two squares worksheet

Get your free difference of two squares worksheet with 20+ reasoning and applied questions, answers and mark scheme.
DOWNLOAD FREEHow to factorise using difference of two squares
In order to factorise an algebraic expression using the difference of two squares:
- Write down two brackets.
- Square root the first term and write it on the left hand side of both brackets.
- Square root the last term and write it on the right hand side of both brackets.
- Put a + in the middle of one bracket and a – in the middle of the other (the order doesn’t matter.)
Explain how to factorise using the difference of two squares in 4 steps

Difference of two squares examples
Example 1: x2 variable has a coefficient of 1
Fully factorise
- Write down two brackets
2Square root the first term and write it on the left hand side of both brackets
3Square root the last term and write it on the right hand side of both brackets.
4Put a + in the middle of one bracket and a – in the middle of the other (the order doesn’t matter).
We can check the final answer by multiplying out the brackets!
Example 2: y2 variable has a coefficient of 1
Fully factorise
Write down two brackets
Square root the first term and write it on the left hand side of both brackets
Square root the last term and write it on the right hand side of both brackets
Put a + in the middle of one bracket and a – in the middle of the other (the order doesn’t matter.)
We can check the final answer by multiplying out the brackets!
Example 3: x2 variable has a coefficient greater than 1
Fully factorise
Write down two brackets
Square root the first term and write it on the left hand side of both brackets
Square root the last term and write it on the right hand side of both brackets
Put a + in the middle of one bracket and a – in the middle of the other (the order doesn’t matter.
We can check the final answer by multiplying out the brackets!
Example 4: coefficient of both terms is greater than 1
Fully factorise
Write down two brackets
Square root the first term and write it on the left hand side of both brackets
Square root the last term and write it on the right hand side of both brackets
Put a + in the middle of one bracket and a – in the middle of the other (the order doesn’t matter.)
We can check the final answer by multiplying out the brackets!
Example 5: combining HCF / GCF and difference of two squares
Fully factorise
Be careful, this one is not the difference of two squares!
We first need to find the highest or greatest common factor (
Write down two brackets with the x at the front
Square root the first term and write it on the left hand side of both brackets
Square root the last term and write it on the right hand side of both brackets
Put a + in the middle of one bracket and a – in the middle of the other (the order doesn’t matter.)
We can check the final answer by multiplying out the brackets!
Common misconceptions
- The order of subtraction
There must simply be a + in one bracket, and a – in the other, the order doesn’t matter.
- Square root the entire term
Remember to square root the entire term including the coefficients of the variables.
E.g.
- Terms used can vary
The term factorising can sometimes be written as ‘factoring’ or factorization’
Practice difference of two squares questions
1. Fully factorise:
x^{2}-25




Recognising the expression as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{x^{2}}&=x\\ \sqrt{25}&=5\\ \end{aligned}
and then rewrite as a product of two brackets
(x+5)(x-5)
2. Fully factorise:
y^{2}-81




Recognising the expression as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{y^{2}}&=y\\ \sqrt{81}&=9\\ \end{aligned}
and then rewrite as a product of two brackets
(y+9)(y-9)
3. Fully factorise:
49-y^{2}




Recognising the expression as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{49}&=7\\ \sqrt{y^{2}}&=y\\ \end{aligned}
and then rewrite as a product of two brackets
(7+y)(7-y)
4. Fully factorise:
4-x^{2}




Recognising the expression as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{4}&=2\\ \sqrt{x^{2}}&=x\\ \end{aligned}
and then rewrite as a product of two brackets
(2+x)(2-x)
5. Factorise:
16x^{2}-100




First, we can factor 4 out of each term.
This gives 4(4x^{2}-25)
Recognising the expression in the brackets as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{4x^{2}}&=2x\\ \sqrt{25}&=5\\ \end{aligned}
and then rewrite as a product of two brackets muliplied by the 4.
4(2x+5)(2x-5)6. Fully factorise:
49-9y^{2}




Recognising the expression as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{49}&=7\\ \sqrt{9y^{2}}&=3y\\ \end{aligned}
and then rewrite as a product of two brackets
(7+3y)(7-3y)
7. Factorise:
81x^{2}-16y^{2}




Recognising the expression as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{81x^{2}}&=9x\\ \sqrt{16y^{2}}&=4y\\ \end{aligned}
and then rewrite as a product of two brackets
(9x+4y)(9x-4y)
8. Fully factorise:
4x^{3}-36x




The first thing we need to do is divide by the highest common factor of the two terms and rewrite the expression
4x^{3}-36x=4x(x^{2}-9)
Recognising the expression in the bracket as a difference of two squares means we can square root each term
\begin{aligned} \sqrt{x^{2}}&=x\\ \sqrt{9}&=3\\ \end{aligned}
and then rewrite as a product of two brackets. Don’t forget to also multiply by the factor we initially divided by
4x(x+3)(x-3)
Difference of two squares GCSE questions
1. Factorise: x2 – 100
= (x + 10)(x – 10)
(1 mark)
2. Factorise: y2 – 49
= (y + 7)(y – 7)
(1 mark)
3. Factorise: 2x2 – 50
= 2(x2 – 25) = 2(x + 5)(x – 5)
(2 marks)
Learning checklist
You have now learnt how to:
- Manipulate algebraic expressions by taking out common factors to factorise into a single bracket
- Factorise quadratic expressions of the form x^{2}+ bx + c
- Factorise quadratic expressions of the form of the difference of two squares
- Factorising quadratic expressions of the form ax^{2} + bx + c (H)
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.