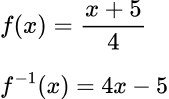One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

GCSE Maths Topics

Geometry - Maths GCSE Number - Maths GCSE Probability - Maths GCSE Ratio and proportion - Maths GCSE Statistics - Maths GCSE

This topic is relevant for:

GCSE Maths Algebra

Algebra

Algebra – Maths GCSE

Here we will learn about algebra, including algebraic expressions, equations, functions, sequences and types of graphs.

There are also algebra worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is algebra?

Algebra is an area of mathematics which deals with variables which can be expressed using symbols or letters.

In this page we will link to lots of other pages that will help with a variety of algebra topics.

Here are the different areas of algebra that may be examined in GCSE mathematics.

What is algebra?

Algebraic expressions

An algebraic expression is a set of terms with letters and numbers that are combined using addition $(+),$ subtraction $(-),$ multiplication $(\times)$ and division $(\div).$

A term is an individual letter or number.

A variable is a letter or symbol whose quantity can change.

A constant is a fixed value like a number.

A coefficient is a numerical quantity placed before a variable.

For example,

$3x+2,\,4w-5y$ or $6{{m}^{2}}-7h+\frac{4}{k}$

Step-by-step guide: Algebraic expressions

There are many different tasks you may be asked to perform with an algebraic expression.

Simplifying expressions

We can simplify algebraic expressions by expanding brackets collecting like terms.

For example,

Expand and simplify $2(x-3y)+4(3x+2y)$ .

\begin{aligned} 2\left( x-3y \right)+4\left( 3x+2y \right)&\equiv 2x-6y+12x+8y \\\\ & \equiv 14x+2y \end{aligned}

We can also simplify algebraic fractions.

For example,

\begin{aligned} \frac{3}{x}+\frac{1}{2 y} &=\frac{3(2 y)+x}{2 x y} \\\\ &=\frac{6 y+x}{2 x y} \end{aligned}

Step-by-step guide: Simplifying expressions

Substitution

For example,

Find the value of $6m-4g,$ when $m=5$ and $g=-3$ .

\begin{aligned} 6 m-4 g &=6(5)-4(-3) \\\\ &=30-(-12) \\\\ &=42 \end{aligned}

Step-by-step guide: Substitution

Factorising

For example,

Factorise fully $16{{a}^{3}}b-28a{{b}^{2}}$ .

16{{a}^{3}}b-28a{{b}^{2}}\equiv 4ab\left( 4{{a}^{2}}-7b \right)

Step-by-step guide: Factorising

Algebra worksheet

Get your free algebra worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Algebra worksheet

Get your free algebra worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Algebraic equations

Equations are mathematical expressions which contain a variable and an equals sign.

For example,

3 x-7=24

2 a-3 b=12

\frac{5 x-2}{4}=2 x+1

Step-by-step guide: Equations

There are many different tasks you may be asked to perform with equations.

Solving equations

For example,

Solve to find $x.$

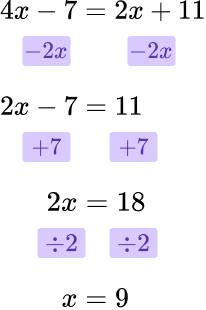
To solve quadratic equations we may need to use the quadratic formula.

Step-by-step guide: Solving equations

Rearranging equations

For example,

Rearrange the formula to make $p$ the subject.

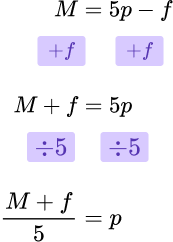
Step-by-step guide: Rearranging equations

Simultaneous equations

For example,

Find the values of $x$ and $y$ if

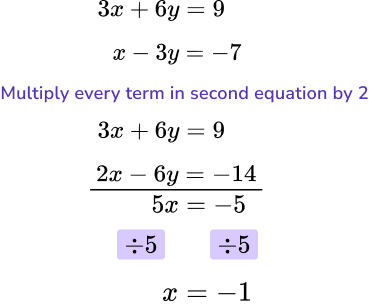
Substitute $x=-1$ into either of the original equations.

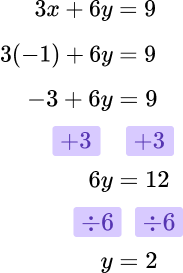
Clearly state the final answer.

Step-by-step guide: Simultaneous equations

Laws of indices

An index is a small number that tells us how many times a term has been multiplied by itself.

The plural of index is indices.

$2 \times 2 \times 2$ can be written as $2^3$ , where $2$ is the base and $3$ is the index.

You can simplify expressions using laws of indices.

For example, simplify $\frac{{{x}^{3}}\times \ {{x}^{7}}}{{{x}^{4}}}$ .

\begin{aligned} \frac{{{x}^{3}}\times {{x}^{7}}}{{{x}^{4}}} & =\frac{{{x}^{10}}}{{{x}^{4}}} \\\\ & ={{x}^{6}} \end{aligned}

Laws of indices provide us with rules for simplifying calculations or expressions involving powers of the same base. This means that the larger number or letter must be the same.


Multiplying	To multiply two powers with the same base, add the indices.	$x^{a}\times{x^{b}}=x^{a+b}$
Dividing	To divide two powers with the same base, subtract the indices.	$x^{a}\div{x^{b}}=x^{a-b}$
Brackets	To raise one power to another power, multiply the indices.	$(x^{a})^{b}=x^{ab}$
Fraction	To raise a base to a fraction $\frac{m}{n}$ , calculate the $nth$ root of the base, raised to the power $m.$	$x^{\frac{m}{n}}=\sqrt[n]{x^m}$
Negative	To raise a base to a negative number, take the positive power of the reciprocal.	$x^{-a}=\frac{1}{x^a}$

Step-by-step guide: Laws of indices

Types of graphs

Types of graphs include different types of straight and curved graphs.

We need to be able to recognise and distinguish between the main types of graphs and understand the algebraic expressions for them.

Here are some of the types of graphs you will need to be able to recognise and sketch.

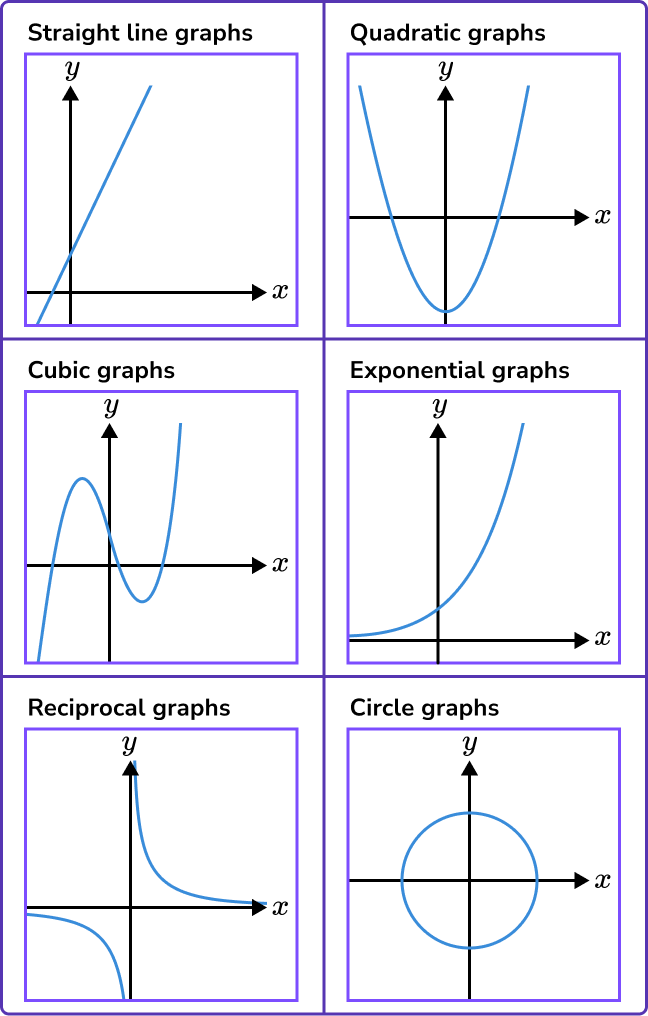
Step-by-step guide: Types of graph

Inequalities

Inequalities compare numbers or expressions in order of size.

There are four ways we can compare terms.

Less than

For example,

x \ < \ 2

$‘x$ is less than $2.’$

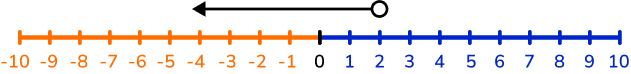
Algebra - Maths GCSE inequalities image 1

Greater than

For example,

x \ > \ 2

$‘x$ is greater than $2.’$

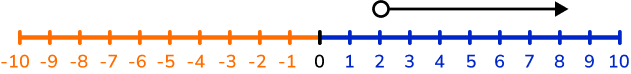
Algebra - Maths GCSE inequalities image 2

Less than or equal to

For example,

x \ \leq \ 2

$‘x$ is less than or equal to $2.’$

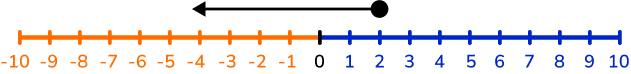
Algebra - Maths GCSE inequalities image 3

Greater than or equal to

For example,

x \ \geq \ 2

$‘x$ is greater than or equal to $2.’$

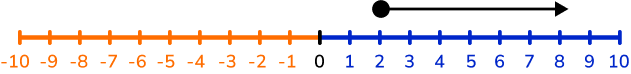
Algebra - Maths GCSE inequalities image 4

We can use inequalities in a variety of different ways.

Inequalities on a number line
List integer values in a solution set
Solving inequalities
Quadratic inequalities

Step-by-step guide: Inequalities

Sequences

A number sequence is a set of numbers that follow a particular pattern or rule to get from term to term.

There are four main types of sequences you need to know, they are arithmetic sequences, geometric sequences, quadratic sequences and special sequences.

Step-by-step guide: Sequences

Arithmetic sequences

An arithmetic sequence is an ordered set of numbers that have a common difference between each term.

If we add or subtract the same number each time to make the sequence, it is an arithmetic sequence.

Step-by-step guide: Arithmetic sequences

Geometric sequences

A geometric sequence is an ordered set of numbers that progresses by multiplying or dividing each term by a common ratio.

If we multiply or divide by the same number each time to make the sequence, it is a geometric sequence.

Step-by-step guide: Geometric sequences (coming soon)

Quadratic sequences

A quadratic sequence is an ordered set of numbers that follow a rule based on the sequence $n^{2}=1, 4, 9, 16, 25, ...$ (the square numbers).

The difference between each term is not equal, but the second difference is.

Step-by-step guide: Quadratic sequences

Special sequences

You will need to be able to recognise some important special sequences.

The Fibonacci Sequence is a famous sequence. We generate the Fibonacci Sequence by adding the previous two terms together to work out the next term.

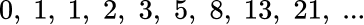
Functions in algebra

Functions in algebra are used to describe the operation being applied to an input in order to get an output.

Step-by-step guide: Functions in algebra

Function machines

Functions can be presented using a function machine.

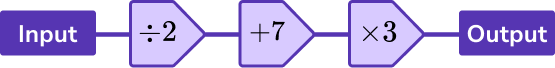
Algebra - Maths GCSE functions in algebra image 1

Step-by-step guide: Function machines

Function notation

Functions can be described using function notation.

The $f$ in $f(x)$ is known as the function that is being applied to a variable $x.$ Other letters such as $g$ and $h$ are also commonly used.

For example,

Let’s look at a function $f$ described by a function machine.

Algebra - Maths GCSE functions in algebra image 2

Then let’s rewrite this using function notation.

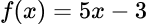
Algebra - Maths GCSE functions in algebra image 3

Step-by-step guide: Function notation

Composite functions

We can combine functions to make composite functions.

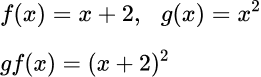
Algebra - Maths GCSE functions in algebra image 4

Step-by-step guide: Composite functions

Inverse functions

We can also find inverse functions.

Algebra - Maths GCSE functions in algebra image 5

Step-by-step guide: Inverse functions

Common misconceptions

The sign in front of the term

The sign in front of the term is part of the term. When we underline the like terms, we must include the sign in front of the term.

Using exponents (powers)

In order for two terms to be ‘like terms’ they need the same combination of variables.

$3x^2$ and $5x^2$ are like terms.

$2a^{2}b$ and $-5a^{2}b$ are like terms.

BUT

$3x^2$ and $5x$ are not like terms.

$2a^{2}b$ and $-5ab$ are not like terms.

Solutions to equations are not always positive whole numbers

Solutions to equations can be positive integers (whole numbers), but they can also be negative. They can also be decimals or fractions.

Writing solutions as an inequality

When solving an inequality, a common error is to not include the inequality sign in the solution.

For example,

$x + 5 < 8$ .

The solution is $x < 3.$

$x = 3$ or $‘3’$ are not acceptable as it does not identify the range of values that satisfy the inequality.

Mistaking composite functions for the product of the functions

A common mistake is to think that $fg(x)$ means $f(x) \times g(x).$

For example,

If $f(x)=x+1$ and $g(x)=2x-3,$ the error will be to think that $fg(x)=(x+1)(2x-3),$ rather than the correct answer of $fg(x)=2x-2.$

When a power is outside the bracket you must raise all terms inside the bracket by that power

For example, when we simplify $(4a)^{2}$ we must remember to square both the $4$ and the $a.$ It is common to forget to square the $4.$

$(4 a)^{2}=4 a \times 4 a=4^{2} a^{2}=16 a^{2}$

The brackets mean the entire term is squared.

Practice algebra questions

2y+7

-2y+7

-2y-47

-2y+47

The expression expands to give $4y-20-6y+27$ .

99

7

39

-9

5(3)-4(-6)=15+24=39

3.5

6

-3.5

-6

5x-3x=8-20

2x=-12

x=-6

y=-2x+3

y=2x+3

y=-2x-3

y=2x-3

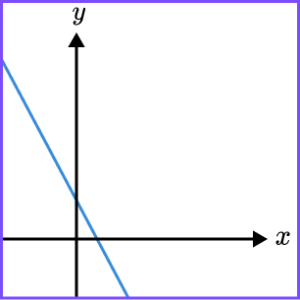
The straight line graph has a negative gradient and a positive $y$ -intercept.

2{{a}^{4}}{{b}^{12}}

16{{a}^{4}}{{b}^{7}}

16{{a}^{4}}{{b}^{12}}

2a{{b}^{7}}

\begin{aligned} (2a{{b}^{3}})^{4} &= 2ab^3\times 2ab^3\times 2ab^3\times 2ab^3 \\\\ &= 2^4 a^4 (b^3)^4 \\\\ &=16a^4 b^{12} \end{aligned}

9

15

8

10

gf\left( 2 \right)={{\left( 2\left( 2 \right)-1 \right)}^{2}}+1=10

Algebra GCSE questions

1. Here are the first $4$ terms of an arithmetic sequence.

-2, 5, 12, 19, \dots.

(a) Find the $nth$ term of the sequence.

(b) Find the $100th$ term of the sequence.

(4 marks)

Show answer

(a)

7n

(1)

Correct constant term of $-9$ .

(1)

(b)

Attempt to use $nth$ term $7(100)-9$ .

(1)

691

(1)

2. (a) Factorise fully.

36{{x}^{4}}{{y}^{3}}-27x{{y}^{2}}

(b) Solve to find $x.$

6x-2=14-2x

(4 marks)

Show answer

(a)

A correctly factorised expression but not fully factorised. For example, $3x\left( 12{{x}^{3}}{{y}^{3}}-9{{y}^{2}} \right)$ .

(1)

Answer of $9x{{y}^{2}}\left( 4{{x}^{3}}y-3 \right)$ .

(1)

(b)

Method to isolate the $x.$ For example, $8x=16$ .

(1)

x=2

(1)

3. Draw lines to match the graph with the correct equation.

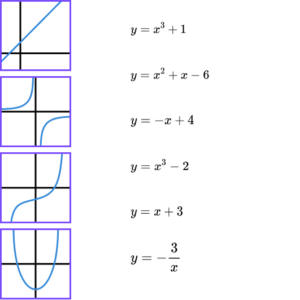
Algebra - Maths GCSE gcse question 3 image 1

(4 marks)

Show answer

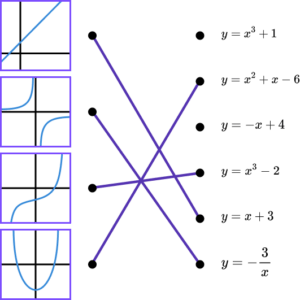
Algebra - Maths GCSE gcse question 3 image 2

$1$ correct

(1)

$2$ correct

(1)

$3$ correct

(1)

$4$ correct

(1)

The most popular lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.