24 Fraction Questions For Year 6 (SATs): Complete With Answers

April 15, 2024 | 7 min read

Emma Johnson

Here are 24 free fractions questions for Year 6, a perfect resource to use with pupils in the run up to the KS2 Maths SATs in May. In addition to the questions, we’ve also included useful background information on the fractions knowledge Year 6 pupils need to acquire by the end of KS2. This includes the key vocabulary, concepts and fraction knowledge from earlier Key Stage 2 year groups.

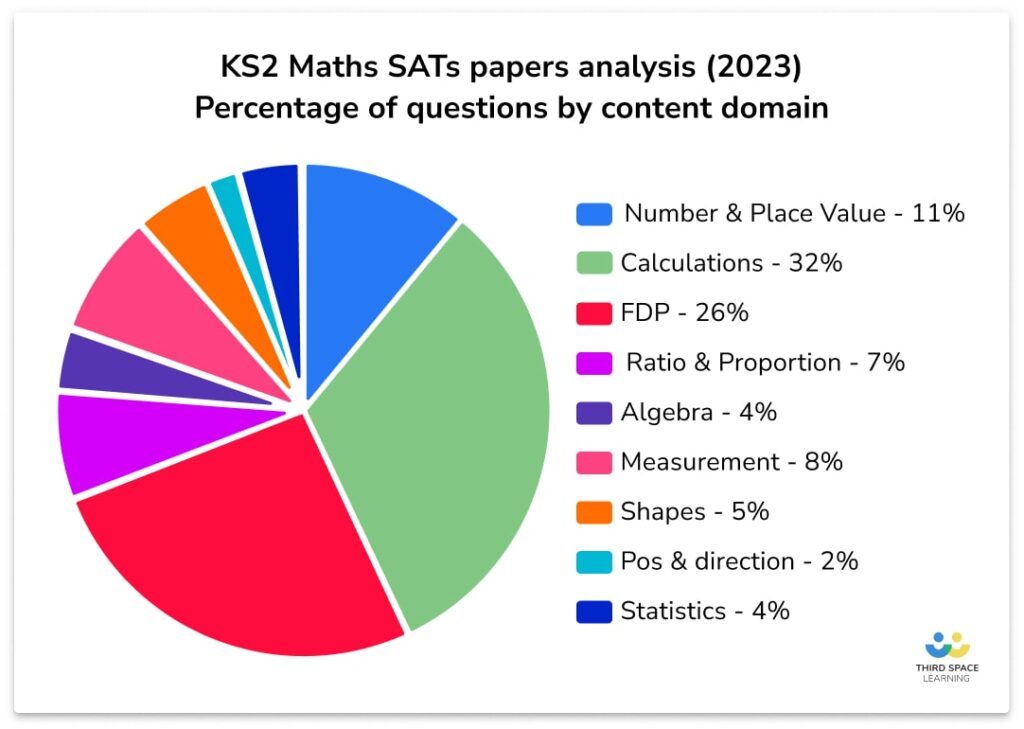
We’re focusing on fractions here as they are a key component of the National Curriculum and a topic pupils are guaranteed to see multiple times in the end of Key Stage 2 SATS.

Alongside decimals and percentages, fractions make up the third highest content domain across the arithmetic and reasoning papers.

SATs 2023 question breakdown of all 3 papers

This article is one of a series providing teachers with a bank of hundreds of SATs questions for Year 6 that they can continue to refer back to through the year.

What do Year 6 pupils need to know about fractions?

Throughout Key Stage 2, pupils cover a substantial amount of work on fractions. In Year 6, pupils continue to build on this knowledge from previous years, helping them to become proficient in the end of KS2 fractions standards.

National Curriculum expectations for fractions in KS2 maths:

In Year 3 pupils learn to:

Recognise unit and non-unit fractions
Identify equivalent fractions
Order and compare fractions
Add and subtract fractions with the same denominator

In Year 4 pupils learn to:

Build on their understanding of equivalent fractions
Continue adding and subtracting fractions with the same denominator
Count in tenths and hundredths

In Year 5 pupils learn to:

Compare and order fractions with different denominators
Add and subtract fractions with different denominators
Convert between improper fractions and mixed numbers
Begin to multiply fractions and mixed numbers
Explore relationships between equivalent fractions, decimals and percentages

By the time students reach Year 6, the expectation is that students will have a secure understanding of fractions.

Considerable exposure to concrete resources and visual images should ensure they have a good conceptual understanding of fractions.

In Year 6 pupils learn to:

Build on knowledge developed throughout KS2
Be confident adding subtracting, multiplying and dividing fractions and simplifying their final answer
Calculate equivalent fractions, decimals and percentages

200 arithmetic and reasoning questions for Year 6

Download 100 free arithmetic questions and 100 free reasoning questions for Year 6. Includes answers and mark scheme.

Download Free Now!

Thousands of pupils develop their fractions knowledge and understanding every week through our one to one online maths lessons. Our maths experts have developed hundreds of fraction questions for pupils to work through step by step with their tutor to build confidence. Try the one to one maths fraction lessons for yourself in this free downloadable SATs intervention pack.

What fractions questions appear in the KS2 SATs?

Predominantly, the KS2 SATs arithmetic paper consists of fluency style fraction questions. Reasoning Paper 2 and Paper 3 are made up of more word problem style questions.

Children can expect to answer questions on the four operations and fractions. Often, these question types increase in levels of difficulty throughout the paper.

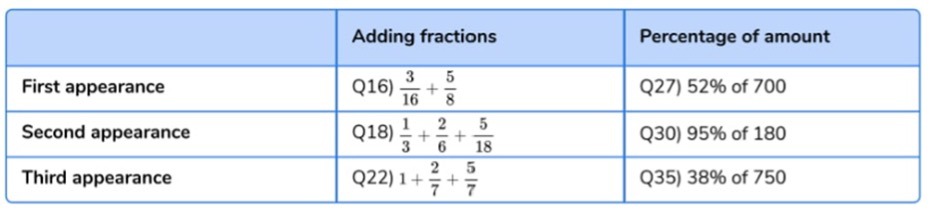
For example, in the 2023 arithmetic paper, children were given three adding fractions questions. The first question required pupils to add fractions within 1 while the second question asked Year 6 pupils to add 3 fractions within 1. The third fractions question required pupils to add 3 fractions with a total greater than 1.

Fractions question difficult in the 2023 KS2 SATs

Fractions questions included in this article cover simple fractions questions and become increasingly harder.

Questions begin with fluency skills and progress to questions involving reasoning and problem solving.

Key Year 6 fractions terminology needed for these questions

Pupils should have a strong understanding of key fractions terminology by the time they reach Year 6.

Here are some of the key terms children should have a secure understanding of:

Denominator: The bottom number of a fraction. This tells us how many equal parts make up a whole.
Numerator: The top number of a fraction. This tells us how many equal parts of the whole are being considered.
Unit fraction: A fraction with a numerator of 1.
Non-unit fraction: A fraction with a numerator greater than 1.
Whole number: An integer, that isn’t a fraction or a decimal. Whole numbers can be expressed as a fraction by placing the whole number in place of the numerator and a 1 in place of the denominator.
Decimal: Another representation of a fraction. The digits to the left of the decimal point represent the whole number and the digits after the decimal point indicate the fraction of the whole number. For example, 2.14
Improper fractions: Fractions with a numerator greater than the denominator. These fractions have a total value of more than one whole.
For example, $\frac{13}{4}$
Mixed numbers: A combination of a whole number and a fraction. When a number is greater than one whole, it can be written as either an improper fraction or a mixed number.
For example, 1 $\frac{2}{3}$ = $\frac{5}{3}$
Equivalent fractions: Fractions that represent the same value but have a different numerator and denominator.
For example, $\frac{3}{4}$ = $\frac{9}{12}$
Multiples and factors: These refer to the common divisors and multiples of the numerator and denominator.
Highest common factor (HCF) is the largest number that the numerator and denominator can be divided by.
For example, $\frac{6}{12}$ both 6 and 12 can be divided by 6
Lowest common multiple (LCM) is the smallest number that both numbers are factors of.
For example, $\frac{2}{4}$ both 2 and 4 are factors of 4
Common denominator: The shared multiple of the denominators of two or more fractions.
For example, $\frac{3}{4}$ and $\frac{2}{6}$ share a common denominator of 12
Simplify fractions: When fractions are reduced to their lowest and simplest form.
For example, $\frac{4}{20}$ can be simplified to $\frac{1}{5}$

24 fractions questions for Year 6

Fraction questions for Year 6: comparing and ordering

Fraction question 1

Compare the following pairs of fractions and put the > , < or = symbol between each pair:

$\frac{5}{8}$ $\frac{3}{4}$

$\frac{2}{3}$ $\frac{5}{12}$

$\frac{7}{10}$ $\frac{3}{5}$

Answer:

$\frac{5}{8}$ < $\frac{3}{4}$

$\frac{2}{3}$ > $\frac{5}{12}$

$\frac{7}{10}$ > $\frac{3}{5}$

$\frac{3}{4}$ = $\frac{6}{8}$

$\frac{2}{3}$ = $\frac{8}{12}$

$\frac{3}{5}$ = $\frac{6}{10}$

Fraction question 2

Order the following fractions from smallest to biggest:

$\frac{2}{5}$ $\frac{2}{3}$ $\frac{2}{6}$ $\frac{2}{4}$ $\frac{2}{10}$

Answer: $\frac{2}{10}$ $\frac{2}{6}$ $\frac{2}{5}$ $\frac{2}{4}$ $\frac{2}{3}$

Fraction question 3

Re-arrange the following fractions from greatest to smallest

$\frac{4}{6}$ $\frac{1}{3}$ $\frac{7}{12}$

Answer: $\frac{4}{6}$ $\frac{7}{12}$ $\frac{1}{3}$

$\frac{4}{6}$ = $\frac{8}{12}$

$\frac{1}{3}$ = $\frac{4}{12}$

$\frac{7}{12}$ = $\frac{7}{12}$

Fraction question 4

Hamza ate $\frac{3}{5}$ of his bag of 50 sweets, Jack ate $\frac{4}{10}$ of his bag of 50 sweets. Who ate the most sweets:

Answer: Hamza

$\frac{3}{5}$ = $\frac{6}{10}$

$\frac{6}{10}$ is greater than $\frac{4}{10}$

Fraction question 5

Sophie, Ben and Alice were taking part in a running competition. With 10 minutes to go, Sophie had completed $\frac{4}{5}$ of the route, Ben had completed katex]\frac{5}{6}[/katex] and Alice had completed $\frac{2}{3}$ . Order them from 1-3, with the person who had run the most at the top.

Answer: 1st: Ben, 2nd: Sophie, 3rd: Alice

Sophie $\frac{4}{5}$ = 2 $\frac{24}{30}$

Ben $\frac{5}{6}$ = $\frac{25}{30}$

Alice $\frac{2}{3}$ = $\frac{20}{30}$

Fraction question 6

Chloe, Ahmed and Mason have each ordered a pizza. Chloe ate $\frac{3}{8}$ of her pizza, Ahmed ate $\frac{5}{12}$ of his and Mason ate $\frac{2}{6}$ . Who ate the most pizza? Order them from 1 to 3.

Answer: Ahmed at the most, followed by Chloe, then Mason ate the least.

Chloe: $\frac{3}{8}$ = $\frac{9}{24}$

Ahmed: $\frac{5}{12}$ = $\frac{10}{24}$

Mason: $\frac{2}{6}$ = $\frac{8}{24}$

Fraction questions for Year 6: four operations with fractions

Fraction question 7

$\frac{3}{8}$ + $\frac{2}{4}$ =

Answer: $\frac{7}{8}$

$\frac{3}{8}$ + $\frac{4}{8}$ = $\frac{7}{8}$

Fraction question 8

$\frac{9}{12}$ – $\frac{1}{3}$ =

Answer: $\frac{5}{12}$

$\frac{9}{12}$ – $\frac{4}{12}$ = $\frac{5}{12}$

Fraction question 9

$\frac{3}{5}$ x 7 =

Answer: 4 $\frac{1}{5}$

$\frac{3}{5}$ x 7 = $\frac{21}{5}$ = 4 $\frac{1}{5}$

Fraction question 10

$\frac{12}{17}$ ÷ 3 =

Answer: $\frac{4}{17}$

Fraction question 11

$\frac{7}{12}$ ÷ 4 =

Answer: $\frac{7}{48}$

$\frac{7}{12}$ ÷ 4 = $\frac{1}{4}$ of $\frac{7}{12}$

$\frac{1}{4}$ x $\frac{7}{12}$ = $\frac{7}{48}$

Fraction question 12

Masie, Chloe and Jess are sharing some pizzas. Maisie eats $\frac{5}{8}$ of a pizza, Chloe eats $\frac{3}{8}$ and Jess eats $\frac{6}{8}$ . How much pizza have they eaten altogether?

Answer: 1 $\frac{6}{8}$ or 1 $\frac{3}{4}$

$\frac{5}{8}$ + $\frac{3}{8}$ + $\frac{6}{8}$ = $\frac{14}{8}$ = 1 $\frac{6}{8}$

Fraction question 13

4 friends have 3 $\frac{1}{5}$ pizzas to share between them. If they share it equally, how much pizza will each of the friends receive?

Answer: $\frac{4}{5}$ of a pizza

3 $\frac{1}{5}$ = $\frac{16}{5}$

$\frac{16}{5}$ ÷ 4 = $\frac{4}{5}$

Fraction question 14

Adam is baking some cooking. He needs $\frac{3}{4}$ of a cup of sugar to make 10 cookies. If he wants to bake 60 cookies, how many cups of sugar will he need?

Answer: 4 $\frac{1}{2}$ cups

$\frac{3}{4}$ x 6 = $\frac{18}{4}$ = 4 $\frac{2}{4}$ = 4 $\frac{1}{2}$

Fraction questions for Year 6: fractions, decimals and percentages

Fraction question 15

Order the following from smallest to largest:

35%, 0.3, $\frac{34}{100}$

Answer: 0.3, $\frac{34}{100}$ , 35%

35% = $\frac{35}{100}$

0.3 = $\frac{30}{100}$

\frac{34}{100}

Fraction question 16

Circle three numbers which add up to 1:

0.5 15% $\frac{1}{4}$ 10% 0.2 $\frac{7}{10}$

Answer: $\frac{7}{10}$ 0.2 10%

\frac{7}{10}

0.2 = $\frac{2}{10}$

10% = $\frac{1}{10}$

Fraction question 17

Which of the following are equivalent to 20%?

0.02 $\frac{40}{200}$ $\frac{10}{50}$ 0.2 $\frac{2}{10}$ 0.22 $\frac{40}{100}$ $\frac{2}{5}$

Answer: $\frac{40}{200}$ $\frac{10}{50}$ 0.2 $\frac{2}{10}$

Fraction question 18

What is 35% of 240?

Answer: 84

10% = 24

5% = 12

30% = 72

35% = 84

Fraction question 19

Sam, Amy and Lucy have raised £560 in a sponsored swim.

Sam raised $\frac{3}{8}$ of the total

Amy raised 30% of the total.

How much did Lucy raise?

Answer: £182

Sam: $\frac{3}{8}$ of 560 = £210

Amy: 30% of 560 = £168

£210 + £168 = £378

Lucy raised £560 – £378 = £182

Fraction question 20

There are 60 sweets in a bag. The sweets are red, orange or yellow.

$\frac{5}{12}$ of the sweets are red

40% are orange.

How many are yellow?

Answer: 11 yellow sweets

$\frac{5}{12}$ of 60 = 25

40% of 60 = 24

15 + 24 = 49

60 – 49 = 11

Fraction questions for Year 6: fraction word problems

Fraction question 21

Max has 150 pages in his book. He has read $\frac{3}{5}$ of the book. How many pages does he have left to read?

Answer: 60 pages left to read.

$\frac{1}{5}$ of 150 = 30

$\frac{2}{5}$ of 150 = 60

Fraction question 22

Sienna has half of a pizza left. She cuts the half a pizza into 4 equal sized pieces. What fraction is each piece?

Answer: $\frac{1}{8}$

$\frac{1}{2}$ ÷ 4 = $\frac{1}{8}$

Fraction question 23

8 friends share some pizzas equally. Each person is given $\frac{5}{8}$ of a pizza. How much pizza did the eat altogether?

Answer: 5 pizzas

$\frac{5}{8}$ x 8 = $\frac{40}{8}$ = 5

Fraction question 24

Oliver had some birthday money to buy some clothes. He spent $\frac{1}{5}$ of the money on a T-shirt, $\frac{1}{4}$ on a hoodie and $\frac{1}{2}$ on jeans. If he spent £12.50 on the hoodie, how much did he have left after his shopping trip?

Answer: £2.50

$\frac{1}{4}$ = £12.50

Total = £50

$\frac{1}{5}$ = £10

$\frac{1}{2}$ = £25

Total spent = £12.50 + £10 + £25 = £47.50

£50 – £47.50 = £2.50

FAQs

How do you teach fractions in KS2?

Fractions are a very abstract concept, which many children can find difficult. The best way to teach fractions is through the use of manipulatives and visual images, such as fraction circles, fraction cubes, fraction walls and number lines. Once children are secure using the practical and visual aids, they can progress to more abstract work. Children should also work to ensure they are confident with the times tables, which will make life easier when working on more challenging fractions questions.

What is the easiest way to teach fractions?

Children should be introduced to fractions through the use of concrete resources, such as fraction cubes and circles. These can be used for a whole range of topics including, equivalent fractions and to add, subtract, multiply, divide, order and compare fractions. Once secure, children can use visual images to continue to focus on the conceptual understanding, before moving on to more abstract work.

How to do fractions for Year 6?

Children should be secure in fluency style questions, using both concrete resources and visual images, before progressing onto more abstract work, reasoning, and problem solving questions in different contexts.

Are fractions important in daily life?

Fractions are an essential skill required throughout day to day life. Securing the fundamental concepts of fractions, decimals and percentages in Year 6 allows pupils to tackle more challenging concepts when learning more difficult fractions for GCSE and beyond. Use these 24 fraction questions for KS2 to GCSE to help prepare pupils when they encounter fractions in real life.

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.