One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Fractions, decimals and percentages Adding and subtracting fractions Bar chartsThis topic is relevant for:

Relative Frequency
Here we will learn about relative frequency, including how to calculate it.
There are also relative frequency worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is relative frequency?
Relative frequency is the number of times an event happens divided by the total number of outcomes that took place in an experiment, known as the number of trials.
To calculate the relative frequency we can use the formula,
\text{Relative frequency = }\frac{\text{frequency of event occurring}}{\text{total number of trials of the experiment}}For example,

Jo made a four-sided spinner out of a piece of card and a pencil. She spun the spinner 50 times and the spinner landed on a three 15 times. Calculate the relative frequency of the spinner landing on a three.
Relative frequency of landing on a three = \frac{15}{50} or \frac{3}{10} or 0.3 or 30\%.
The more times an experiment is carried out, the more reliable the relative frequency will be and closer to the theoretical probability.
What is relative frequency?

How to calculate relative frequency
In order to calculate relative frequency:
- Find the number of times the event occurs.
- Find the number of trials of the experiment.
- Use the formula
\textbf{Relative frequency = }\frac{\textbf{frequency of event occurring}}{\textbf{total number of trials of the experiment}}
Write your answer as a fraction, decimal or percentage.
Explain how to calculate relative frequency

Relative frequency worksheet

Get your free relative frequency worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Relative frequency worksheet

Get your free relative frequency worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on probability distribution
Relative frequency is part of our series of lessons to support revision on probability distribution. You may find it helpful to start with the main probability distribution lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Relative frequency examples
Example 1: calculating relative frequency
A coin is flipped 50 times and shows heads on 22 occasions. Calculate the relative frequency of the coin showing heads.
- Find the number of times the event occurs.
The coin showed heads 22 times.
2Find the number of trials of the experiment.
The coin was flipped 50 times.
3Use the formula
\textbf{Relative frequency = }\frac{\textbf{frequency of event occurring}}{\textbf{total number of trials of the experiment}}
Write your answer as a fraction, decimal or percentage.
Relative frequency =\frac{22}{50}=0.44
Example 2: calculating relative frequency
A coin shows heads 15 times having been flipped 40 times. Calculate the relative frequency of the coin showing tails.
Find the number of times the event occurs.
If the coin showed heads 15 times, it would have showed tails 25 times.
Find the number of trials of the experiment.
The coin was flipped 40 times.
Use the formula
\textbf{Relative frequency = }\frac{\textbf{frequency of event occurring}}{\textbf{total number of trials of the experiment}}
Write your answer as a fraction, decimal or percentage.
Relative frequency =\frac{25}{40}=0.625
Example 3: calculating the number of trials if relative frequency is known
An experiment rolling a normal 6 -sided dice obtained the number 4 on 32 occasions.
The relative frequency of rolling a 4 was calculated as 0.2. Find the number of times the dice was rolled.
Find the number of times the event occurs.
The number 4 was rolled 32 times.
Find the number of trials of the experiment.
This is what we need to calculate using step 3.
Use the formula
\textbf{Relative frequency = }\frac{\textbf{frequency of event occurring}}{\textbf{total number of trials of the experiment}}
As we already know the relative frequency, substitute this and the frequency of rolling a 4 into the formula.
0.2=\frac{32}{\text{number of times the die was rolled}}
Rearrange the formula.
Number of times the dice was rolled =\frac{32}{0.2}=160 .
Common misconceptions
- Assuming relative frequency is equal to the theoretical probability
The relative frequency of an event is determined by the number of trials or observations. If an experiment only has a small number of trials it is possible for the relative frequency to be very different from the theoretical probability of the same event. For example – if a coin is flipped only 5 times, it is very possible for it to show heads on all 5 occasions.
- Assuming a relative frequency with few trials is a good estimate for the theoretical probability
The more times an experiment is carried out, the more reliable the relative frequency will be and closer to the theoretical probability.
Practice relative frequency questions
1. A coin is flipped 80 times and shows heads 50 times. Find the relative frequency for the coin showing heads, giving your answer as a fraction in its simplest form.




\frac{50}{80} simplifies to \frac{5}{8} .
2. A coin is flipped 60 times and shows tails 24 times. Find the relative frequency for the coin showing tails, giving your answer as a decimal.




3. A coin is flipped 50 times and shows heads 31 times. Find the relative frequency for the coin showing tails, giving your answer as a fraction.




If the coin shows heads 31 times it must show tails 19 times. 50-31 = 19.
4. A 3 sided spinner, numbered 1, \ 2 and 3, is spun 200 times. It lands on 1, \ 60 times, and lands on 2, \ 85 times. Calculate the relative frequency of the spinner landing on 3. Give your answer as a fraction in its simplest form.




\frac{55}{200}=\frac{11}{40}
5. A normal 6- sided dice is rolled 150 times. The relative frequency of the die landing on 2 is 0.36. How many times did the die land on 2?




6. A 4- sided spinner numbered 1 to 4 is spun n times in an experiment. The spinner lands on 3, 76 times. The relative frequency of the spinner landing on 3 was calculated as \frac{19}{75}. Find the value of n.




Relative frequency GCSE questions
1. A school recorded the number of times different fruits were bought by students for their lunch.

Find the relative frequency of
(a) a student buying an apple.
(b) a student not buying grapes.
(4 marks)
(a)
Evidence of a fraction with denominator 150 .
(1)
\frac{53}{150} or 0.353… or equivalent.
(1)
(b)
Evidence of a fraction with denominator 150 .
(1)
\frac{121}{150} or 0.8066… or equivalent.
(1)
2. Jenny is doing an experiment to test the fairness of a 6- sided dice. She rolled the dice 12 times and got the following results.
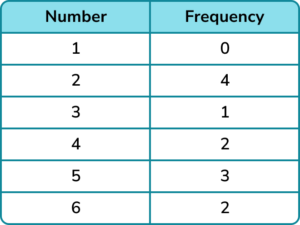
Jenny claims that the dice is not fair based on her results.
(a) Explain why Jenny may not be correct.
Simon repeats the experiment with the same die but rolls the die 36 times. His results are below.
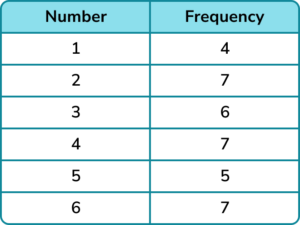
(b) Using all the information available find the relative frequency of rolling a 4 on the dice.
(4 marks)
(a)
“Jenny has not rolled the die many times” or “if she rolled the die more times her results would be more accurate”
(1)
(b)
7 + 2 = 9
(1)
12 + 36 = 48(1)
\frac{9}{48} or 0.1875 or equivalent.
(1)
3. A coin is flipped 500 times and shows tails 324 times.
Find the relative frequency of the coin showing heads.
(2 marks)
(1)
0.352 or equivalent.
(1)
Learning checklist
You have now learned how to:
- Calculate the relative frequency of an event occurring from a probability experiment
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.