GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Linear equations Rearranging equations Expanding brackets Negative numbersThis topic is relevant for:

Linear Inequalities
Here we will learn about linear inequalities, including what linear inequalities are and how to solve them.
There are also linear inequalities worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are linear inequalities?
Linear inequalities are inequalities where the power of the unknown in any algebraic expression is no higher than 1.
For example,
4x+1<13 which is read ‘4x+1 is less than 13’.
We can solve linear inequalities in the same way that we solve linear equations, by using inverse operations to isolate the variable.
The difference is that the answer will be a range of solutions rather than a single value.

The solution is x<3. This means that x is any value less than 3.
Notice that the inequality symbol remains the same throughout the working and for the answer.
The solution is x is less than 3. This means x could be any value less than 3 (for example, 2, \ 1.5, \ 1, \ 0, \ -1, \ -1000, etc.).
What are linear inequalities?

Negative numbers and inequalities
If you multiply or divide the inequality by a negative number, the direction of the inequality reverses.
For example, to solve the inequality -3x<30 we could divide both sides by -3.
Since multiplying or dividing by a negative reverses the direction of the inequality, this gives x>-10.
This only happens when we multiply or divide an inequality by a negative value.
How to solve linear inequalities
In order to solve linear inequalities:
- Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
- Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
- Write your solution with the inequality symbol.
Explain how to solve linear inequalities


Solving inequalities worksheet (includes linear inequalities)

Get your free linear inequalities worksheet of 20+ solving inequalities questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Solving inequalities worksheet (includes linear inequalities)

Get your free linear inequalities worksheet of 20+ solving inequalities questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on inequalities
Linear inequalities is part of our series of lessons to support revision on inequalities. You may find it helpful to start with the main inequalities lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Linear inequalities examples
Example 1: one step linear inequality
Solve the inequality x-7>10.
- Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
In this case you are adding ‘7’ to both sides.
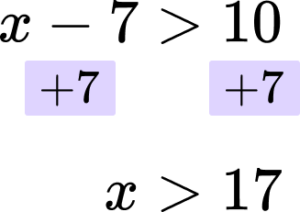
2Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case ‘x’ is already isolated.
3Write your solution with the inequality symbol.
In this example, we already have the solution, x>17.
Example 2: two step linear inequality
Solve the inequality 5x+4\le 19.
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
In this case you are subtracting ‘4’ from both sides.
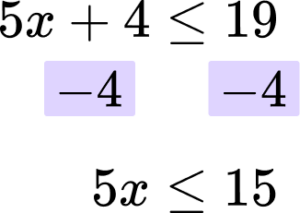
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you need to divide both sides by 5.
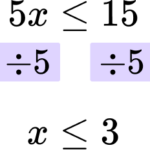
Write your solution with the inequality symbol.
The solution is x\le 3.
Note that multiplying or dividing by a positive number has no effect on the inequality sign itself.
Example 3: two step linear inequality with a fraction
Solve the inequality \frac{m}{3}+10<12.
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
In this case you are subtracting ‘10’ from both sides.
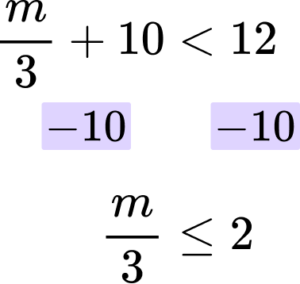
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case the coefficient of x is \frac{1}{3}. So you divide both sides by \frac{1}{3}.
Or you can think of it as multiplying both sides by 3.
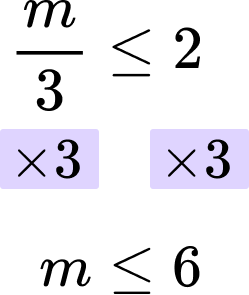
Write your solution with the inequality symbol.
The solution is m\le 6.
Example 4: linear inequality with negative coefficient
Solve the inequality 20-3x<8.
Note: There are two ways to deal with negative inequalities. The first is to move the negative to the other side in order to make it positive. The second is to divide by the negative. Dividing by a negative reverses the direction of the inequality sign.
Let’s look at both ways of dealing with this.
Moving the negative to the other side
Step 1: Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
In this case you are adding ‘3x’ to both sides.
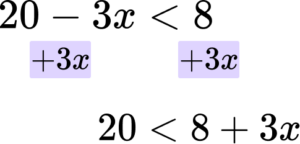
Then you are subtracting ‘8’ from both sides.
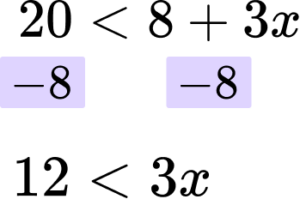
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you are dividing both sides by 3.
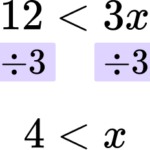
Write your solution with the inequality symbol.
The solution is 4<x.
Which can be written as x>4.
Dividing by a negative
Step 1: Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
In this case you are subtracting ‘20’ from both sides.
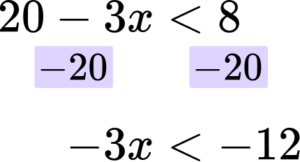
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you are dividing both sides by -3.
But you need to remember that dividing by a negative reverses the direction of the inequality.
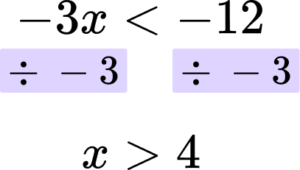
Write your solution with the inequality symbol.
The solution is x>4.
Both methods give the same solution, x>4.
Example 5: compound inequality
Solve the inequality -3<4x+1\le 17.
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
This inequality compares three expressions. Any operation we do must be applied to all three expressions.
In this case you are subtracting 1 from all three parts of the inequality.
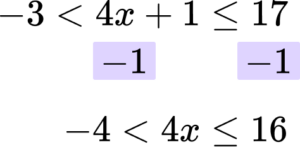
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you are dividing all three parts of the inequality by 4.
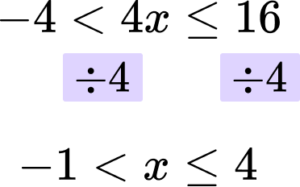
Write your solution with the inequality symbol.
The solution is -1<x\le 4.
Example 6: linear inequality with brackets
Solve the inequality 6(y-3)\le 42.
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
Before we can move the terms here we need to expand the brackets.
6(y-3)=6y-18 so we now have,
6y-18\le 42.
Then you are adding 18 to both sides.
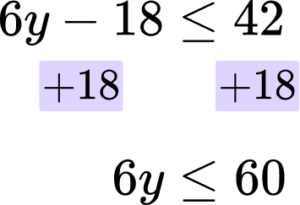
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you are dividing both sides by 6.
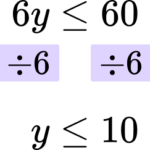
Write your solution with the inequality symbol.
The solution is y\le 10.
Example 7: linear inequality with unknowns on both sides
Solve the inequality 5t+7>9t-13.
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
It is always easiest to move the term involving the smaller number of the variable. In this case 5t is smaller than 9t so you are subtracting ‘5t’ from both sides.
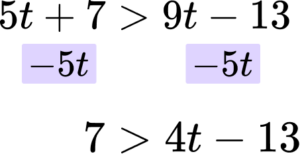
In this case the next step would be to add 13 to both sides.
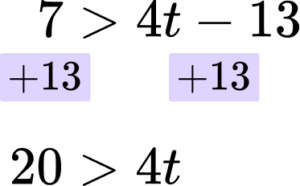
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you are dividing both sides by 4.
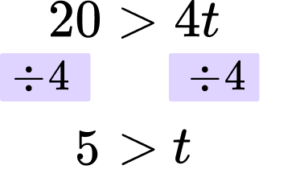
Write your solution with the inequality symbol.
The solution is 5>t which could also be written as t<5.
Example 8: linear inequality with brackets and unknowns on both sides
Solve the inequality 2(p+4)<6(4-p).
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
Before you can rearrange the inequality, you need to expand the brackets.
\begin{aligned} 2(p+4) &< 6(4-p) \\\\ 2p+8 &< 24-6p \end{aligned}
It is always easiest to move the term involving the smaller number of the variable. In this case -6p is smaller than 2p so you are adding 6p to both sides.
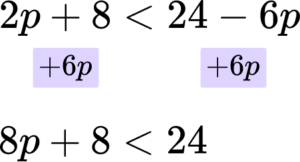
Then you are subtracting 8 from both sides.
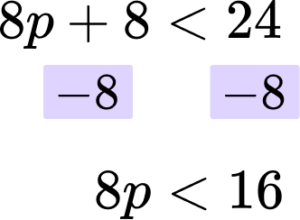
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you are dividing both sides by 8.
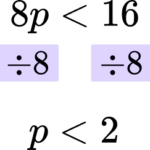
Write your solution with the inequality symbol.
The solution is p<2.
Common misconceptions
- Dropping the inequality
When solving inequalities students may use the same method as solving equations. During this process the inequality sign may be mixed up with the equality sign (=). It is important to ensure that the correct sign is used.
- Using the wrong operation
When working with equations and inequalities you need to remember to use the inverse operation.
For example, to solve x+8<14, you need to subtract 8 from both sides not add 8 to both sides.
- Performing the operation to the wrong side
Make sure you perform the operation to the correct side of an inequality.
For example, to solve \frac{x}{3}\ge12, multiplying by 3 gives x\ge 36, not 3x\ge 12.
Practice linear inequalities questions
1. Solve the inequality 5x<30.




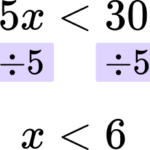
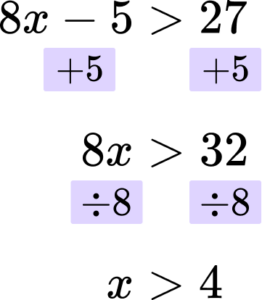
2. Solve the inequality 8x-5>27.




3. Solve the inequality \frac{x}{6}+2\ge 5.




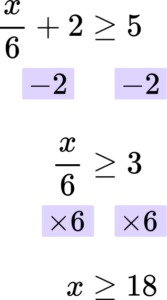
4. Solve the inequality 30-3x\le 27.




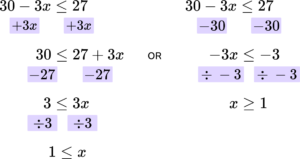
5. Solve the inequality 13<5x-2\le 38.




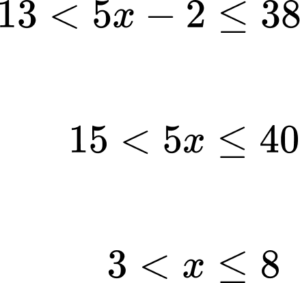
6. Solve the inequality 2(3x-1)<46.




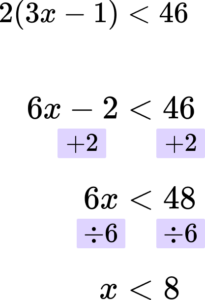
7. Solve the inequality 8x-2>5x+4.




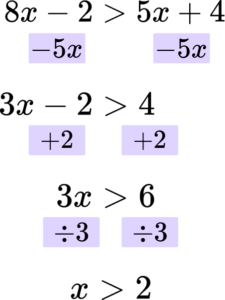
8. Solve the inequality 2(3x-2)\le 14(4-x).




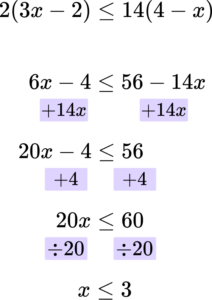
Linear inequalities GCSE questions
1. Solve the following inequality 3(4y+1)<63.
(2 marks)
(1)
12y<60
y<5
(1)
2. (a) Solve the inequality 2x+5\ge3.
(b) Represent the solution set on the number line below.
![]()
(3 marks)
(a)
2x \ge -2
(1)
x \ge -1(1)
(b)
![]()
Correct diagram with closed circle.
(1)
3. n is an integer such that 5<2n+1\le 13.
Write down all the possible values of n.
(3 marks)
(1)
2<n\le6(1)
n could be 3, \ 4, \ 5, \ 6.
(1)
Learning checklist
You have now learned how to:
-
Solve linear inequalities including ones with brackets and unknowns on both sides
-
Solve three-part linear inequalities
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.