GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Arithmetic Decimal places Factors and multiples Fractions Converting fractions, decimals and percentages Simplifying fractions Adding and subtracting fractions Scale mathsThis topic is relevant for:

Ratio
Here we will learn about ratio, including simplifying ratios, dividing a ratio into a quantity, ratios to fractions, and problem solving with ratios.
There are also ratio worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is ratio?
Ratio is a relationship between two or more quantities showing the number of times one is contained within the other(s).
Ratios are written in the form a:b , which is said “ a \ to \ b ” where a and b are normally integers, fractions or decimals.
They can also be represented in the form \frac{a}{b} (a fraction).
The order of the quantities in the ratio is important.
E.g.
If there are 10 boys in a class and 15 girls, we can say that the ratio of boys to girls is 10:15 which we say as “ 10 to 15 ”.
Ratios are used in real life very frequently.
We use ratios to bake cakes, convert currencies when you go on holiday, determine the shutter speed on a camera, draw scale models of buildings, calculate the speed of a car, determine the aspect ratio of television screens, read maps and many many more!
In the GCSE mathematics curriculum, topics that use ratios include the above as well as trigonometry, calculating the gradient of a line, measuring density or pressure of an object, calculating best value for money, speed calculations, and even within sampling techniques.
See also: 15 Ratio questions
What is ratio?

How to use ratios
We can use a variety of methods when interpreting ratios:
Working out ratio
A ratio can be written as a part to part and a part to whole.
We explore how to write a relationship as a ratio, manipulate ratios and real life ratio problems
E.g.
30 people attend a fitness class. 23 are female and the rest are male.
Write the part to part ratio of males to females.
Solution 7:23
Step-by-step guide: How to work out ratio
Simplifying ratios
Writing a ratio in its simplest form allows us to carry out calculations with ratios that are easier mathematically as the numbers we use are smaller.
We explore how to simplify a ratio, equivalent ratios and more real life ratio problems.
E.g.
Simplify fully the ratio 14:21:35 .
Solution 2:3:5
Step-by-step guide: Simplifying ratios
Dividing ratios
Dividing a quantity into a ratio can help us find how much the value of one or each part of a ratio is worth.
We explore how to divide a quantity into a ratio and use this to solve real life problems.
E.g.
Divide £50 into the ratio of 2:3 .
Solution £20:£30
Step-by-step guide: Dividing ratios
Ratio to fraction
When we express a ratio as a fraction, we need to know either the value of each part of the ratio or the total amount and the value of all but one part of the ratio (of which we need to find).
We explore using ratios to find fractions, and using fractions to find ratios.
E.g.
The ratio of red to blue counters is 3:4 . What fraction of the counters are blue?
Solution \frac{4}{7}
Step-by-step guide: Ratio to fraction
Ratio to percentage
Writing a ratio as fractions can be extended to then writing it as percentages.
E.g.
The ratio of green counters to yellow counters is 1:3. What percentage of the counters are yellow?
Solution: \frac{3}{4}=75%. 75% of the counters are yellow.
Step-by-step guide: Ratio to percentage
Ratio problem solving
Comprehension and a wide range of subject knowledge is required to solve problems involving ratios.
We explore how to set up and solve problems involving ratios.
E.g.
Jenny is x years old and Suzie is four times as old as Jenny. If the difference between their ages is 15 , how old is each person? Write your answer as a ratio of Jenny’s age to Suzie’s age.
Solution 5:20
Step-by-step guide: Ratio problem solving
Ratio scale
E.g.
Square A has an area of 9cm^2 . Square B has a perimeter of 20cm . Write the ratio of their side lengths in the form 1:n
Solution 1:\frac{5}{3}
Step-by-step guide: Ratio scale
Ratio worksheet

Get your free ratio worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Ratio worksheet

Get your free ratio worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEWrite as a ratio
Questions may ask you to write a situation as a ratio.
For example, a class has 12 boys and 17 girls, write the number of boys and the number of girls as a ratio. The answer would be 12:17.
Use a ratio
You may be given a ratio and asked to use the ratio to solve problems.
For example, a purple paint in made by mixing red and blue paint in the ratio 2:3. Use the ratio to work out how many litres of red and blue paint are needed to make 40 litres of purple paint.
Red:Blue=2:3 which has 5 parts in total. The total is the amount of purple paint.
We need to scale up the ratio so that there are 40 litres of purple paint by multiplying each part by 8.
Therefore there will be 16 litres of red paint and 24 litres of blue paint needed to make 40 litres of purple paint.
n:1 form
You may be asked to express a ratio in the form “n:1” or “1:n”. This would involve scaling the ratio so that one of the parts is 1.
For example,
Express the ratio 12:4 is the ratio of n:1. This would mean we have to scale the four so that it becomes 1. We can do this by dividing both parts of the ratio by 4 to become 3:1, with n= 3.
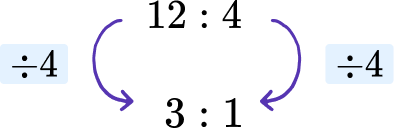
Ratio on a line
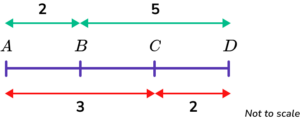
Some ratio problems involve points on a straight line and the ratios of the lengths of the different sections.
For example,The points A, B, C and D lie in order on a straight line.
AB:BD=2:5 and AC:CD=3:2

Then we add the ratio parts.
The total for the ratio parts needs to be the same, so we scale up using the lowest common multiple.
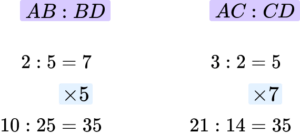
If we write the new ratios onto the line, we can then see what the different sections of the line are.
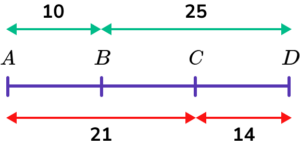
The sections BC will be 21-10=11.
Or alternatively BC can be calculated by 25-14=11.
The final answer is
AB:BC:CD=10:11:14
Ratio to graph
Ratio problems may also involve coordinates.
For example,
Points A and B have the coordinates (1,1) and (11,6) respectively.
Point C lies on the line AB such that AC:CB=3:2
Find point C.
The ratio 3:2 has 5 parts. We need to split the line AB into 5 equal parts. AC will be \frac{3}{5} of the line and CB will be \frac{2}{5} of the line.
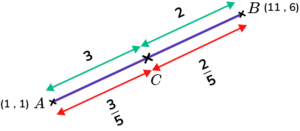
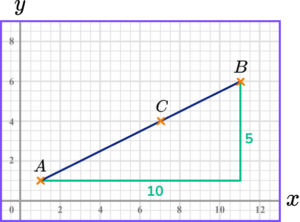
We can do this by looking at the x-coordinates and the y-coordinates separately.
The distance in the x direction is 11 - 1 = 10
So the x-coordinate will be 1 + \frac{3}{5} ✕ 10 = 7
The distance in the y direction is 6 - 1 = 5
So the x-coordinate will be 1 + \frac{3}{5} ✕ 5 = 4
So point C is at (7,4).
Ratio examples
Example 1: how to work out a ratio
The ratio of people who prefer skiing holidays to beach holidays is expressed as a bar model. State the ratio of people who prefer skiing holidays to the total number of people.
- State the number of shares in the required part of the ratio.
The Beach has 3 parts.
2State the number of shares in the other part(s) as required.
The total number of parts is 1+3=4
3Write the ratio using a colon : (and simplify when necessary).
3:4Example 2: simplifying ratios
Use a bar model to simplify the ratio 12:6
Representing the ratio 12:6 as a bar model, we have
Where purple represents 12 shares, and yellow represents 6 shares.
HCF(12,6)=6
As the highest common factor is 6 , we divide the bar above into six bars containing the same amount of purple shares, and yellow shares.
Each bar is the ratio 2:1 .
Solution: 2:1
Example 3: dividing ratios
Shirley wants to make shortbread for a party. The recipe requires flour, butter and sugar in the ratio 3:2:1 .
Shirley has 610g of flour, 450g of butter, and 750g of sugar.
Does she have enough of each ingredient to make 1.2kg of shortbread?
The weight of each ingredient in a shortbread is shown as a bar model below.
Adding up the number of shares in the bar we have 3+2+1=6
1.2kg is equal to 1200g (multiply by 1000 ).
1200 \div 6=200g per share.
Looking at each ingredient, we have
Flour = 200 \times 3=600g
Butter = 200 \times 2=400g
Sugar = 200 \times 1=200g
Answer: Yes she has enough of each ingredient.
Example 4: ratio to fraction
The diagram below shows the days of the month that were above or below 20^{\circ}C on average.
Complete the bar model to show the fraction of days in the month at were above 20^{\circ}C
By counting the number of days in the month, there are 31 days.
We therefore need to split the bar into 31 equal shares.
The first number in the ratio represents the number of days above 20^{\circ}C and so we need to colour in 11 of these shares in red, the rest are blue.
This means that 11 out of the 31 days were warmer than 20^{\circ}C and so the fraction is \frac{11}{31} .
Solution: \frac{11}{31}
Example 5: problem solving
The ratio of a:b=3:2 . The ratio of b:c=3:5 . What is the ratio of a:c ?
The ratio of a:b=3:2 . The ratio of b:c=3:5 . What is the ratio of a:c ?
Drawing these ratios using bar models, we have:
Instinctively, you may think that the ratio of a:c is 3:5 but this would be incorrect. We need to calculate the ratio of a:c when the number of shares of b are the same for each ratio.
We therefore need to calculate the lowest common multiple of the two values of b, find the equivalent ratios of a:b and b:c when b is the same value, then we can state the ratio a:c.
The first five multiples of 2 and 3 are:
Multiples of 2 = 2, 4, {\color{red} 6}, 8, 10
Multiples of 3 = 3, {\color{red} 6}, 9, 12, 15
LCM(2,3) = {\color{red} 6}.
We now find the equivalent ratios.
Multiplying both parts of the ratio of a:b by 3 , we get the ratio 9:6 .
Multiplying both parts of the ratio of b:c by 2 , we get the ratio 6:10
As the value of b is the same for both ratios, the ratio for a:c can be stated by counting the number of shares in each part.
a:c=9:10 .
This ratio is already in its lowest terms and so cannot be simplified further.
Example 6: ratio scales
A map has the scale of 1cm:2km . The distance between two points on the map is 3.5cm . Calculate the distance between the two points in real life.
Using a bar model, we can show the ratio of the map to the actual distance as
We know that the ratio between the two quantities is 1cm:2km . Remember that these are different units.
Every 1cm on the map represents 2km in real life and so by multiplying the number of shares by 3.5 , we will calculate the actual distance
Here, 3.5cm on the map is equal to 7km in real life.
Common misconceptions
- Ratio written in the wrong order
A common error is to write the parts of the ratio in the wrong order.
E.g.
The number of dogs to cats is given as the ratio 12:13 but the solution is incorrectly written as 13:12 .
- Ratios and fractions confusion
E.g.
The ratio 2:3 is incorrectly expressed as the fraction \frac{2}{3} and rather than the correct answer of \frac{2}{5} .
This is a misunderstanding of the sum of the parts of the ratio. The sum of all of the parts of the ratio gives us the denominator of the fraction.
- Incorrect value for the numerator
A common error is to incorrectly state the numerator from the ratio.
E.g.
The number of mugs to glasses in a kitchen is written as the ratio 8:11 respectively. Write the fraction of mugs in the kitchen.
The solution could be incorrectly written as \frac{11}{19} taking the value for the numerator as the number of glasses, not the number of mugs.
The correct answer is \frac{8}{19} .
- Not fully simplified
A common error is to not write a ratio in its simplest form by not finding the highest common factor.
E.g.
Simplify the ratio 12:18
Dividing both numbers by 2 will leave a ratio of 6:9 . This can be simplified further by dividing by 3 to get the ratio 2:3 , which is the correct answer.
- Not simplifying all parts of the ratio
When simplifying a ratio with more than two parts, not all of the parts are simplified. For example, “Simplify the ratio 12:6:15 ” is incorrectly written as 2:6:3 as the middle part is not cancelled down.
- Dividing the ratio by each part
A common error is to divide a value by each part of the ratio.
E.g.
Divide £120 into the ratio 2:3
The incorrect answer if produced by dividing £120 by 2 , and then dividing £120 by 3 to get £60:£40 .
This does not make sense as the ratio is not equivalent to the original.
The correct answers requires that the amount is divided by the sum of the parts in the ratio
120 \div (2+3)=120 \div 5=£24,
then this value multiplied by each part in the ratio
24 \times 2=£48 ,
24 \times 3=£72
- Mixing units
Make sure that all the units in the ratio are the same.
For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.
- Simplifying the answer
When sharing a quantity into the ratio, you are finding an equivalent ratio so you do not need to simplify the answer.
Practice ratio questions
1. A musical requires 200 costumes. 140 costumes are allocated to the background dancers whilst the rest are for the starring roles. Write the ratio of the costumes for starring roles to backing dancers in the simplest form.




200-140=60 starring role costumes
The ratio is therefore 60:140.
The highest common factor of 60 and 140 is 20:
There are 3 shares for starring roles, and 7 shares for background dancers, hence the ratio 3:7.
2. 50 people were asked about their use of social media; everyone participated. 24 boys were asked. Write the ratio of boys to girls who participated in the study in its simplest form.
Use the bar model below to help you.




Colouring in 24 out of the 50 shares we have
This leaves us with 26 shares that are left white.
The highest common factor of 24 and 26 is 2 .
We can therefore halve the number of shares on each side of the ratio to get
Counting the shares, we now have the ratio of 12:13.
3. A soap “Duo” is made by combining lavender soap with lemon soap. Each bar of soap weighs 330g . If the ratio of lavender to lemon is 4:7 , how many grams of lemon soap are in each bar?




As there are 7+4=11 shares within the ratio
330 \div 11=30g per share
The amount of Lemon in the soap is equal to 7 \times 30=210g
4. The fraction of bananas in a bowl is \frac{13}{20} . Calculate the ratio of bananas to other pieces of fruit in the bowl.




The total number of pieces of fruit is 20 . The number of bananas is 13 . As a bar model, this looks like
The number of other pieces of fruit is therefore 7 (this is calculated by 20-13=7 or counting the number of purple bars above).
The ratio of bananas to other pieces of fruit is therefore 13:7.
5. Mel, Nicole and Orla use a bar model to show their ages.
Orla is 12 years older than Nicole. How old is Mel?




We currently have the ratio 5:6:10.
If Orla is 12 years older than Nicole, and this is 4 shares of the ratio, we have 4 shares equal to 12 years.
1 share is equal to 3 years.
As Mel has 5 shares, 5 \times 3=15 years old.
6. A model soldier is scaled down using a ratio of 5cm:1cm . Given that the height of the soldier in real life is 182cm , calculate the height of the model.




Using a bar model, we have the ratio 5:1 drawn as
If the soldier is 182cm in real life, the value of one share within the bar model is equal to 182 \div 5=36.4cm.
This means the height of the model is 36.4cm.
Ratio GCSE questions
1. An orchestra has 100 musicians. 60\% of them play a string instrument. The ratio of violin players to the other string instruments is 4:11 .
How many musicians play the violin in the orchestra?
(4 marks)
(1)
60 \div (4+11)=4
(1)
4 \times 4=16
(1)
16 violin players
(1)
2. A florist sells 3 sizes of rose bouquets: regular, large, and extra large. The regular bouquet contains 5 roses, the large bouquet contains 8 roses, and the extra large bouquet contains 12 roses.
In one February, she sells 16 regular bouquets, 16 large bouquets and 18 extra large bouquets.
(a) How many roses are required for these orders?
(b) The ratio of roses that were used to not used in the bouquets was 8:3. What fraction of the roses were not used in the bouquets?
(c) How many roses were bought in total?
(5 marks)
(a)
(5 \times 16)+(8 \times 16)+(12 \times 18)
(1)
424 roses
(1)
(b)
\frac{3}{8+3}=\frac{3}{11}
(1)
(c)
424 \div 8 \times 11
(1)
583
(1)
3. During one weekend, 256 planes depart from an airport to go to France and Spain in the ratio of 3:5 . On a bank holiday weekend, the number of flights increases by 68, giving the new ratio of 4:5.
How many more flights went to France on the bank holiday weekend?
(6 marks)
(1)
32 \times 3=9
(1)
256+68=324
(1)
324 \div (4+5)=36
(1)
36 \times 4=144
(1)
144-96=48
(1)
Learning checklist
You have now learned how to:
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.