One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Right angle triangle Pythagoras theorem SOHCAHTOA Substitution Changing the subject of a formula Rearranging equations Fractions Surds

This topic is relevant for:

GCSE Maths Geometry and Measure Trigonometry Exact Trig Values

Table

Trigonometry Table

Here we will learn about the trigonometry table.

There are also trigonometry table worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the trigonometry table?

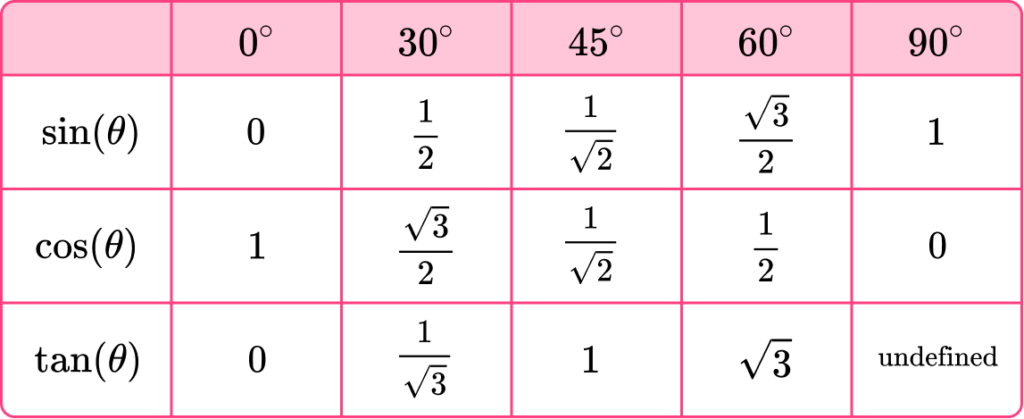
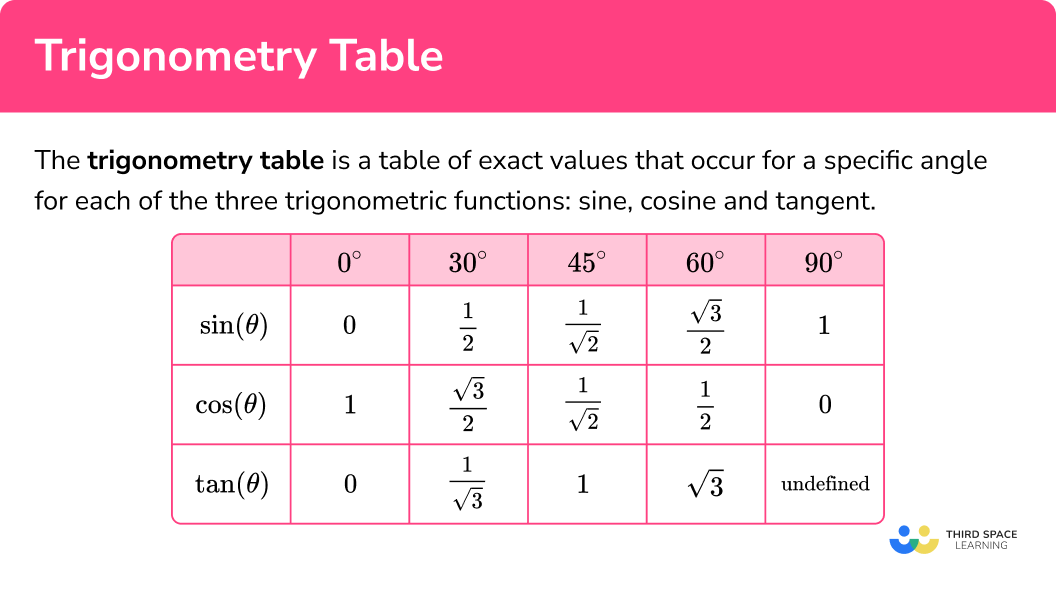
The trigonometry table is a table of exact values that occur for a specific angle for each of the three trigonometric functions – sine, cosine and tangent.

We can use these values to calculate unknown sides, angles and areas of triangles.

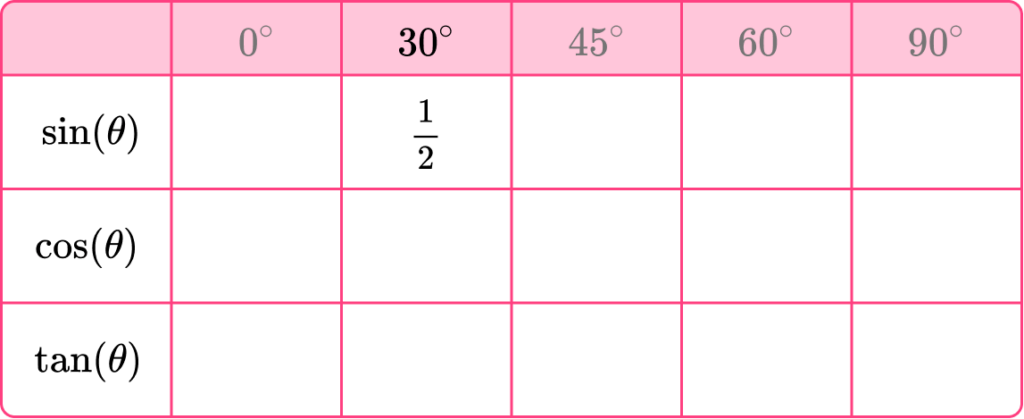
The table below shows the values of trigonometric ratios of standard angles $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ and $90^{\circ}.$

Step-by-step guide: Exact trig values

What is the trigonometry table?

Exact trig values worksheet (includes trigonometry table)

Get your free worksheet of questions and answers covering exact trig values and using the trigonometry table. Includes reasoning and applied questions.

DOWNLOAD FREE

Exact trig values worksheet (includes trigonometry table)

Get your free worksheet of questions and answers covering exact trig values and using the trigonometry table. Includes reasoning and applied questions.

DOWNLOAD FREE

Constructing the trigonometry table

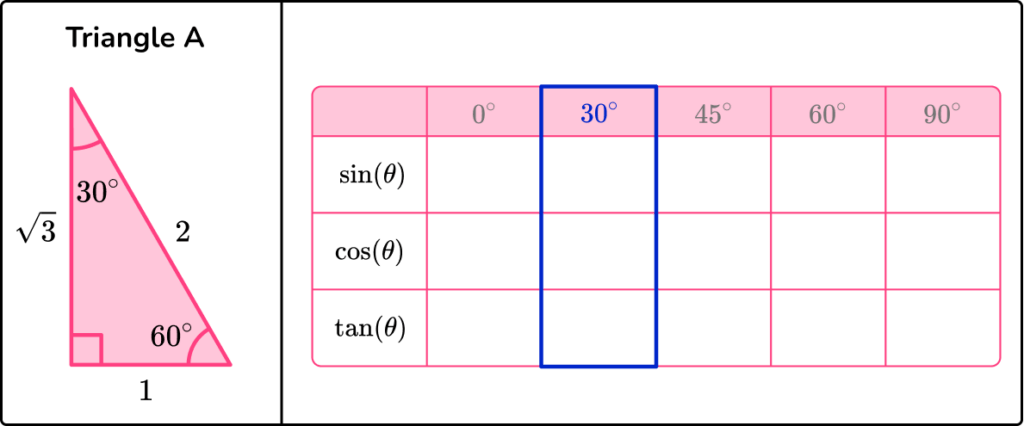
To fill in the table for the exact trig values of $30, 45$ and $60$ degrees, we need to construct two triangles.

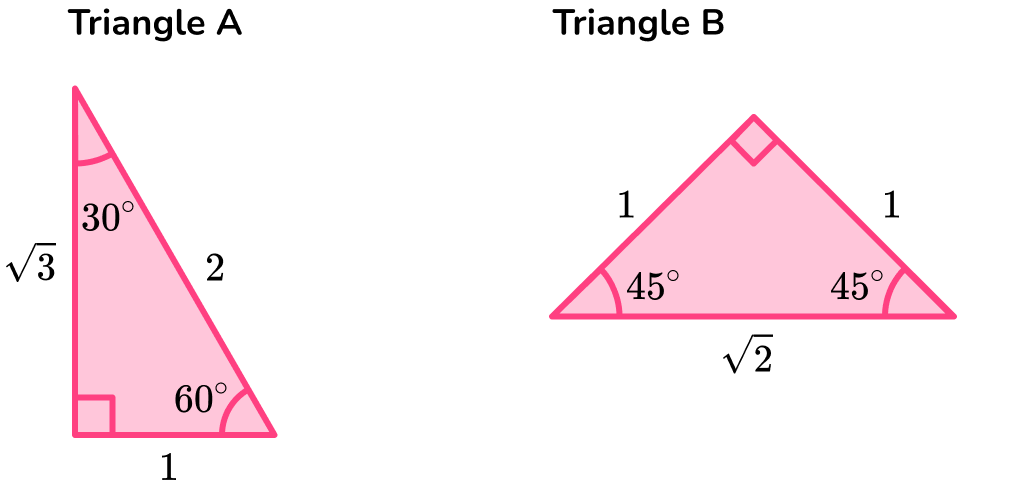
Triangle A has the interior angles of $30^{\circ}, 60^{\circ}$ and $90^{\circ}.$
We will use triangle A to fill in the exact trig values for $30^{\circ}$ and $60^{\circ}.$

Triangle B has the interior angles of $45^{\circ}, 45^{\circ}$ and $90^{\circ}.$
We will use triangle B to fill in the exact trig values for $45^{\circ}.$

Using these triangles and the trig ratios sine, cosine and tangent we can complete the trigonometry table.


$\sin{\theta}=\frac{O}{H}$	$\cos{\theta}=\frac{A}{H}$	$\tan{\theta}=\frac{O}{A}$

Sine of angle $\textbf{θ}$ is the ratio of the opposite and the hypotenuse.

Cosine function of angle $\textbf{θ}$ is the ratio of the adjacent and the hypotenuse.

Tangent function of the angle $\textbf{θ}$ is the ratio of the opposite and the adjacent.

Constructing triangle A

Let us start with how triangle A is constructed.

We start with an equilateral triangle with a side length of $2 \ cm.$ Labelling each side as $2 \ cm$ and each angle as $60^{\circ},$ we have,

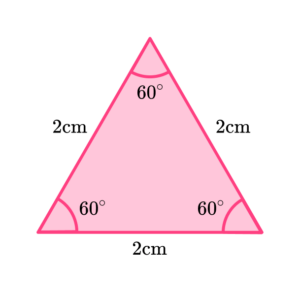
By drawing a vertical line down the middle of the equilateral triangle, we divide it into two identical right-angled triangles.

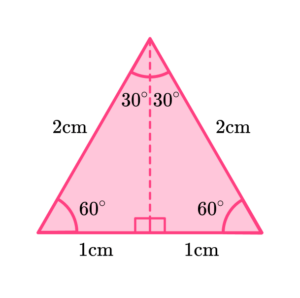
If we look at one of these triangles, we have the following information.

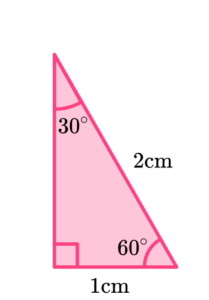
Currently we do not know the height of this right-angled triangle, but we can use Pythagoras’ theorem to determine this length. With $a=x, b=1$ and $c=2,$ we have,

\begin{aligned} c^{2}&=a^{2}+b^{2}\\\\ 2^{2}&=x^{2}+1^{2}\\\\ 4&=x^{2}+1\\\\ x^{2}&=4-1\\\\ x^{2}&=3\\\\ x&=\sqrt{3} \end{aligned}

Step-by-step guide: Pythagoras theorem

This means that the height of the right-angled triangle is the square root of $3 \ cm \ (\sqrt{3} \ cm).$ Labelling this onto the right-angled triangle, we have,

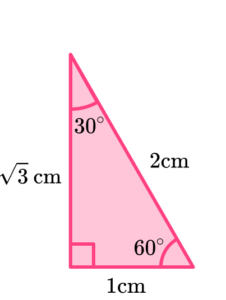
If we were to use a similar triangle, each side length would increase or decrease by the same scale factor, and the angles stay the same. This means that even if we started with an equilateral triangle that had a side length of $x,$ we would be able to obtain exactly the same triangle as above by dividing all of the side lengths by the scale factor.

Constructing triangle B

Now let us look at how triangle B is constructed.

We start with an isosceles right-angled triangle where the two sides with the included $90$ degree angle are the same length of $1 \ cm.$ The two remaining angles in an isosceles triangle are equal and so they must be $45^{\circ}$ each.

Here, the length of the hypotenuse of the triangle is unknown but as with triangle A, we can use Pythagoras’ theorem to determine this length.

As $a=1, b=1$ and $c=x,$ we have,

\begin{aligned} c^{2}&=a^{2}+b^{2}\\\\ x^{2}&=1^{2}+1^{2}\\\\ x^{2}&=1+1\\\\ x^{2}&=2\\\\ x&=\sqrt{2} \end{aligned}

So the length of the hypotenuse of triangle B is $\sqrt{2} \ cm.$

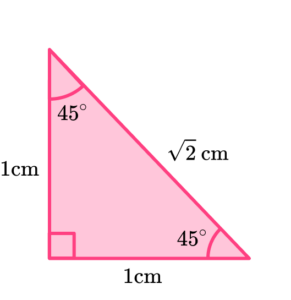
Any similar triangle would enlarge the side lengths, but the angles would stay the same and so any triangle containing these angles will have the same ratio of side lengths.

Step-by-step guide: Trigonometry formula

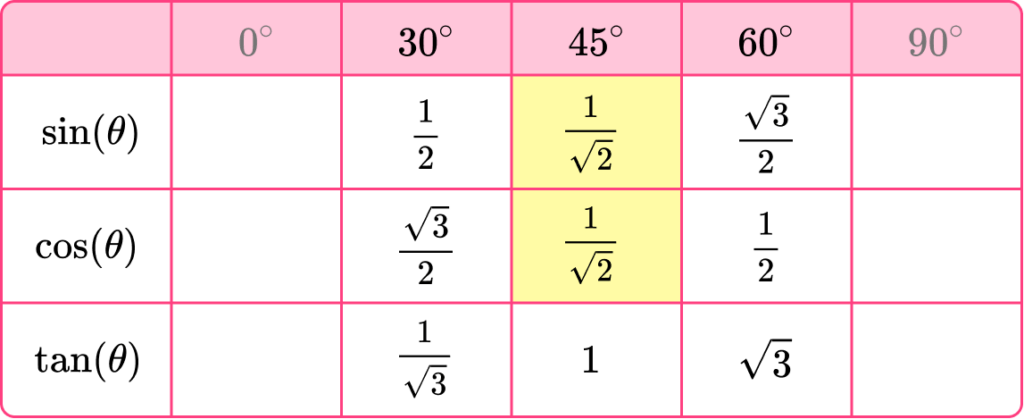
Sin, cos and tan of 30°

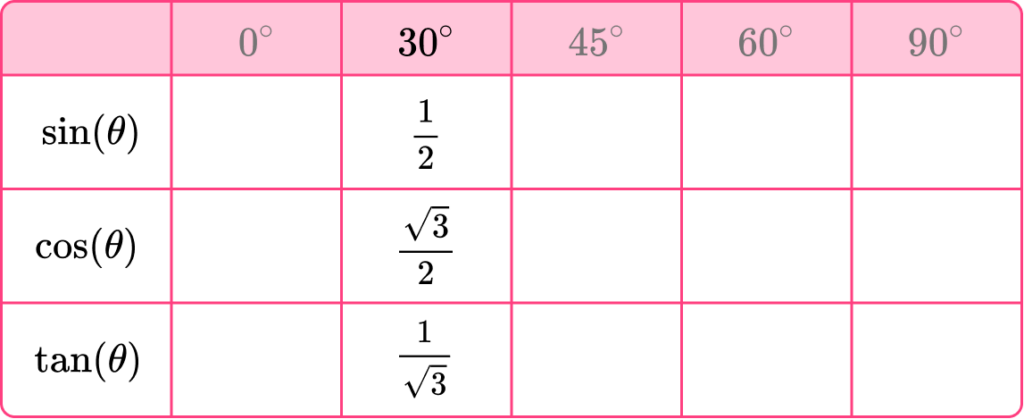
Time to fill in the table of values for the three trig functions of the angles in triangle A, starting with $30^{\circ}.$

Looking at the angle of $30^{\circ}$ we can label the sides $O, A$ and $H,$ accordingly.

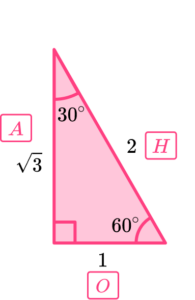
As $\sin(\theta)=\frac{O}{H},$ substituting $\theta=30^{\circ}, O=1$ and $H=2,$ we have $\sin(30)=\frac{1}{2}.$

This means that the exact trigonometric value for $\sin(30)$ is $\frac{1}{2}.$

Continuing this for the cosine of $30^{\circ},$ we have,

$\cos(\theta)=\frac{A}{H},$ and so substituting $\theta=30^{\circ}, A=\sqrt{3}$ and $H=2,$ we have $\cos(30)=\frac{\sqrt{3}}{2}.$

This means that the exact trigonometric value for $\cos(30)$ is $\frac{\sqrt{3}}{2}.$

Finally, for the tangent of $30^{\circ},$ we have,

$\tan(\theta)=\frac{O}{A},$ and so substituting $\theta=30^{\circ}, O=1$ and $A=\sqrt{3},$ we have $\tan(30)=\frac{1}{\sqrt{3}}.$

This means that the exact trigonometric value for $\tan(30)$ is $\frac{1}{\sqrt{3}}.$

Filling in the trigonometry table with these values gives us,

Sin, cos and tan of 60°

Time to fill in the table of values for the three trig functions of the angle $60^{\circ}$ in triangle A.

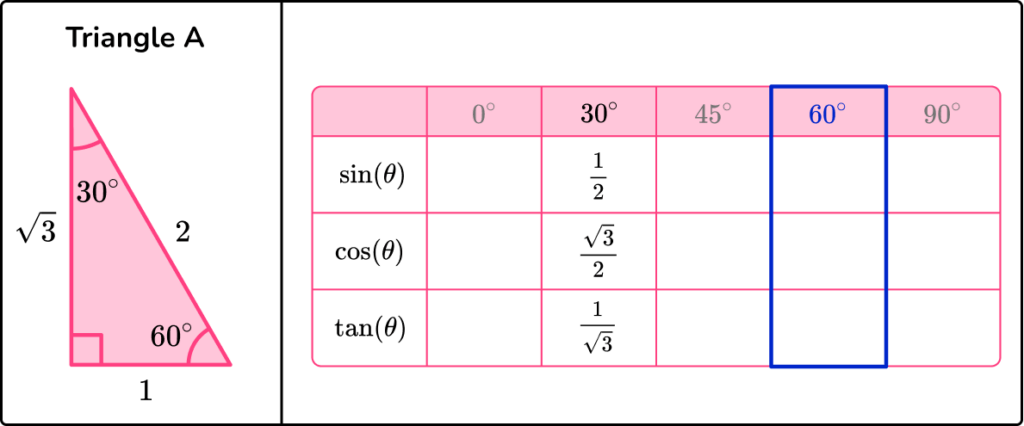
Looking at the angle of $60^{\circ}$ we can label the sides $O, A$ and $H,$ accordingly.

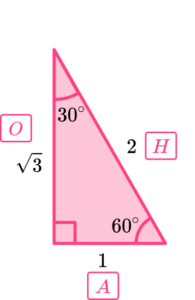
Notice the subtle difference that now the opposite side $O=\sqrt{3}$ and the adjacent side $A=1$ where it was the other way around when we were looking at $30^{\circ}.$ The hypotenuse doesn’t change $(H=2).$

As $\sin(\theta)=\frac{O}{H},$ substituting $\theta=60^{\circ}, O=\sqrt{3}$ and $H=2,$ we have $\sin(60)=\frac{\sqrt{3}}{2}.$

This means that the exact trigonometric value for $\sin(60)$ is $\frac{\sqrt{3}}{2}.$

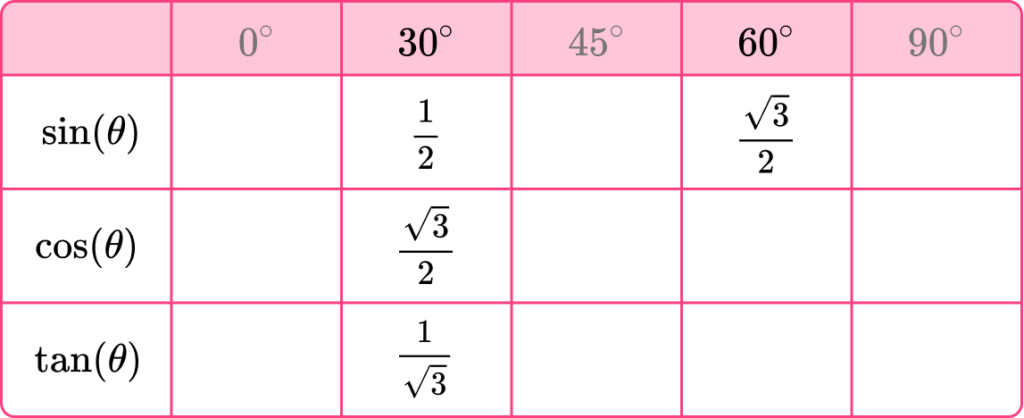
Continuing this for the cosine of $60^{\circ},$ we have

$\cos(\theta)=\frac{A}{H},$ and so substituting $\theta=60^{\circ}, A=1$ and $H=2,$ we have $\cos(60)=\frac{1}{2}.$

This means that the exact trigonometric value for $\cos(60)$ is $\frac{1}{2}.$

Finally, for the tangent of $60^{\circ},$ we have,

$\tan(\theta)=\frac{O}{A},$ and so substituting $\theta=60^{\circ}, O=\sqrt{3}$ and $A=1,$ we have $\tan(60)=\frac{\sqrt{3}}{1}=\sqrt{3}.$

This means that the exact trigonometric value for $\tan(60)$ is $\sqrt{3}.$

Filling in the trigonometric table with these values gives us,

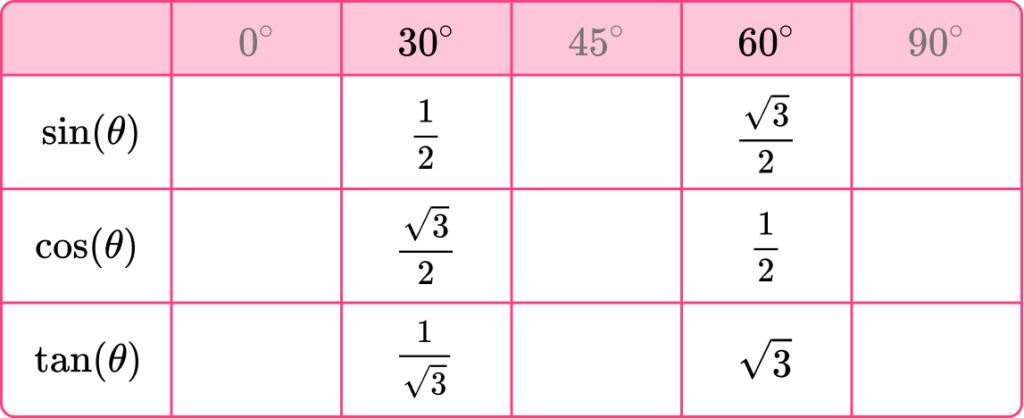
Before we move on to triangle B, let’s quickly look at some common values in the table so far.

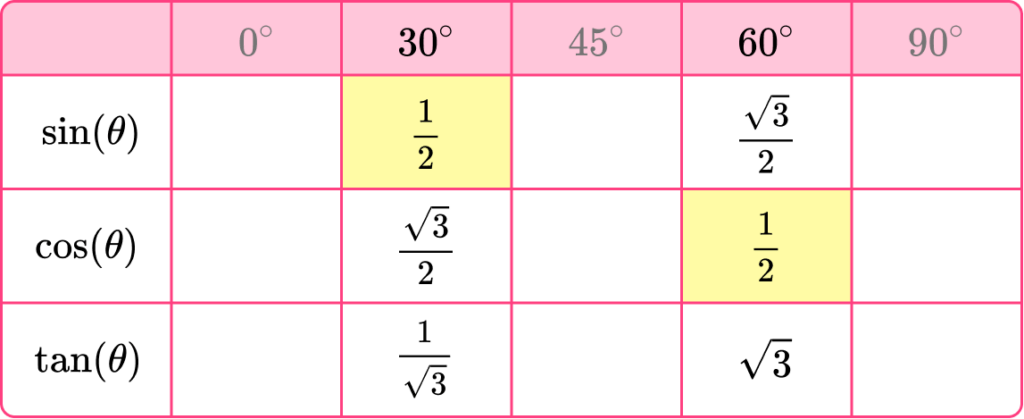
We can see that in the table above, $\sin(30)=\frac{1}{2}$ and $\cos(60)=\frac{1}{2}.$

This means that $\sin(30)=\cos(60).$

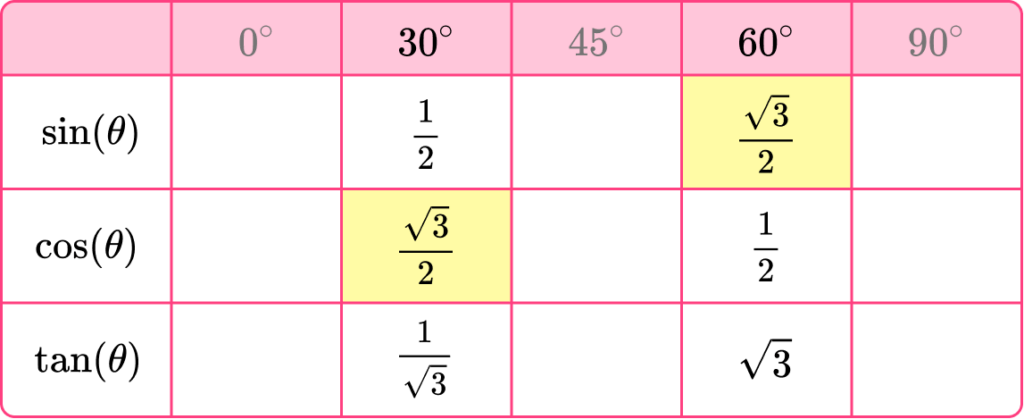
We can also see that $\sin(60)=\frac{\sqrt{3}}{2}$ and $\cos(30)=\frac{\sqrt{3}}{2}.$

This means that $\sin(60)=\cos(30).$

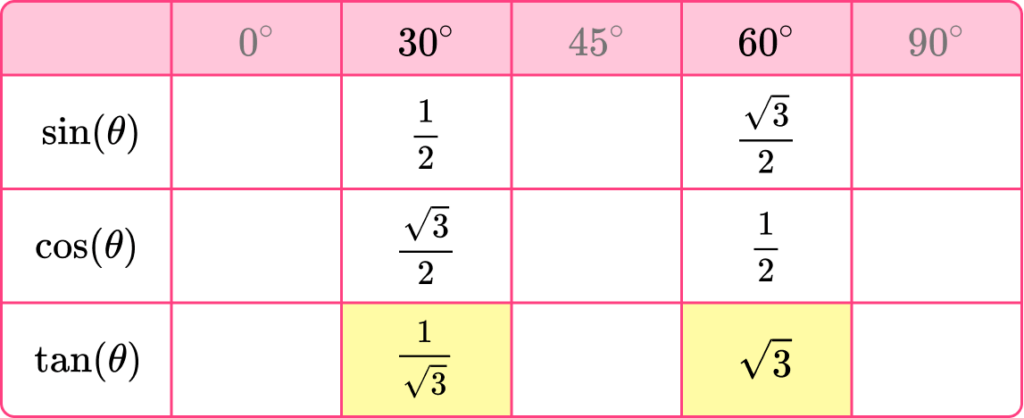
The tangent of $30^{\circ}$ and $60^{\circ}$ are similar in the sense that $\tan(30)=1\div\tan(60)$ (they are the reciprocal of each other).

Sin, cos and tan of 45°

Time to fill in the table of values for the three trig functions of the angle $45^{\circ}$ in triangle B.

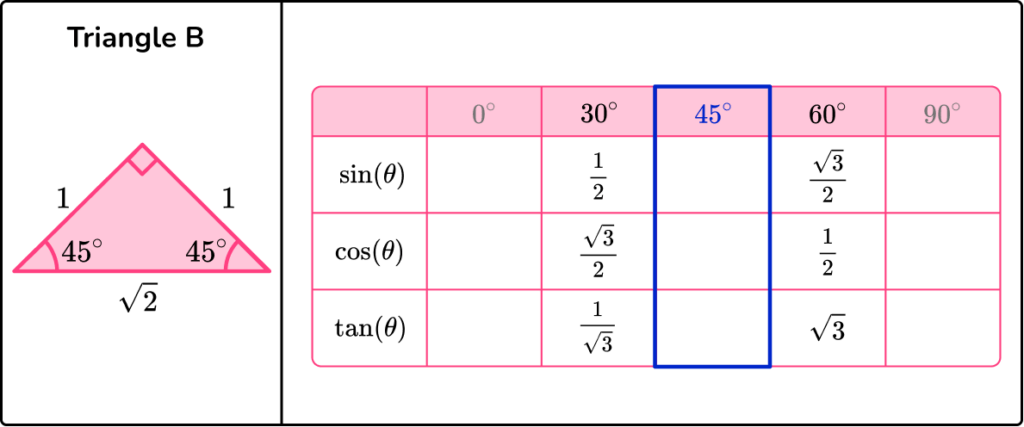
Choosing one of the angles of $45^{\circ}$ (here we have picked the angle at the top of the triangle), we can label the sides $O, A$ and $H,$ accordingly.

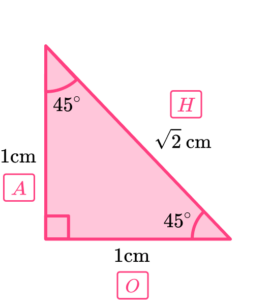
As $\sin(\theta)=\frac{O}{H},$ substituting $\theta=45^{\circ}, O=1$ and $H=\sqrt{2},$ we have $\sin(45)=\frac{1}{\sqrt{2}}.$

This means that the exact trigonometric value for $\sin(45)$ is $\frac{1}{\sqrt{2}}.$

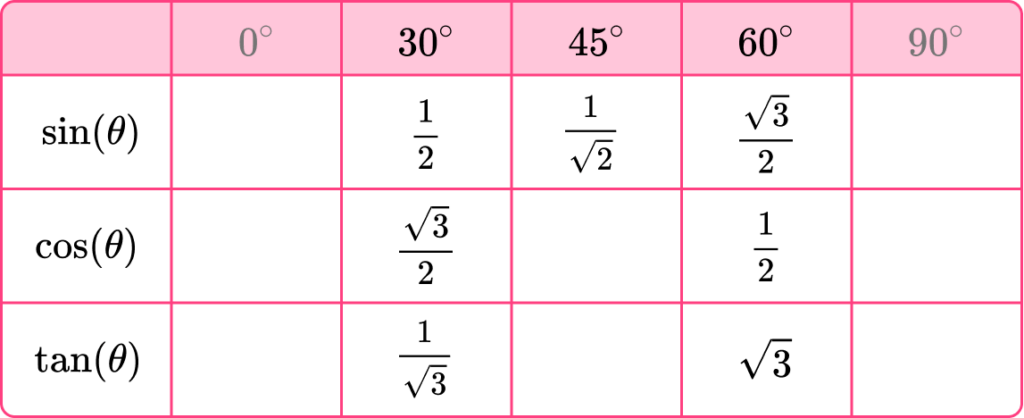
Continuing this for the cosine of $45^{\circ},$ we have

$\cos(\theta)=\frac{A}{H},$ and so substituting $\theta=45^{\circ}, A=1$ and $H=\sqrt{2},$ we have $\cos(45)=\frac{1}{\sqrt{2}}.$

This means that the exact trigonometric value for $\cos(45)$ is $\frac{1}{\sqrt{2}}.$

Finally, for the tangent of $45^{\circ},$ we have

$\tan(\theta)=\frac{O}{A},$ and so substituting $\theta=45^{\circ}, O=1$ and $A=1,$ we have $\tan(45)=\frac{1}{1}=1.$

This means that the exact trigonometric value for $\tan(45)$ is $1.$

Filling in the trigonometry table with these values gives us,

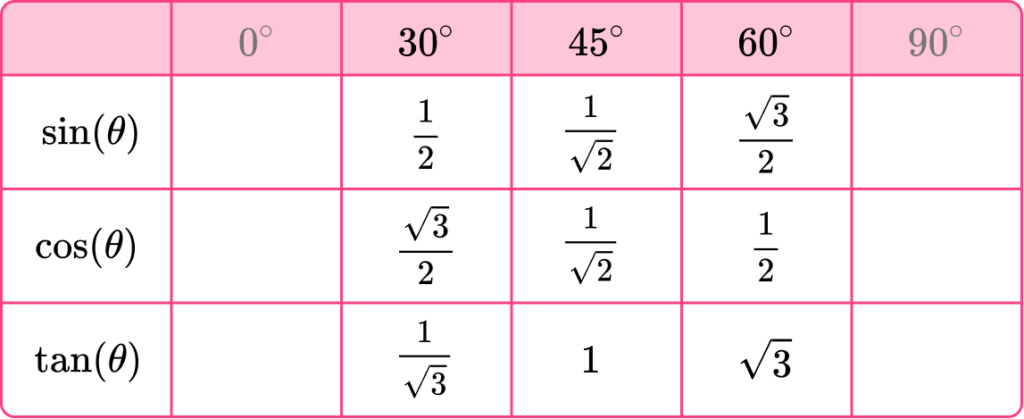
Before we move on to the remaining values in the table, let us briefly inspect these new values.

We can see that in the table above, $\sin(45)=\frac{1}{\sqrt{2}}$ and $\cos(45)=\frac{1}{\sqrt{2}}.$

This means that $\sin(45)=\cos(45).$

Also we have a pleasing value of $\tan(45)=1.$

To briefly summarise what we have found using the table, we have

$\sin(30)=\cos(60)=\frac{1}{2}$
$\sin(60)=\cos(30)=\frac{\sqrt{3}}{2}$
$\tan(60)=\frac{1}{\tan(30)}=\sqrt{3}$
$\sin(45)=\cos(45)=\frac{1}{\sqrt{2}}$

Sin, cos and tan of 0°

For the sine, cosine and tangent of $0^{\circ}$ , we are unable to construct triangles to help us determine these values. This is because a triangle cannot contain an angle of $0^{\circ}$ .

Let’s look at triangle A to try and visualise what happens to the sine, cosine and tangent of the angle $30^{\circ}$ as it gets smaller.

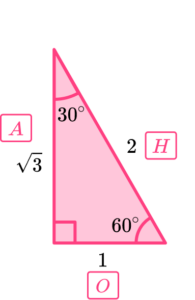
As the $30^{\circ}$ angle at the top gets smaller, the length of the opposite side must get smaller, and the hypotenuse must get shorter as well as it tends towards the length of the adjacent side. This has different outcomes for each trigonometric function.

As $\sin(\theta)=\frac{O}{H}$ and the opposite side is getting smaller (tending towards $0$ ), $\sin(0)$ must also tend towards $0.$ This gives us the value of $\sin(0)=0.$
As $\cos(\theta)=\frac{A}{H}$ and the hypotenuse tends towards the length of the adjacent side, $\cos(0)$ must tend towards $1$ as we would divide the adjacent side by the adjacent side. This gives us the value of $\cos(0)=1.$
As $\tan(\theta)=\frac{O}{A}$ and the opposite side is getting smaller (tending towards $0$ ), $\tan(0)$ must also tend towards $0.$ This gives us the value of $\tan(0)=0.$

Filling in these three values into the first column of the table, we have,

Sin, cos and tan of 90°

Finally we need to consider the sine, cosine and tangent of $90^{\circ}.$ A triangle cannot have two angles that are equal to $90^{\circ}$ but we can consider the sine, cosine and tangent of the angle as it increases. If we still used triangle A but this time we will refer to the angle of $60^{\circ}$ and increase the size of the angle towards $90^{\circ}.$

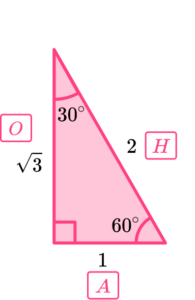
As the $60^{\circ}$ angle at the bottom gets larger, the length of the opposite side must get longer, and the hypotenuse must get longer as well as it tends towards the length of the opposite side. This has different outcomes for each trigonometric function.

As $\sin(\theta)=\frac{O}{H}$ and the hypotenuse is tending towards the length of the opposite side, $\sin(90)$ must also tend towards $1$ as we would divide the opposite side by the opposite side. This gives us the value of $\sin(90)=1.$
As $\cos(\theta)=\frac{A}{H}$ and the hypotenuse is getting longer, $\cos(0)$ must tend towards $0$ as we would divide the adjacent side by a very large value for the hypotenuse, making the result incredibly small, as if it were $0.$ This gives us the value of $\cos(90)=0.$
As $\tan(\theta)=\frac{O}{A}$ and the opposite side is getting longer, $\tan(90)$ is undefined as when we divide a very large number (the opposite) by a relatively small number (the adjacent), this can have little impact on the very large number. In fact, the value could be infinitely large. This means that the value of $\tan(90)$ we use is undefined (we cannot give this a value).

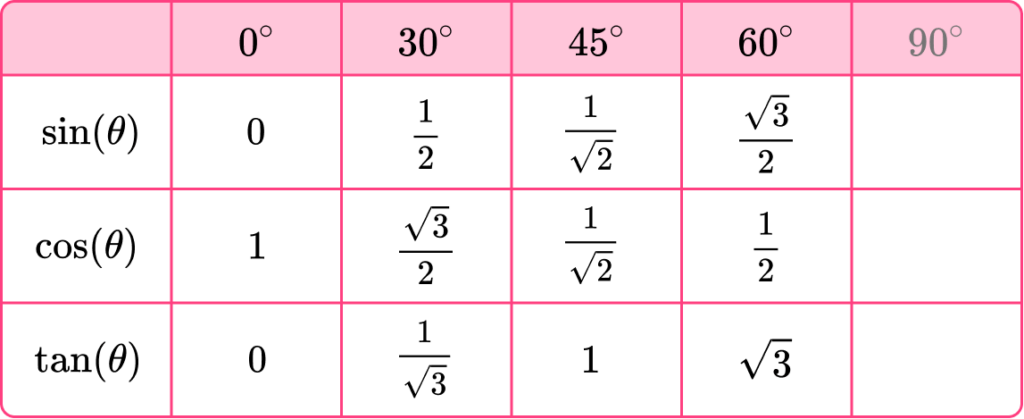
Filling in these three values into the table, we have the final trigonometry table.

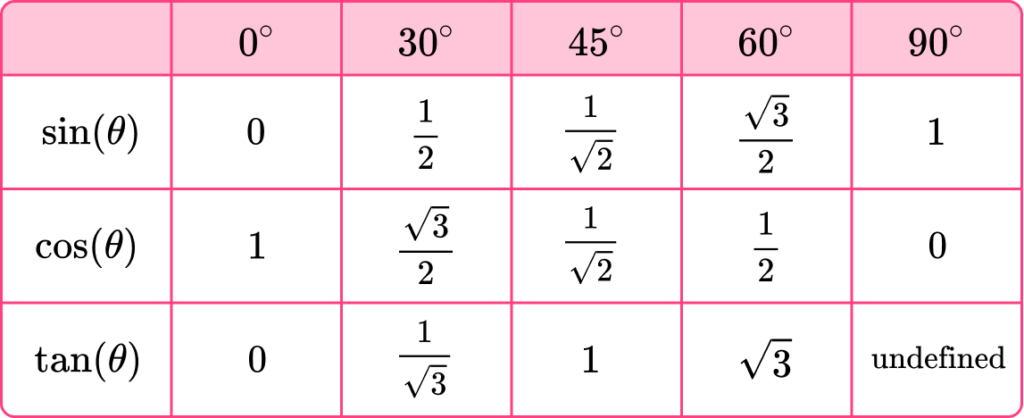
By looking at the table, we can now spot some other values that are the same for different trigonometric functions, including

$\sin(0)=\cos(90)=\tan(0)=0$
$\sin(90)=\cos(0)=\tan(45)=1$

How to use the trigonometry table

In order to calculate using exact trig values from the trigonometry table:

Recall the exact trig value from the table.
Substitute values into the equation / expression.
Solve the equation / simplify the expression fully.

Explain how to use the trigonometry table

Trigonometry table examples

Example 1: multiplying an exact trig value by an integer

Calculate the exact value of $4\cos(30).$

Recall the exact trig value from the table.

The exact trig value of $\cos(30)=\frac{\sqrt{3}}{2}.$

2Substitute values into the equation / expression.

Substituting the value of $\cos 30$ into this expression, we have $4\cos(30)=4\times\frac{\sqrt{3}}{2}.$

3Solve the equation / simplify the expression fully.

4\times\frac{\sqrt{3}}{2}=\frac{4\sqrt{3}}{2}=2\sqrt{3}

Example 2: simplifying expressions using the trigonometry table

Simplify the expression $2\sin(45)\cos(45)-4\sin(30).$

Recall the exact trig value from the table.

The exact trig value of $\sin(45)=\frac{1}{\sqrt{2}}.$

The exact trig value of $\cos(45)=\frac{1}{\sqrt{2}}.$

The exact trig value of $\sin(30)=\frac{1}{2}.$

Substitute values into the equation / expression.

Substituting the value of $\sin{45},$ the value of $\cos{45}$ and the value of $\sin{30}$ into the expression, we have

$2\sin(45)\cos(45)-4\sin(30)=2\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}-4\times\frac{1}{2}.$

Solve the equation / simplify the expression fully.

\begin{aligned} &2\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}-4\times\frac{1}{2}\\\\ =&2\times\frac{1}{2}-2\\\\ =&1-2\\\\ =&-1 \end{aligned}

$2\sin(45)\cos(45)-4\sin(30)=-1$

Example 3: dividing a surd by an exact trig value

Calculate the value of $\frac{2\sqrt{2}}{\cos(45)}.$

Recall the exact trig value from the table.

The exact trig value of $\cos(45)=\frac{1}{\sqrt{2}}.$

Substitute values into the equation / expression.

Substituting this into the expression, we have

$2\sqrt{2}\div\frac{1}{\sqrt{2}}.$

Solve the equation / simplify the expression fully.

\begin{aligned} &2\sqrt{2}\div\frac{1}{\sqrt{2}}\\\\ =&2\sqrt{2}\times\sqrt{2}\\\\ =&2\times\sqrt{4}\\\\ =&2\times{2}\\\\ =&4 \end{aligned}

The value of $\frac{2\sqrt{2}}{\cos(45)}=4.$

Example 4: calculating with three exact trig values

Calculate the exact value of $\sin(30)+\cos(60)-\tan(45).$

Recall the exact trig value from the table.

The exact trig value of $\sin(30)=\frac{1}{2}.$

The exact trig value of $\cos(60)=\frac{1}{2}.$

The exact trig value of $\tan(45)=1.$

Substitute values into the equation / expression.

Substituting these into the expression, we have

$\sin(30+\cos(60)-\tan(45)=\frac{1}{2}+\frac{1}{2}-1.$

Solve the equation / simplify the expression fully.

\frac{1}{2}+\frac{1}{2}-1=1-1=0

$\sin(30)+\cos(60)-\tan(45)=0$

Example 5: solving equations with exact trig values

Given that $x=\cos(30),$ solve the equation $3y=(2x)^{2}.$

Recall the exact trig value from the table.

Using the trigonometry ratios table, the exact trig value of $\cos(30)=\frac{\sqrt{3}}{2}.$

Substitute values into the equation / expression.

Substituting this into the equation $3y=(2x)^{2},$ we have

$3y=(2\times\frac{\sqrt{3}}{2})^{2}.$

Solve the equation / simplify the expression fully.

\begin{aligned} 3y&=(2\times\frac{\sqrt{3}}{2})^{2}\\\\ 3y&=(\sqrt{3})^{2}\\\\ 3y&=3\\\\ y&=1 \end{aligned}

Example 6: solving equations with exact trig values

Given that $x=\sin(45)$ and $y=\cos(45),$ determine the value of $\theta$ of the equation $\tan(\theta)=\frac{x}{y}.$

Recall the exact trig value from the table.

The exact trig value of $\sin(45)=\frac{1}{\sqrt{2}}.$

The exact trig value of $\cos(45)=\frac{1}{\sqrt{2}}.$

Substitute values into the equation / expression.

Substituting these values into the equation, we have

$\tan(\theta)=\frac{1}{\sqrt{2}}\div\frac{1}{\sqrt{2}}.$

Solve the equation / simplify the expression fully.

$\frac{1}{\sqrt{2}}\div\frac{1}{\sqrt{2}}=1$ and so we now have the equation $\tan(\theta)=1.$

As $\tan(45)=1$ from the trig table, we can state that

$\theta=45^{\circ}.$

Note that algebraically we would write the inverse $\tan$ of $1$ is $45 \ (\tan^{-1}(1)=45^{\circ}).$

Common misconceptions

Exact values

If you are asked for an exact value, you must leave your answer in surd form.

There is no need to write your answer as a decimal and round. It would no longer be an exact value.

Using exact values

If you have been given the answer, you need to make it clear that you have used the exact trig value in your workings.

Practice trigonometry table questions

0^{\circ}

30^{\circ}

45^{\circ}

90^{\circ}

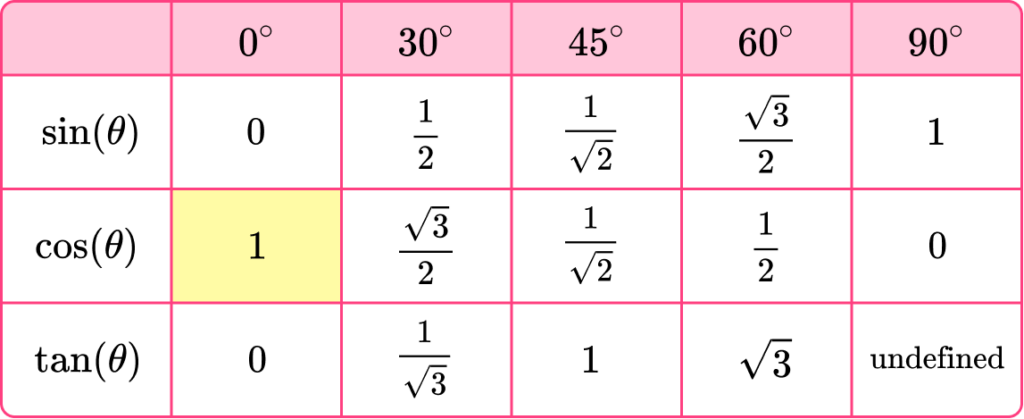
Trigonometry Table question 1

3+\sqrt{3}

4

3+\frac{2}{\sqrt{3}}

195

2\sin(30)=2\times\frac{1}{2}=1.

3\tan(45)=3\times{1}=3.

1+3=4.

\frac{1}{3}

\frac{1}{2}

0.95\text{ (2dp)}

3

\cos(30)=\frac{\sqrt{3}}{2}

\frac{\sqrt{3}}{2}\div\sqrt{3}=\frac{\sqrt{3}}{2}\times\frac{1}{\sqrt{3}}=\frac{1}{2}

2

1+\sqrt{3}

2\sqrt{3}

180

2(\cos(30)+\sin(60))-\tan(0)=2(\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2})-0=2\sqrt{3}

5

34

106

10

2y=(6\tan(30))^{2}-2

2y=(6\times\frac{1}{\sqrt{3}})^{2}-2

2y=\frac{36}{3}-2

2y=12-2=10

Therefore $y=5$ .

0^{\circ}

45^{\circ}

60^{\circ}

90^{\circ}

\sin(\theta)=4\sin(30)\cos(60)=4\times\frac{1}{2}\times\frac{1}{2}=1

$\sin(90)=1$ and so $\theta=90^{\circ}.$

Trigonometry table GCSE questions

1. Complete the table of exact trigonometric values for the angles of $30^{\circ}$ and $60^{\circ}.$

Trigonometry Table GCSE Question 1

(4 marks)

Show answer

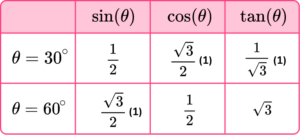
Trigonometry Table GCSE Question 1 Answer

(4)

2. James sketches the right-angled triangle used to generate the exact trig values for the sine, cosine and tangent of $45^{\circ}.$ His sketch is drawn below.

(a) State the mistake that James has made with his sketch.

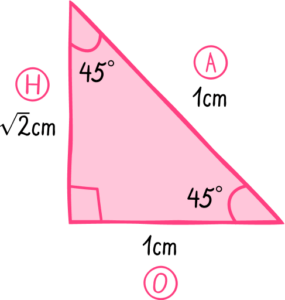
Trigonometry table GCSE question 2

(b) Calculate the actual area of the triangle that James was meant to sketch.

(3 marks)

Show answer

(a)

Any of the following.

He has mislabelled the hypotenuse as the perpendicular height.

The perpendicular height is longer than the hypotenuse $(\sqrt{2}$ and $1).$

The adjacent side should be the perpendicular height.

The hypotenuse should be the side opposite the right angle.

The two perpendicular sides should be the same length.

The side adjacent to the $45^{\circ}$ angle at the top is the perpendicular height.

(1)

(b)

1\times{1}\div{2}

(1)

0.5 \ cm^{2}

(1)

3. Triangles $ABE$ and $ACD$ are similar.

$AB = 1 \ cm$
$BE = 0.5 \ cm$
$CD = 1 \ cm$
Angle $ABE = 60^{\circ}$

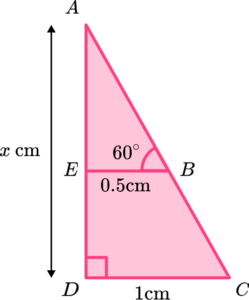
Trigonometry table GCSE question 3

Determine the length of the line $AE = x \ cm.$

(5 marks)

Show answer

\tan(60)=\sqrt{3}

(1)

AE=0.5\times \sqrt{3}=\frac{\sqrt{3}}{2}

(1)

Scale factor is $1\div 0.5=2$ .

(1)

x=AD=2\times \frac{\sqrt{3}}{2}

(1)

x=\sqrt{3}

(1)

Learning checklist

You have now learned how to:

Know the exact values of

\sin \theta

and

\cos \theta

for

\theta = 0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}

and

90^{\circ}

; know the exact value of

\tan \theta

for

\theta = 0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}

The next lessons are

Beyond GCSE

Other trigonometric functions covered at A level include,

Secant
The secant function $(sec)$ is $1$ divided by the cosine of an angle.

Cosecant
The cosecant function $(cosec)$ is $1$ divided by the sine of an angle.

Cotangent
The cotangent function $(cot)$ is $1$ divided by the tangent of an angle.

We also use a different unit of measure for angles called radians.

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.