One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Properties of 2D shapes
Plotting coordinates
Straight line graphsParallel and perpendicular lines
Graphs of other functions
This topic is relevant for:
Lines of Symmetry
Here we will learn about lines of symmetry, including symmetry properties within polygons, angle properties, and symmetry of different line graphs.
There are also lines of symmetry worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are lines of symmetry?
Lines of symmetry are straight lines that divide a shape into two equal parts where one part is an exact reflection of the other.
E.g.
A rectangle has two lines of symmetry (LoS) shown below using a dashed line. In the diagram on the left, the vertical line of symmetry splits the rectangle into two equal shapes, in the diagram on the right the horizontal line of symmetry splits the rectangle into two equal shapes.
If you imagine folding these rectangles along the line of symmetry, both sides will match perfectly.
To draw a line of symmetry, you need to locate the position where you can split the shape into two equal parts. This can be described as a mirror image.
What are lines of symmetry?
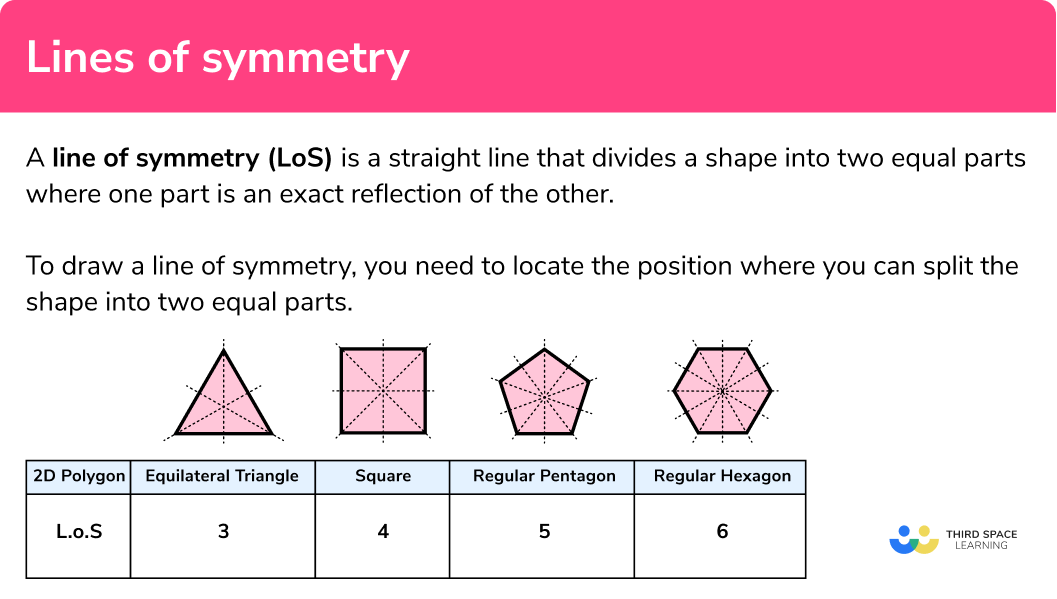
Lines of symmetry in regular shapes
Many 2D shapes have lines of symmetry.
Regular polygons all share the property that the number of sides is equal to the number of lines of symmetry.
Below is a couple of examples of these cases:
A reason why regular shapes have many lines of symmetry is due to the angles within the shape being the same.
Lines of symmetry in irregular shapes
As soon as the angles in two-dimensional shapes change from their equal property, the number of lines of symmetry changes.
Let’s look at different shapes (specifically quadrilaterals) and their number of lines of symmetry.
The parallelogram is an interesting case because although it has set angle properties (the opposing angles are equal), they do not contain any lines of symmetry.
They do however have rotational symmetry (see the lesson on rotational symmetry for more information).
It is important to note that the different orientations of each quadrilateral above will still result in the same number of lines of symmetry.
For example, if the kite rotates 90 degrees clockwise about it’s centre, the line of symmetry will still be the longest diagonal as the line of symmetry moves with the shape. Also, lines of symmetry do not have to go through two vertices.
Lines of symmetry in graphs
We don’t stop at shapes when we look at lines of symmetry, we can also consider lines of symmetry with different types of graphs.
E.g.
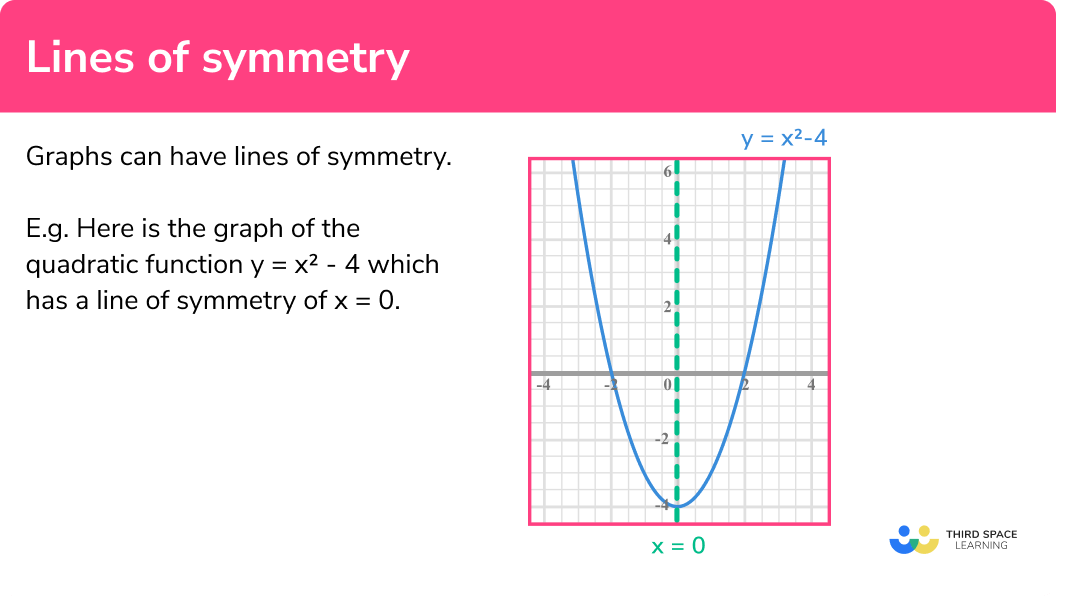
Below is the graph of the equation y=x^2-4:
Here we can see that the y -axis is a line of symmetry because the graph would be symmetrical for each point of the curve. This is a really useful tool when drawing quadratic graphs because each point on the curve will be symmetrical with another.
Furthermore, we can express the line of symmetry to be the line x=0 as this is the equation of the vertical line for all points when x=0.
For more information on equations of straight line graphs, see the lesson equation of a line.
A straight line also has a line of symmetry. Take the straight line y=x:
If we constructed a line of symmetry at the origin, the line would be perpendicular (at 90 degrees to) the original line. The equation of this line is y=-x.
As the line continues to infinity in each direction, the two halves of the bisected line are the same length.
For more information on perpendicular lines, see the lesson parallel and perpendicular lines (coming soon).
Lines of symmetry in graphs
Lines of symmetry in circles
A regular hexagon has 6 lines of symmetry, a decagon has 10 lines of symmetry, and an icosagon has 20 lines of symmetry. But what about a circle?
A circle can be rotated around its centre and the shape will remain identical as the radius is the same for every point.
The diameter of a circle splits the circle into two equal sized semicircles. The diameter can be placed anywhere in the circle and by its definition, it must go through the centre of the circle so we will always have two equal parts.
This mirror symmetry can therefore be viewed along any diameter and so the circle is said to have infinite lines of symmetry.
How to draw lines of symmetry
In order to draw lines of symmetry:
- Locate the centre of the 2D shape.
- Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
- Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
Explain how to draw lines of symmetry
Lines of symmetry worksheet
Get your free lines of symmetry worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE Lines of symmetry worksheet
Get your free lines of symmetry worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREELines of symmetry examples
Example 1: the equilateral triangle
Draw all of the lines of symmetry for the equilateral triangle below:
- Locate the centre of the 2D shape.
Draw a small x in the centre of the triangle:
2Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
Here we can draw a vertical line as this divides the shape into two identical right angle triangles (one is a reflection of the other):
3Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
As the shape has an odd number of vertices, we need to pass through a vertex with the opposing side. We cannot pass through opposing vertices as they don’t exist for this shape.
The equilateral triangle has 3 lines of symmetry.
Example 2: the regular pentagon
Draw all of the lines of symmetry for a regular pentagon:
Locate the centre of the 2D shape.
Draw a small x in the centre of the pentagon (this does not have to be exact):
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
Here we can draw a vertical line as this divides the shape into two identical shapes (one is a reflection of the other):
Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
As the shape has an odd number of vertices, we need to pass through a vertex with the opposing side.
The regular pentagon has 5 lines of symmetry.
Example 3: using angles
Show that the hexagon below has no lines of symmetry.
Locate the centre of the 2D shape.
Draw a small x in the centre of the hexagon (this does not have to be exact):
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
Imagine drawing a line from A to D . If this is a line of symmetry then the angles B and F, and C and E must be equal to one another. As C and E are not equal to each other, the line AD is not a line of symmetry.
Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
As the shape has an even number of vertices, we need to pass through opposite vertices and then pass through opposing sides. When we pass through opposing vertices, we get:
When we pass through opposing sides, we get:
As there is no line that can be drawn through opposing vertices or sides of the shape that splits the shape into two reflected parts, this shape has no lines of symmetry.
Example 4: angle facts
Use angle facts to find the number of lines of symmetry in the following shape ABCDEF:
Locate the centre of the 2D shape.
To find the centre of the shape, join the diagonals together. Here we have:
Despite the centre being outside the shape, we can use it to locate lines of symmetry. Next we need to calculate all of the interior angles of the shape to see if they can help us spot any lines of symmetry.
Angle CDE =180-45=135^o (angles on a straight line total 180^o )
Angle CFE = Angle CFA = (360-90) \div 2 = 135^o (angles at a point total 360^o )
Angle DEF = Angle BAF = 180-135 = 45^o (supplementary to angle CDE )
Angle BCF = Angle DCF = 90\div2 = 45^o
We now have the following information:
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
By sketching a vertical and horizontal line through the centre, we can see that the shape does not have a line of symmetry in either of these directions.
Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
By rotating the ruler around the centre, we can see that the line CF splits the shape ABCDEF in half. Looking at the angles on either side of the line of symmetry, we can see that the angles at B and D , and the angles at A and E are the same.
As the other two angles are bisected, the line CF is the only line of symmetry in this shape.
Example 5: quadratic graph
Write the equation of the line of symmetry for the quadratic equation y=x^2+6x+8. :
Locate the centre of the 2D shape.
Here, rather than locating the centre, we are going to locate the turning point of the curve. The turning point is the point on the curve where the gradient changes from positive to negative, or viceversa.
For the graph of y=x^2+6x+8 , we can see that the turning point is at (-3,-1) however for questions without a visual representation, the turning point can be calculated by completing the square:
\begin{aligned} &y=(x+3)^2-9+8\\\\ &y=(x+3)^2-1 \end{aligned}
Turning point: (-3,-1) .
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
Here we can see that if we sketch a vertical line through the turning point (-3,-1) , the coordinates on either side of this line are the same distance away from the line.
This means that the vertical line that intersects the x axis at -3 is a line of symmetry, or x=-3.
Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
By rotating the ruler around the turning point, there are no other lines that show a symmetry in the graph of y=x^2+6x+8 . The only line of symmetry therefore is x=-3 .
Example 6: reciprocal graph
State the equation of the lines of symmetry for the equation y=\frac{4}{x} .
Locate the centre of the 2D shape.
The graph of y=\frac{4}{x} has two asymptotes. Asymptotes are lines that are reached when a value is undefined, in this case when x=0, or y=0 . This is because, as the value of x gets larger (in the positive or negative direction), the value of y gets closer to zero.
This is also true as the value of x tends towards zero as we will be dividing 4 by a very small number, leaving us with an infinitely large value of y. The importance of this fact allows us to locate the “centre of the graph”. For this graph, the centre is at (0,0) .
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
Let us talk about the graph using the four quadrants:
If you place your ruler on the y -axis, we can see that Quadrants 1 and 4 are not symmetrical to Quadrants 2 and 3 . If we do the same with the x -axis, Quadrants 1 and 2 are not symmetrical to Quadrants 3 and 4 . So this graph has no horizontal or vertical lines of symmetry.
Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices
As we rotate the line of symmetry around the centre point, we can see that when we reach an angle of 45 degrees, the two sides of the line are symmetrical. The equation of this line is y=x.
If we continue rotating, we get to 135 degrees. This is the line y=-x . This means that the graph of y=\frac{4}{x} has two lines of symmetry:
\begin{aligned} &y=x\\\\ &y=-x \end{aligned}
Common misconceptions
- Rotational symmetry
Lines of symmetry are mixed up with rotational symmetry. A line of symmetry divides the shape equally into two symmetrical pieces. A rotational symmetry is the number of times a shape fits into itself when rotated around its centre.
- The diagonals of quadrilaterals
The diagonals of a quadrilateral are often incorrectly joined together and highlighted as a line of symmetry. The only quadrilateral where this is true is the square.
E.g.
Below is the example for an incorrect line of symmetry for a rectangle.
- The number of sides = the order of lines of symmetry
Although this is true for regular shapes, this is not true for all shapes.
Related lessons
Lines of symmetry is part of our series of lessons to support revision on symmetry. You may find it helpful to start with the main symmetry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Practice lines of symmetry questions
1. Calculate the number of lines of symmetry for the kite below.
2. Calculate the number of lines of symmetry for a hexagon.
3. How many lines of symmetry does the octagon below have?
4. Calculate the number of lines of symmetry for the shape ABCDEFG .
5. State the equation of the line of symmetry for the graph y=x^2+20x-90
6. The graph of y=-\frac{1}{x} has two lines of symmetry. One of these lines is y=x . State the equation of the other line of symmetry.
Lines of symmetry GCSE questions
1. ABCD is a quadrilateral. Lines AB and CD are parallel. By finding the value for x , show that the shape has one line of symmetry.
(5 marks)
2x+10+66=180
(1)
2x=104 so x=52^o
(1)
2\times52+10=114^o and 52+14=66^o
(1)
As angle BAD = ABC and angle ADC = BCD, ABCD is an isosceles trapezium with 1 vertical line of symmetry.
(1)
(1)
2.
(a) Complete table of values for the quadratic y=x^2+4x-10.
\begin{aligned}
&x \quad -2 \quad -1 \quad\quad 0 \quad\quad 1 \quad\quad 2 \quad\quad 3 \\
&y \quad \quad \;\: \quad-3 \quad\quad 0 \quad\quad 1
\end{aligned}
(b) Use the table to state the equation of the line of symmetry for the equation y=x^2+4x-10.
(5 marks)
(a)
\begin{aligned} &x \quad -2 \quad -1 \quad\quad 0 \quad\quad 1 \quad\quad 2 \quad\quad 3 \\ &y \quad -8 \quad -3 \quad\quad 0 \quad\quad 1 \quad\quad 0 \quad \;\: – 3 \end{aligned}
(3)
(b)
The values of y are symmetrical around the point (1,1)
(1)
x=1
(1)
3. Calculate the equation of the line of symmetry for the line y=2x+3 at the point (2,7) .
(3 marks)
Perpendicular gradient m=-0.5
(1)
y=-0.5x+c at (2,7) means 7=-0.5 \times 2+c, \;c=8
(1)
y=-0.5x+8
(1)
Learning checklist
You have now learned how to
- Identify lines of symmetry in 2D shapes presented in different orientations
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.