One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
2D shapes Coordinates maths Straight line graphs Parallel and perpendicular lines Types of graphsThis topic is relevant for:

Rotational Symmetry
Here we will learn about rotational symmetry, including rotational symmetry within polygons, angle properties, and symmetry of different line graphs.
There are also rotational symmetry worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is rotational symmetry?
Rotational symmetry is the number of times a shape can “fit into itself” when it is rotated 360 degrees about its centre.
E.g.
A rectangle has a rotational symmetry of order 2 shown below where one vertex is highlighted with a circle and the centre of the shape is indicated with an ‘x’. In the diagram, the shape looks identical in two orientations and so the rotational symmetry of the rectangle is 2.
To calculate the order of rotational symmetry of a shape, you need to locate the centre of the shape.
If the polygon has an even number of sides, this can be done by joining the diagonals. If the polygon has an odd number of sides, this can be done by joining each vertex to the midpoint of the opposing side.
You then rotate the shape 360 degrees around the centre and see how many times the shape looks exactly like the original.
What is rotational symmetry?
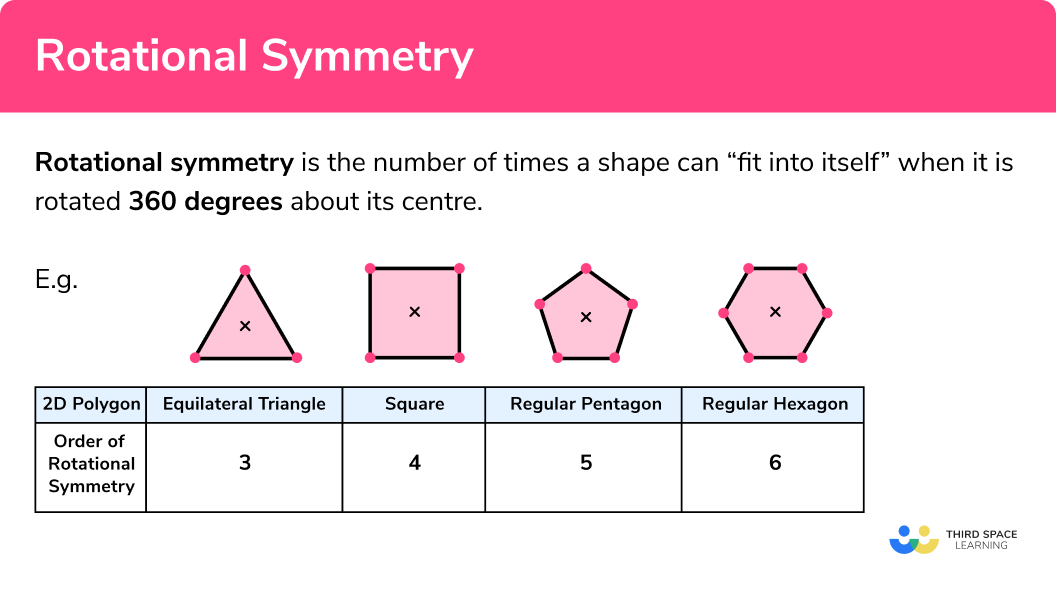
Rotational symmetry in regular shapes
Many 2D shapes have a rotational symmetry. If a shape is rotated around its centre and the shape returns to the original position without it “fitting into itself”, then the shape is described to have no rotational symmetry. Irregular shapes tend to have no rotational symmetry. Regular polygons have the same number of sides as their rotational symmetry.
A reason why regular shapes have the same number of sides as their rotational symmetry is due to the angles and side lengths within the shape being the same.
Rotational symmetry in irregular shapes
As soon as the angles in two-dimensional shapes change from their equal property, the order of rotational symmetry changes.
Let’s look at different shapes (specifically quadrilaterals) and their order of rotational symmetry.
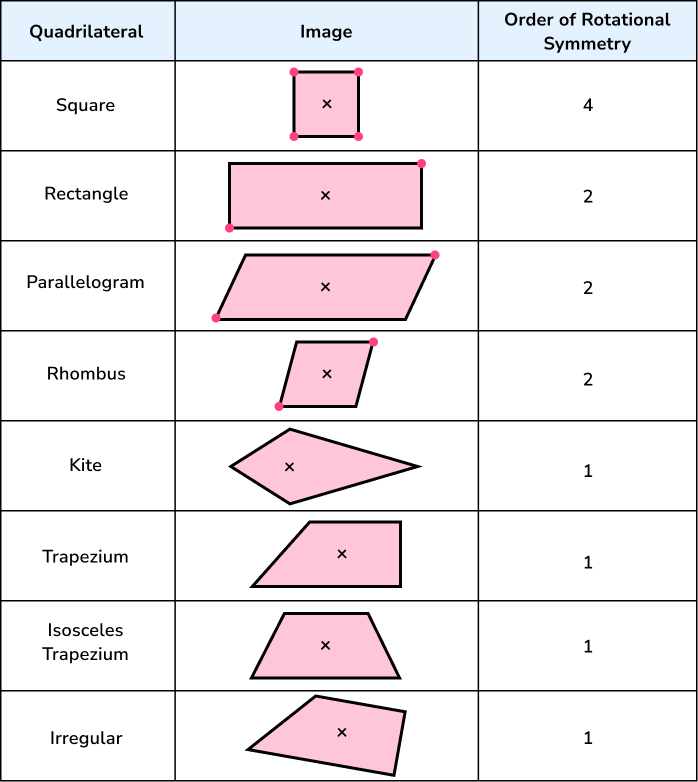
The kite is interesting because it may appear to have rotational symmetry due to it having a line of symmetry. However if the shape is rotated around its centre, it returns back to the original orientation without it fitting into itself again so the order of rotational symmetry for a kite is 1 . We can also state that any shape with rotational symmetry order 1 has “no rotational symmetry”.
This is also true for any other quadrilateral that is not a square, rectangle, parallelogram or rhombus.
Rotational symmetry in graphs
We don’t stop at shapes when we look at rotational symmetry. We can also consider rotational symmetry with different types of graphs.
E.g.
Below is the graph of the equation y=x.
Given that the line extends in both directions beyond the axes drawn above, we can use the origin as a centre of rotation. If we rotate the line 180 degrees about the origin, we will get exactly the same line. Continuing this rotation all the way through 360^o we get back to the original.
So the line y=x has an order of rotation of 2 .
Rotational symmetry in circles
A regular hexagon has an order of rotation of 6 , an octagon has an order of rotation of 8 , and a dodecagon has an order of rotation of 12 . But what about a circle?
A circle can be rotated around its centre and the shape will remain identical as the radius is the same for every point on the circumference of the circle.
This means that the order of rotational symmetry for a circle is infinite.
How to calculate the order of rotational symmetry
In order to calculate the order of rotational symmetry:
- Locate the centre of the 2D shape.
- Trace the shape onto a piece of tracing paper including the centre and north line.
- Rotate the tracing around the centre and count the number of identical occurrences.
Explain how to calculate the order of rotational symmetry

Rotational symmetry worksheet

Get your free rotational symmetry worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Rotational symmetry worksheet

Get your free rotational symmetry worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERotational symmetry examples
Example 1: the isosceles triangle
Calculate the order of rotation for the isosceles triangle below:
- Locate the centre of the 2D shape.
Draw a small x in the centre of the triangle (draw a line from each vertex to the midpoint of the line opposite).
2Trace the shape onto a piece of tracing paper including the centre and north line.
Here we use tracing paper to trace the shape including the centre of the shape and an upwards arrow (northline). The northline shows us when the shape is facing the original orientation.
3Rotate the tracing around the centre and count the number of identical occurrences
Rotating the shape around the centre, we have to turn the shape all 360^o before the traced image looks identical to the original.
The isosceles triangle has a rotational symmetry of order 1 .
Example 2: the regular hexagon
Calculate the order of rotational symmetry for a regular hexagon:
Locate the centre of the 2D shape.
Draw a small x in the centre of the hexagon (join the opposing vertices together to locate the centre):
Trace the shape onto a piece of tracing paper including the centre and north line.
As the regular hexagon has a lot of vertices, it is useful to also draw a dot in one vertex so you don’t lose sight of what the original looks like:
Rotate the tracing around the centre and count the number of identical occurrences.
Rotating the shape around the centre, there are multiple occasions when the shape is identical to the original. Below we have shown multiple stages of the rotation:
By placing a dot in each position when the shape is identical, we can count the order of rotation once the shape has been rotated 360^o around the centre.
The regular hexagon has a rotational symmetry of order 6 .
Example 3: using angles
Calculate the rotational symmetry of the octagon below.
Locate the centre of the 2D shape.
Draw a small x in the centre of the hexagon (join the opposing vertices together to locate the centre):
Trace the shape onto a piece of tracing paper including the centre and north line.
Being able to visualise the rotation without tracing is a difficult skill however for this example, as the shape is not drawn accurately, we cannot use the trace method.
Instead, we need to think about the angles in the shape and whether when we rotate the shape, that the angles would match.
If we rotate the shape through 90 degrees, we can see that the angles in the octagon look like this:
If we compare it to the original, we can see that the angles do not match and so let’s continue to rotate the shape clockwise:
Now we have rotated the shape to 180^o from the original, we can see that the size of the angles match their original position.
Rotate the tracing around the centre and count the number of identical occurrences.
If we rotated the shape a further 90 degrees, this would also not match the original and then we return the shape back to the original position.
This means that the order of rotational symmetry for this octagon is 2 .
Top tip: divide the angle at the centre by the number of sides in the shape. This angle can be used to rotate the shape around e.g. a hexagon can be rotated by an angle of 60^o clockwise six times to complete a full turn, a rectangle can be rotated 90^o clockwise four times to complete a full turn.
Example 4: angle facts
The shape ABCD has two pairs of parallel sides. Use angle facts to calculate the order of rotation for the shape ABCD .
Locate the centre of the 2D shape.
To find the centre of the shape, join the diagonals together. Here we have:
Next we need to calculate all of the interior angles of the shape and use them to calculate the order of rotation:
BAD = 180 - 55 = 125^o (co-interior angles total 180^o )
BCD = 180 - 55 = 125^o (angles on a straight line total 180^o )
ABC = 180 - 55 = 125^o (co-interior angles total 180^o )
We now have the following information:
Trace the shape onto a piece of tracing paper including the centre and north line.
Again, we are going to try visualising the rotation without tracing paper. As the shape is a quadrilateral, we will visualise turning the object through four 90 degree turns in a clockwise direction and see if the angles match.
By rotating the shape 90^o clockwise, we get a shape that is not exactly like the original.
Continuing this by another 90 degree rotation, we get:
Rotate the tracing around the centre and count the number of identical occurrences.
If we rotated the shape a further 90 degrees, this would also not match the original and then we return the shape back to the original position.
The order of rotational symmetry for the shape ABCD (which is a parallelogram) is 2.
Example 5: cubic graph
Calculate the order of rotational symmetry for the cubic graph y=x^3+2 around the centre (0,2) .
Locate the centre of the 2D shape.
We know the centre (0,2) so let us draw it onto the graph:
Trace the shape onto a piece of tracing paper including the centre and north line.
As the shape is now a graph, sketch the graph onto a piece of tracing paper. You do not need to include the axes as it is the graph that is important.
Rotate the tracing around the centre and count the number of identical occurrences.
If we turn the tracing 180^o around the point (0,2) we get a match with the original. This is the only occurrence along with the original and so the order of rotation for the cubic graph y=x^3+2 around the point (0,2) is 2 .
Example 6: sine graph
Calculate the order of rotational symmetry for the graph y=sin(\theta) around the origin.
Locate the centre of the 2D shape.
The centre of rotation is given as the origin and so let us highlight this point on the graph:
Trace the shape onto a piece of tracing paper including the centre and north line.
Rotate the tracing around the centre and count the number of identical occurrences.
Here we can only get an exact copy of the original image by rotating the tracing paper around the origin once excluding the original image.
The order of rotational symmetry for the graph of y=sin(\theta) is 2.
Common misconceptions
- Lines of symmetry
Lines of symmetry are mixed up with rotational symmetry. A line of symmetry divides the shape equally into two symmetrical pieces. A rotational symmetry is the number of times a shape fits into itself when rotated around its centre.
- Rotational symmetry of order \pmb{0}
A shape that has an order of rotational symmetry of 1 can also be said to have an order of 0 , but 1 or “no rotational symmetry” are better descriptions.
- The number of sides = the order of rotational symmetry
Although this is true for regular shapes, this is not true for all shapes.
Related lessons
Rotational symmetry is part of our series of lessons to support revision on symmetry. You may find it helpful to start with the main symmetry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Practice rotational symmetry questions
1. Calculate the order of rotational symmetry for the kite below.




Labelling one corner and the centre, if you rotate the polygon around the centre, the kite rotates 360^o before it looks like the original so it has no rotational symmetry or order 1.
2. Calculate the rotational symmetry for this regular pentagon.




Labelling one corner and the centre, if you rotate the polygon around the centre, the pentagon rotates 72^o before it looks like the original, this can be repeated 4 more times, 5 in total so it has rotational symmetry order 5.
3. What is the order of rotational symmetry for the dodecagon below?




Labelling one corner and the centre, if you rotate the polygon around the centre, the polygon can rotate 90^o before it looks like the original.
Placing a dot for each time the polygon fits (a further 3 rotations of 90^o ) so it has a rotational symmetry of 4 .
4. Calculate the order of rotational symmetry for the following shape ABCDEF:




All the interior angles are equal to 120^o and all sides are equal length
5. State the order of rotational symmetry for the graph y=4x-2 around the point (0,-2).




Rotating the graph 180^o around the point (0,-2) , we get an identical image of the original.
A further rotation of 180^o returns the shape back to the original and so it has an order of rotation of 2.
6. Calculate the order of rotational symmetry for the graph of y=cos(x) around the centre (0,0).




When rotated 180^o , this is the result. This is not identical to the original.
Rotational symmetry GCSE questions
1. ABC is a triangle. By finding the value for x , show that the triangle has an order of rotational symmetry of 0.
(4 marks)
5x-30+4x+20+6x-35=180
(1)
15x-45=180 so x=15^o
(1)
5\times15-30=45^o, \; 4\times15+20=80^o and 6\times15-35=55^o
(1)
As all the angles aren’t equal, the shape has no rotational symmetry or order 1.
(1)
2.
(a) Below are three coordinates plotted on a set of axes.
State the location of the other coordinate that will generate a quadrilateral that has a rotational symmetry of 2 and the name of the quadrilateral.
(b) What is the order of rotational symmetry for the shape if the fourth vertex of the quadrilateral was plotted at (5,0) ? State the name of the quadrilateral.
(4 marks)
(a)
(1,0)
(1)
Parallelogram
(1)
(b)
Order of rotational symmetry =0 or 1
(1)
(Isosceles) trapezium
(1)
3. Complete the table to show whether the order of rotational symmetry for each quadrilateral is Always, Sometimes, or Never equal to 0.
Give a reason for each answer.
| Quadrilateral | Always, Sometimes, Never | Reason |
| Square | ||
| Rectangle | ||
| Parallelogram | ||
| Rhombus | ||
| Kite | ||
| Isosceles | ||
| Trapezium | ||
| Arrowhead |
(5 marks)
| Quadrilateral | Always, Sometimes, Never | Reason | Mark |
| Square | Never | Always order 4 | (1) |
| Rectangle | Never | Always order 2 | |
| Parallelogram | Never | Always order 2 | |
| Rhombus | Never | Always order 2 | |
| Kite | Sometimes | A kite can be a rhombus | (1) |
| Isosceles | Sometimes | An isosceles trapezium can be a rectangle or a square | (1) |
| Trapezium | Sometimes | A trapezium can be a parallelogram, rectangle, square or rhombus | (1) |
| Arrowhead | Always | Always order 0 or 1 | (1) |
Learning checklist
You have now learned how to
- Describe, sketch and draw using conventional terms and notations: points, lines, parallel lines, perpendicular lines, right angles, regular polygons, and other polygons that are reflectively and rotationally symmetric
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.