GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Algebraic expressions Maths formulas Area of a quadrilateral Rearranging equations

This topic is relevant for:

GCSE Maths Geometry and Measure Area

Area Of A Right Angled Triangle

Area of a Right Angled Triangle

Here we will learn about the area of a right angled triangle including how to find the area of a right angled triangle with given lengths and how to calculate those lengths if they are not given.

There are also area of a triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a right angled triangle?

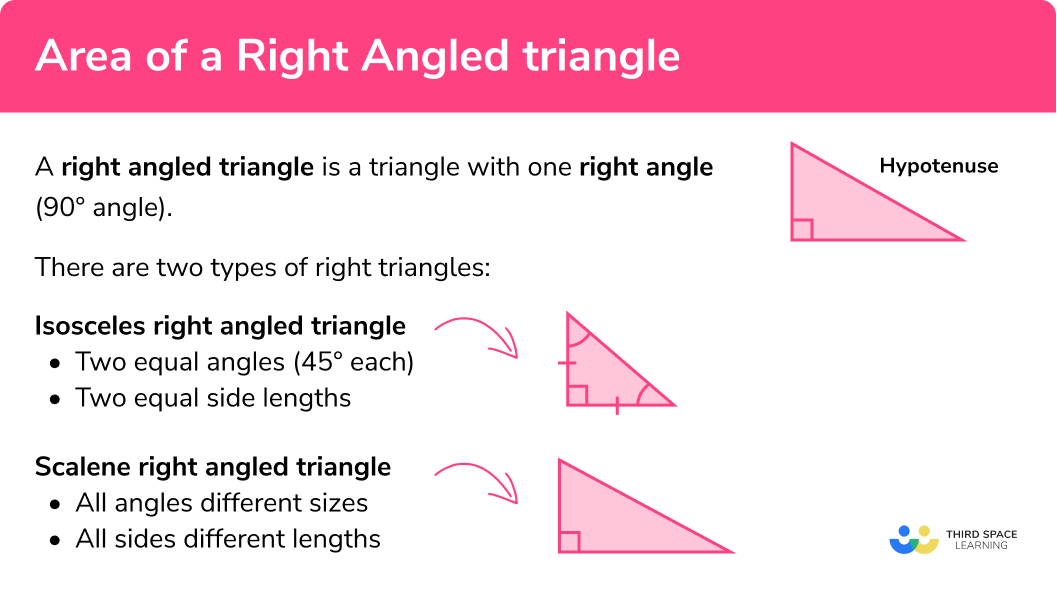
A right angled triangle is a triangle with one right angle (90° angle). The little square in the corner tells us it is a right angled triangle.

There are two types of right triangles:

Isosceles right angled triangle

-two equal angles (45° each)

-two equal side lengths

Scalene right angled triangle

-all angles different sizes

-all sides different lengths

The relationship between the angles and side lengths of the triangle form the basis of the trigonometric functions sine, cosine and tangent.

Step by step guide: Trigonometry

The side of the triangle opposite the right angle is the longest side of the triangle and is referred to as the hypotenuse.

Step by step guide: Hypotenuse (coming soon)

Right triangles are also used in the Pythagorean Theorem:

\[a^{2}+b^{2}=c^{2}\]

Step by step guide: Pythagoras’ Theorem (coming soon)

What is a right angled triangle?

How to name a triangle

We can identify a triangle by putting a capital letter on each vertex (corner).

We can then refer to each of the sides of the triangle by using two letters to describe where the line starts and ends.

We can refer to the entire triangle by using all three letters.

E.g.

Name of sides:
side AB, side AC, side BC

Name of triangle:
triangle ABC

Area of a Right Angled triangle labelled triangle

How do we find the area of a triangle?

In order to find the area of a triangle, we need to start with the area of a rectangle.

To find the area of a rectangle you must multiply adjacent sides together.

The area of the rectangle below would be calculated by multiplying the base x height
( $b$ x $h$ ).

Area of a Right Angled triangle rectangle

We can split a rectangle into 2 congruent (identical) right angled triangles.

Area of a right angled triangle congruent triangles

So the area of each of the right triangles is exactly half the area of the rectangle.

Area of a right angled triangle formula

\[\text { Area of a triangle }=\frac{\text { base } \times \text { height }}{2}\]

base and height of a right angled triangle labelled

This can be shortened to

\[A=\frac{1}{2} b h\]

where b is the base length and h is the height of the triangle.

Your final answer must be given in units² (e.g. cm², m², mm²).

How to find the area of a right angled triangle

In order to find the area of a right angled triangle:

1Identify the height and base length of your triangle (you might need to calculate these values)

2Write the formula

\[A=\frac{1}{2} b h\]

3Substitute the values for base and height

4Calculate

How to find the area of a right angled triangle

Area Of A Triangle Worksheet

Get your free area of a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions on area of a right angled triangle.

DOWNLOAD NOW

Area Of A Triangle Worksheet

Get your free area of a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions on area of a right angled triangle.

DOWNLOAD NOW

Related lessons on area

Area of a right angled triangle is part of our series of lessons to support revision on area. You may find it helpful to start with the main area lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Area of right angled triangle examples

Example 1: given base length and height

Find the area of the triangle below:

Area of a right angled triangle example 1

Identify the height and base length of the triangle

Area of a right angled triangle example 1 labelled sides

h = 7cm

b = 8cm

2Write down the formula

\[A=\frac{1}{2} b h\]

3Substitute the values for the base and height

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(8)(7) \end{aligned}\]

4Calculate

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(8)(7)\\ &=28cm^2 \end{aligned}\]

Remember: Your final answer must be in units squared.

Example 2: given base length and height

Find the area of the triangle below:

Area of a right angled triangle example 2

Identify the height and base length of the triangle

Area of a right angled triangle example 2 labelled sides

h = 200cm

b = 6m

Note: You have 2 different units here. You must convert them to a common unit 200cm = 2m.

h = 2m

b = 6m

Write down the formula

\[A=\frac{1}{2} b h\]

Substitute the values for the base and height

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(6)(2) \end{aligned}\]

Calculate

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(6)(2)\\ &=6m^2 \end{aligned}\]

Remember: Your final answer must be in units squared.

Example 3: missing height

Find the area of triangle ABC below:

Area of a right angled triangle example 3

Identify the height and base length of the triangle

Area of a right angled triangle example 3 labelled base and height

b = 5cm

In this question we are given the length of the hypotenuse which is 13cm. We need to calculate the height using Pythagoras’ Theorem.

Area of a right angled triangle example 3 using pythagoras

\[\begin{array}{l} h^{2}=13^{2}-5^{2} \\ h^{2}=169-25 \\ h^{2}=144 \\ h=\sqrt{144} \\ h=12 \mathrm{~cm} \end{array}\]

h = 12cm

Write down the formula

\[A=\frac{1}{2} b h\]

Substitute the values for the base and height

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(5)(12) \end{aligned}\]

Calculate

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(5)(12)\\ &=30cm^2 \end{aligned}\]

Remember: Your final answer must be in units squared.

Example 4: missing length given an angle

Below is a right angled triangle with height of $4 \, cm$ and an angle of $35^{\circ}.$

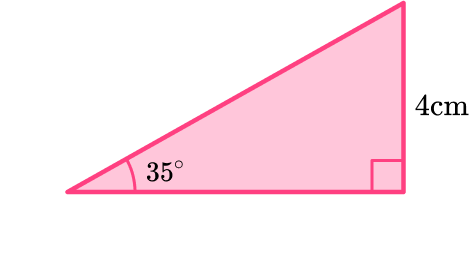
Find the area of the triangle.

Identify the height and base length of your triangle. (You might need to calculate these values)

The height of $4 \, cm$ is given and an angle of $35^{\circ}$ so we need to use SOHCAHTOA to find the base.

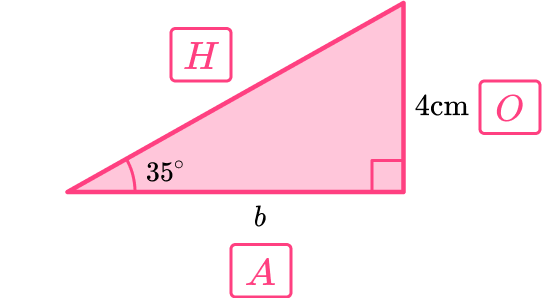
$\tan \left( 35 \right)=\frac{4}{b}$

So,

$\begin{aligned} b&=\frac{4}{\tan \left( 35 \right)} \\\\ & =5.71 \,cm \end{aligned}$

Write down the formula

\[A=\frac{1}{2} b h\]

Substitute the values for the base and height

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(5.71)(4) \end{aligned}\]

Calculate

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(5.71)(4)\\\\ &=11.43 \, cm^2 \end{aligned}\]

Example 5: compound shape

Below is the floor plan for a new deck that needs to be painted. One can of paint costs £12 and covers an area of 2.5m². How much would it cost to paint the entire deck?

Area of a right angled triangle example 4

Identify the height and base length of the triangle

Area of a right angled triangle example 4 base length

Split the plan into 2 shapes. You have a rectangle and a right angled triangle.

For the triangle:

b = 2.5m h = 3.5m

Write down the formula

\[A=\frac{1}{2} b h\]

Substitute the values for the base and height

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(2.5)(3.5) \end{aligned}\]

Calculate

\[\begin{aligned} A &=\frac{1}{2} b h \\ &=\frac{1}{2}(2.5)(3.5)\\ &=4.375m^2 \end{aligned}\]

Now you must find the area of the rectangle.

\[\begin{aligned} \text { Area of a rectangle }&=l \times w \\ &=2.5 \times 3 \\ &=7.5 m^{2} \\ \end{aligned}\]

Total Area = 4.375 + 7.5 = 11.875 m²

Now we need to divide 11.875 by 2.5 since one can of paint only covers an area of 2.5m²:

11.875 ÷ 2.5 = 4.75

This means you have to buy 5 cans of paint as we can only buy whole cans of paint.

Now to work out the cost: 5 cans of paint x £12 = £60

The total cost to paint the deck is £60.

How to find a missing side length given the area

Sometimes a question might give you the area and ask you to work out the height or missing length. In order to do this you must rearrange the formula.

To find a missing length given the area:

1Rearrange the formula

2Substitute in the values you know

3Calculate

Example 6: calculating base length

Triangle $XYZ$ is a right triangle with an area of 15cm². The height of the triangle is 5cm. Find the base length of the triangle.

Rearrange the formula

\[A = \frac{1}{2}bh\]

to make b the subject, start by multiplying both sides of the formula by 2

\[2A = bh\]

Next we need to divide both sides of the formula by h

\[\frac{2(A)}{h}=b\]

Now substitute the given values

Area = 15

Height = 5

\[b=\frac{2(15)}{5}\]

Calculate

\[\begin{aligned} b&=\frac{2(15)}{5} \\ b&=\frac{30}{5} \\ b&=6 \mathrm{~cm} \end{aligned}\]

Common misconceptions

Identifying the correct information to use

A question may give extra information that is not needed to answer it. Carefully identify the relevant pieces of information.
E.g.
To calculate the area here we only need the base and height.

Base= 4cm,

Height = 3cm

Area=

\[\frac{3 \times 4}{2} = 6cm^{2}\]

We can ignore the value of the hypotenuse (5cm)

Units

It is common error to forget the units for area in the final answer. When calculating area, your answer must always have units squared.

Practice area of right angled triangles questions

108cm^{2}

54cm^{2}

27cm^{2}

36cm^{2}

The lengths needed for the base and the height are $9cm$ and $12cm$ , so the calculation we need to do is $\frac{1}{2} \times 9 \times 12 = 54cm^{2}$

22.5cm^{2}

45cm^{2}

2250cm^{2}

4500cm^{2}

We need to convert the units so that they are the same.

0.9m=90cm

Then the calculation needed is $\frac{1}{2} \times 90 \times 50$ = $2250cm^{2}$

2

3

24

25

We can treat the shape as a rectangle with area $3.2 \times 4.5 = 14.4m^{2}$ and a triangle with area $\frac{1}{2} \times 4.5 \times 4.5 = 10.125m^{2}$ .

This gives a total area of $14.4 + 10.125 = 24.525m^{2}$ .

By considering multiples of $9$ , we conclude that $2$ meerkats can fit into the cage.

54cm^{2}

101.82cm^{2}

72cm^{2}

50.91cm^{2}

Using Pythagoras’ Theorem to find length $AB$

AB=\sqrt{18^{2}-6^{2}}

AB=16.97\dots

The area is then given by $\frac{1}{2} \times 6 \times 16.97$ = $50.91cm^{2}$

8cm

800cm

2cm

200cm

Starting with the formula for the area of a triangle: $Area=\frac{1}{2} \times$ base $\times$ height

We substitute in the known information (convert lengths to the same units), so

$40=\frac{1}{2} \times 10 \times$ height

$40=5 \times$ height

Therefore:

height = $8cm$

Area of a right angled triangle GCSE questions

1. A logo is in the shape of a right angled triangle. It has a base length of $10cm$ and a height of $4.5cm$ . Calculate the area of the logo.

(2 marks)

Show answer

A = \frac{1}{2}\times 10 \times 4.5

(1)

A=22.5cm^{2}

(1)

2. The diagram below shows the plan of a rectangular garden:

Area of a right angled triangle GCSE lawn Q

Calculate the area of the lawn.

(3 marks)

Show answer

Area of rectangle:

5 \times 12 = 60m^{2}

(1)

Area of triangle:

\frac{1}{2} \times 3 \times 5 = 7.5m^{2}

(1)

Area of lawn:

60-7.5=52.5m^{2}

(1)

3. The area of the square and the area of the right angled triangle below are equal.

Area of a right angled triangle GCSE q2

Work out the height of the triangle.

(4 marks)

Show answer

Area of square:

6 \times 6 = 36cm^{2}

(1)

Rearrange area of triangle:

\begin{aligned} A &= \frac{1}{2} bh \\ 2A &= bh\\ h &= \frac{2A}{b} \end{aligned}

(1)

Substitute in values:

h= \frac{2 \times 36}{9}

\begin{array}{l} h= \frac{72}{9}\end{array}\begin{array}{l} h=8cm \end{array}

(1)

Learning checklist

You have now learned how to:

Apply formula to calculate and solve problems involving the area of triangles

Use Pythagoras’ Theorem to solve problems involving triangles

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.