How To Find Mass With Density And Volume

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Arithmetic How to calculate volume Units of measurement Conversion of units

This topic is relevant for:

GCSE Maths Ratio and Proportion Compound Measures Mass Density Volume

How To Find Mass With Density And Volume

Here we will learn about how to find mass with density and volume, including using the density formula.

There are also how to find mass with density and volume worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is mass (with density and volume)?

We can calculate how to find mass with density and volume by using the mass formula,

M=D\times{V}

where $\textbf{M}$ represents mass, $\textbf{V}$ represents volume and $\textbf{D}$ represents density of an object.

This is the density equation or density formula, although to calculate the mass, we have rearranged the formula to make the mass the subject. We can also represent this using the density mass volume triangle,

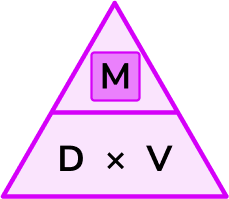
How to find mass with density and volume image 1

What is mass (with density and volume)?

● Mass

The mass of an object is the amount of matter there is in an object.

The standard SI units of mass is kilograms $(kg)$ but we can also use other metric units such as grams, milligrams or tonnes. The following table shows the conversion of $1kg$ to these other units.

Unit	$\bf{1kg \ =}$
Tonne $(t)$	$0.001 \ t$
Grams $(g)$	$1000 \ g$
Milligrams $(mg)$	$1,000,000 \ mg$

Imperial units include stones $(st),$ pounds $(lb),$ ounces $(oz)$ and imperial tons $(ton).$

The imperial ton is not the same as the metric tonne, as $1 \ ton = 1.01605 \ t.$

Mass calculator

The mass of an object can be calculated if we know the density and volume of the object.

Mass is directly proportional to the volume of an object with a constant density; the heavier the mass, the larger the volume when the density remains the same.

This means that we can state $M\propto{V}$ or $M=kV$ where the constant of proportionality, $k,$ represents the density of the object.

● Volume

The volume of an object is how much space an object or substance takes up. The SI unit for volume is cubic metres written as $m^3.$ Other volumetrics we should be aware of are the cubic centimetre $(cm^{3})$ and the cubic millimetre $(mm^{3}).$

The volume of a liquid is referred to as its capacity where $1 \ cm^3 = 1 \ ml \ (1$ millilitre), and hence $1000 \ cm^3 = 1L (1$ litre).

Volume calculator

The volume of a substance can be calculated if we know the density and mass of the object.

Volume is inversely proportional to the density of an object with a constant mass; the greater the volume, the lower the density of the object or substance with a constant mass.

This means that, for volume $V$ and density $D,$ we can state $V\propto\frac{1}{D}$ or $V=\frac{k}{D}$ where the constant of proportionality, $k,$ represents the mass of the object.

● Density

Density is another physical property of an object or substance. The density of a material is a compound measure that relates how much matter there is in the substance per unit volume.

For example, a sponge has a higher density when it is squeezed as its volume has decreased, but the mass has not changed. Conversely, when the sponge has been released, it has a lower density as the volume has increased but the mass has stayed the same.

Below is a table describing some density measurements.

Unit	Description
$g/cm^3$	Grams per cubic centimetre
$kg/m^3$	Kilograms per cubic metre
$mg/ml$	Milligrams per millilitre

Notice that the first unit of each density unit is a mass (grams, kilograms, milligrams) and the divisor is a volume measurement (cubic centimetres, cubic metres, and millilitres).

Remember: $1cm^3 = 1 \ ml.$

At $4^{o}C,$ the density of water is $1000 \ kg/m^{3},$ which is the same as $1g/cm^{3}.$

Density calculator

The density of a substance can be calculated if we know the volume and mass of the object.

Density is inversely proportional to the volume of an object with a constant mass; the greater the density, the lower the volume of the object or substance with a constant mass.

This means that, for density $D$ and volume $V,$ we can state $D\propto\frac{1}{V}$ or $D=\frac{k}{V}$ where the constant of proportionality, $k,$ represents the mass of the object.

How to find mass with density and volume

In order to find mass with density and volume:

Write the formula with the correct subject.
Substitute known values into the formula and do the calculation.
Write down the solution including the units.

Explain how to find mass with density and volume

How to find mass with density and volume worksheet

Get your free how to find mass with density and volume worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

How to find mass with density and volume worksheet

Get your free how to find mass with density and volume worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on compound measures

How to find mass with density and volume is part of our series of lessons to support revision on compound measures. You may find it helpful to start with the main compound measures lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

How to find mass with density and volume examples

Example 1: calculate mass in grams

Find the mass of an object with volume $300 \ cm^{3}$ and density $5 \ g/cm^{3}.$ Give your answer in grams.

Write the formula with the correct subject.

M=DV

2Substitute known values into the formula and do the calculation.

\text{Mass}=\text{density}\times \text{volume}=5\times 300=1500

3Write down the solution including the units.

Mass $= 1500g$

Example 2: calculate mass in grams

Find the mass of an object with volume $450 \ cm^3$ and density of the material is $7.2 \ g/cm^{3}.$ Give your answer in grams.

Write the formula with the correct subject.

M={D}\times{V}

Substitute known values into the formula and do the calculation.

M={D}\times{V}=7.2\times{450}=3240

Write down the solution including the units.

Mass $= 3240g$

Example 3: calculate mass in kilograms

Find the mass of a solid object with volume $4 \ m^3$ and density of the material is $7500 \ kg/m^{3}.$ Give your answer in tonnes.

Write the formula with the correct subject.

M={D}\times{V}

Substitute known values into the formula and do the calculation.

M={D}\times{V}={7500}\times{4}=30,000

Write down the solution including the units.

As $1 \ tonne = 1000 \ kg,$ we need to divide $30,000$ by $1000$ to convert the units from kilograms to tonnes.

$30000\div{1000}=30$

Mass $= 30 \ t$

Example 4: calculate mass when units need converting

Find the mass of an object with volume $950 \ cm^3$ and density of the material is $18.2 \ g/cm^{3}.$ Write your answer in kilograms.

Write the formula with the correct subject.

M={D}\times{V}

Substitute known values into the formula and do the calculation.

M={D}\times{V}={18.2}\times{950}=17290

Write down the solution including the units.

The mass is currently in grams, and we need to convert it to kilograms.

We do this by dividing the mass by $1000$ as $1000g = 1 \ kg.$

$17290\div{1000}=17.29$

Mass $= 17.29 \ kg$

Example 5: calculate mass when units need converting

Find the mass of an object with volume $0.000875 \ m^3$ and density $15.3 \ g/cm^{3}.$ Write your answer in kilograms.

Write the formula with the correct subject.

M={D}\times{V}

Substitute known values into the formula and do the calculation.

As the volume unit is in $m^3$ and the density unit is in $g/cm^3$ we need to convert the volume to $cm^{3}.$ As $1m^3 = 1,000,000 \ cm^{3}$ , we need to multiply the volume by $1000000 \ (= 1$ million, or $10^{6})$ first, then substitute the values into the formula.

$V=0.000875\times{1000000}=875cm^{3}$

Now $V=875 \ cm^3$ and $D=15.3 \ g/cm^3$ and so

$M={D}\times{V}={15.3}\times{875}=13387.5$ .

Write down the solution including the units.

Mass $= 13.3875 \ kg$

Example 6: calculate mass when units in standard form

Find the mass of an object with volume $(2 \times 10^{6} ) \ cm^3$ and density of the material is $3 100 \ kg/m^{3}.$ Write your answer in tonnes.

Write the formula with the correct subject.

M={D}\times{V}

Substitute known values into the formula and do the calculation.

The volume is currently in cubic centimetres, which we can convert to cubic metres by dividing by $1000000.$

$(2\times{10}^{6})\div{1000000}=2\times{10^{6}}\div{10^{6}}=2$

Now $V=2m^3$ and so

$M={D}\times{V}={3100}\times{2}=6200$ .

Write down the solution including the units.

The answer is required in tonnes and so dividing $6200$ by $1000,$ we have

Mass $= 6.2 \ t.$

Common misconceptions

Incorrect orientation of the formula

It is common to write the relationship between density, mass, and volume incorrectly. A useful way to remember the correct orientation is using the units for density. As density is a mass, divided by a volume, if we multiply the density by a volume, the units we are left with are a mass.

Units of measure

We tend to use metric units for mass, density and volume. We need to be able to convert between metric units such as knowing there are $100 \ cm$ in $1$ metre. Occasionally you might come across other types of units such as imperial units like the cubic foot.

Converting units (linear)

You may have worked out grams, but the answer needs to be in kilograms.

Remember that $1 \ kg = 1000 \ g.$

Remember that $1 \ tonne = 1000 \ kg.$

Converting units (volume)

A volume uses cubic units such as $m^3$ and $cm^{3},$ or capacity units such as $ml$ and $L.$ The conversion for cubic units is the cube of the scale factor. For example, a cube with a side length of $1m$ has a volume of $1m^{3}.$

The same cube has a side length of $100 \ cm,$ and so the volume of the cube is $100^3 = 1,000,000 \ cm^{3}.$ This means that $1 \ m^{3}=1,000,000 \ cm^3$ and so if we convert cubic metres to cubic centimetres, we need to multiply the volume by $1,000,000.$

Practice how to find mass with density and volume questions

400 \ g

360 \ g

40 \ g

36 \ g

\text{Mass}=\text{density}\times \text{volume}=3\times 120=360

620 \ g

660 \ g

640 \ g

680 \ g

\text{Mass}=\text{density}\times \text{volume}=4\times 170=680

1.8 \ kg

0.18 \ t

18 \ t

1.8 \ t

\begin{aligned} &\text{Mass}=\text{density}\times \text{volume}=6000\times{3}=18 000 \\\\ &18000\div{1000}=18 \ t \end{aligned}

10 \ 660 \ g

1 \ 066 \ g

1.066 \ kg

10.66 \ kg

\begin{aligned} &0.00082 \ m^3 = 820 \ cm^3 \\\\ &\text{Mass}=\text{density}\times \text{volume}=13\times 820=10 660 \end{aligned}

As $1 \ kg = 1000 \ g,$ we need to divide by $1000$ to convert to kilograms.

10 \ 660 \div 1000 = 10.66 \ kg

12150 \ tonnes

121.5 \ tonnes

0.1215 \ tonnes

12.15 \ tonnes

\text{Mass}=\text{density}\times \text{volume}=2700\times 4.5=12 150

We need to divide by $1000$ to convert to tonnes.

12150\div{1000}=12.15 \ tonnes

37.17 \ tonnes

371.7 \ tonnes

371700000 \ g

0.003717 \ tonnes

\begin{aligned} &5.9 \ m^{3}=5900000 \ cm^{3} \\\\ &M=D\times{V}=63\times{5900000}=371700000 \\\\ &1 \ t=1000 \ kg=1000000 \ g \\\\ &371700000\div{1000000}=371.7 \ t \end{aligned}

How to find mass with density and volume GCSE questions

1. A block of wood had density $1.6 \ g/cm^3$ and a volume of $300 \ cm^{3}.$

Calculate the mass of the block of wood.

(2 marks)

Show answer

1.6\times \ 300

(1)

480

(1)

2. A platinum bar has a density of $21.4 \ g/cm^3$ and a volume of $480 \ cm^{3}.$

A gold bar has a density of $19.32 \ g/cm^3$ and a volume of $530 \ cm^{3}.$

Which bar has the greater mass?

(3 marks)

Show answer

21.4\times 480=10272 \ g

(1)

19.32\times 530=10239.6 \ g

(1)

Platinum

(1)

3. Here is a block of iron.

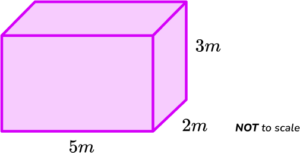
How to find mass with density and volume gcse question 3

It measures $5 \ m$ by $2 \ m$ by $3 \ m.$

The density of iron is $7800 \ kg/m^{3}.$

A crane has a maximum load weight of $2.4 \times 10^{6} \ N.$

Given that $w=mg$ where $w$ is the weight in Newtons, $g=9.807 \ m/s^{2},$ and $m$ is the mass in kilograms, can the crane pick up the block of iron?

Show all your working.

(5 marks)

Show answer

5\times 2\times 3=30 \ m^3

(1)

7800\times 30=234 000 / kg

(1)

234000\times{9.807}=2294838

(1)

2294838=2.294838\times{10}^{6} \ N\textbf{ or }2.4\times{10}^{6}=2400000 \ N

(1)

Yes

(1)

Learning checklist

You have now learned how to:

Use compound units such as density to solve problems

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.