One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Converting metric units of area and volume Volume of prisms Volume of cylinders Volume of a coneThis topic is relevant for:

Flow Rate
Here we will learn about flow rate, including how to calculate it and how to use it to solve problems involving volume and capacity.
There are also flow rate worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is flow rate?
Flow rate is the term used to describe the rate at which a fluid or substance flows into or out of an object.
To calculate flow rate we can use information about the change in capacity (or volume) of the substance and the amount of time taken for that change to occur.
\text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}}It is important in GCSE mathematics questions to look at the unit of time being used and whether the question is referring to a volume of fluid. The flow rate could be given as a compound measure such as depth per second or volume per minute.
Typical GCSE mathematics questions involve having to find the time taken for a shape to be filled or for the depth of a container to reach a specific height.
For example,
A tap is used to fill a container in the shape of a cuboid measuring 1.5 \ m by 2 \ m by 0.4 \ m. The tap releases water at a flow rate of 5 litres per minute.
Find the time taken for the container to be filled.
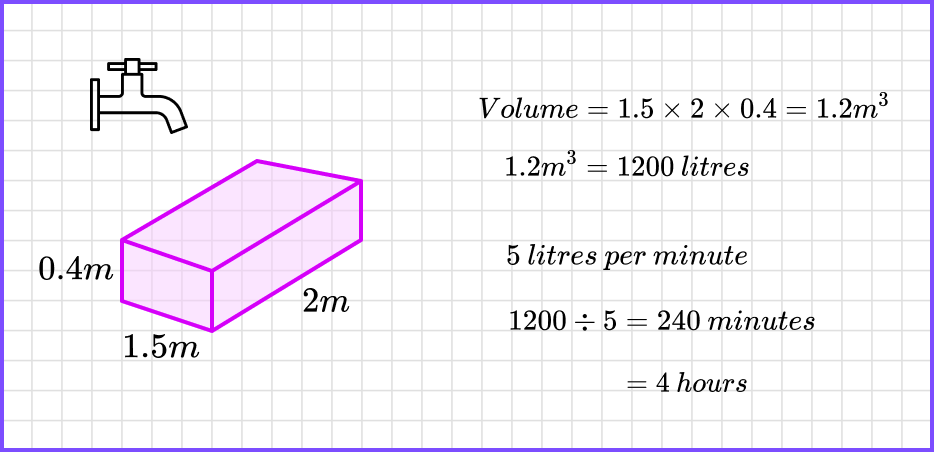
What is flow rate?

Rate of output
We measure flow rate in metres cubed per second (m^3/s), or in litres per second (l/s). Litres are the more common measures used for liquid volume. We also need to remember the conversion factor 1m^{3} = 1000 litres. The rate of output is the amount of time it takes to discharge an amount of liquid.
For example,
The diagram shows a swimming pool.
The swimming pool is empty and is then filled with water at a constant rate of 25 litres per minute.
Work out how long it will take for the swimming pool to be completely full of water. Give your answer in hours.
We need to find the volume of the swimming pool, so we can find out the amount of water it can hold.
Volume of the swimming pool = 1.8m^{3}
Using the conversion factor 1m^{3} = 1000 Litres, the swimming pool holds 1800 litres of water.
If the pool is filled with water at a constant rate of 25 litres per minute, this is our rate of output.
1800 ÷ 25 = 72 minutes
It takes 72 minutes to fill the pool.
We are asked to give our answer in hours, 72 minutes = 1 hour 12 minutes or 1.2 hours.
How to solve flow rate problems
In order to solve flow rate problems:
- Use information provided to calculate the flow rate.
\text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}} - Use information provided to calculate volume that will be changing.
- Calculate the required value.
Explain how to solve flow rate problems

Flow rate worksheet

Get your free flow rate worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Flow rate worksheet

Get your free flow rate worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on compound measures
Flow rate is part of our series of lessons to support revision on compound measures. You may find it helpful to start with the main compound measures lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Flow rate examples
Example 1: finding the time taken to fill a container
Water flowing from a hose pipe fills a 10 litre bucket in 2 minutes. Find the time it would take to fill a container in the shape of a cuboid measuring 2 metres by 1 metre by 50 \ cm.
- Use information provided to calculate the flow rate.
The flow rate of the water is 10 \div 2 = 5 litres per minute.
2Use information provided to calculate volume that will be changing.
Volume of the cuboid = 2 \times 1 \times 0.5 = 1 m^{3}.
3Calculate the required value.
We can work out the time by dividing the volume by the flow rate.
\text{Time taken}=\frac{\text{volume}}{\text{flow rate}}We need to convert the volume so that the units fit in with the volume.
1 \ m^{3} = 1000 \ litres 1000\div 5=200So the time will be 200 minutes or 3 hours 20 minutes.
Example 2: finding the volume after an allotted time
A tap has been left running. Water flows from the tap at a rate of 250 \ cm^3 \ per \ minute.
How many litres of water will come out of the tap in half an hour?
Use information provided to calculate the flow rate.
We have been given the flow rate, 250 \ cm^3 \ per \ minute.
Use information provided to calculate volume that will be changing.
Here we need to find the volume. But we have been given a time – half an hour is 30 minutes.
Calculate the required value.
We need to adapt the flow rate formula,
\text{Volume}=\text{flow rate}\times \text{time taken}
So,
\begin{aligned} \text{Volume}&=\text{flow rate}\times \text{time taken}\\\\ \text{Volume}&= 250\times 30 \\\\ \text{Volume}&=7500 cm^3 \end{aligned}
Example 3: finding the height after an allotted time
Water flowing from a tap fills a 500 \ ml jug in 80 seconds.
The same tap will be used to fill this cylindrical container, with a radius of 12 \ cm.
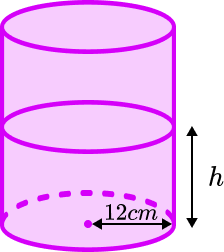
Find the height of the water, h , after 3 minutes.
Use information provided to calculate the flow rate.
We will be finding the volume of the cylinder in cm^{3}, so we will convert to flow rate so that the units match.
500 \ ml = 500 \ cm^3
The flow rate of the water is 500 \div 80 =6.25 \ cm^3 per second.
Use information provided to calculate volume that will be changing.
The cross-sectional area of the cylinder is a circle.
The volume of the cylinder of water will be \pi \times 12^2 \times h=144\pi h \ cm^3 .
Calculate the required value.
We need to calculate the volume.
The flow rate is in cm^3 per second, so we need to convert the time to seconds to fit.
3 minutes = 180 seconds
We need to adapt the flow rate formula,
\text{Volume}=\text{flow rate}\times \text{time taken}
So,
\begin{aligned} \text{Volume}&=\text{flow rate}\times \text{time taken}\\\\ 144 \pi h &= 6.25\times 180 \\\\ h &= \frac{6.25\times 180}{144 \pi}\\\\ h&=2.4867...\\\\ h&=2.49 \ \text {cm} \ \text{(2 dp)} \end{aligned}
Example 4: finding the time taken for a container to empty
A container full of water is found to have a leak.
The container is in the shape of a trapezium prism shown below and water is leaking from point P.
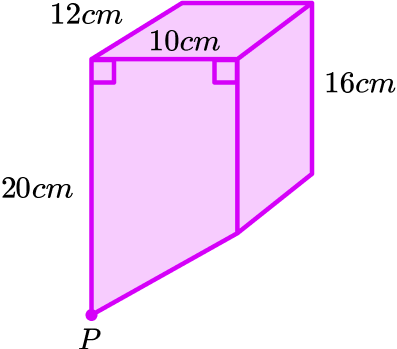
4 minutes after being completely full, the water level in the container has dropped by 2 \ cm.
Assuming the flow rate of the leak is constant, find the total time for all the water to leak out of the container.
Use information provided to calculate the flow rate.
As the shape of the container is a trapezium, use the volume of the water lost to find the flow rate.
The volume lost = 10 \times 12 \times 2 = 240 \ cm^{3}.
The flow rate of the water is 240 \div 4 = 60 \ cm^3 per minute.
Use information provided to calculate volume that will be changing.
The cross-sectional area of the container is a trapezium.
The volume of the trapezium = \frac{20 + 16}{2} \times 10 \times 12=2160 \ cm^{3}.
This is the volume of the full tank.
Calculate the required value.
2160 \div 60 = 36 minutes
The tank would take a total of 36 minutes to empty.
Common misconceptions
- Forgetting to convert units of volume or time
It is important to ensure the correct units are being used throughout a problem. If the flow rate is given in cm^3 per minute it is important to make sure all measurements are converted to centimetres and that time is given in minutes.
Practice flow rate questions
1. A tap can fill a 500 \ ml jug in 8 seconds. Calculate the flow rate, giving the units.
0.0625 \ ml per second

62.5 \ ml per second

0.016 \ ml per second

62.5 seconds per ml

Use the formula,
\begin{aligned} \text{Flow rate}&=\frac{\text{change in volume}}{\text{time taken}} \\\\ \text{Flow rate}&=\frac{500}{8}=62.5 \end{aligned}
2. A tap produces a flow rate of 30 \ cm^3 per second. How long will it take to fill a container with a volume of 195 \ cm^{3}.
6.5 seconds

5850 seconds

0.154 seconds (to 3 dp)

195 seconds

Use the formula,
\text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}}
and rearrange to find the time taken.
\text{Time taken}=\frac{\text{change in volume}}{\text{flow rate}}=\frac{195}{30}=6.5
3. A hose pipe is used to fill a water butt. Water flows at a rate of 3.5 litres per minute and fills the water butt in 12 minutes and 52 seconds. Calculate the volume of the water butt to the nearest litre.
51 litres

44 litres

45 litres

42 litres

Convert the time to decimalised form, then use the formula
\text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}}
and rearrange to find the volume.
\text{Volume}=\text{flow rate}\times \text{time taken}=3.5\times 12\frac{52}{60}=45.0333…
The volume will be 45 litres, to the nearest litre.
4. A hose can produce a flow rate of 6 cubic metres per hour. How long would it take the same hose to fill the swimming pool below? The cross-section of the swimming pool is a trapezium. Give your answer in hours and minutes.
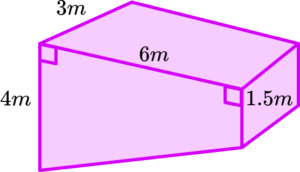
8 hours 45 minutes

9 hours

8 hours 15 minutes

8 hours 25 minutes

The volume of the swimming pool is
\text{Volume}=\frac{1}{2}\times (4+1.5)\times 6\times 3=49.5 .
Using the formula
\text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}}
we rearrange to find the time taken.
\text{Time taken}=\frac{\text{change in volume}}{\text{flow rate}}=\frac{49.5}{6}=8.25
So the time is 8.25 hours or 8 hours 15 minutes.
5. A swimming pool has dimensions shown in the diagram below. It took 19 hours 12 minutes to fill the swimming pool from a hose. Find the flow rate of the water from the hose in m^3 per hour.
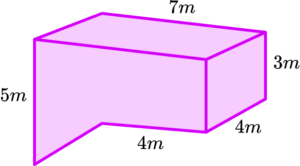
5 \ m^3 per hour

5.02 \ m^3 per hour ( 2 d.p.)

5.83 \ m^3 per hour ( 2 d.p.)

5.86 \ m^3 per hour ( 2 d.p.)

Find the volume of the swimming pool.
\text{Volume}=(7\times 3\times 4) +(\frac{1}{2}\times 2\times 3\times 4)=96
Then use the formula,
\text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}}=96\div 19\frac{12}{60}=5
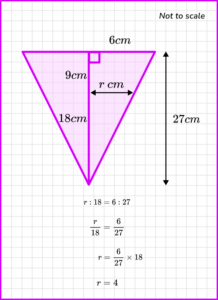
6. A container in the shape of a cone with radius 6 \ cm and height 27 \ cm , is leaking water from its apex.
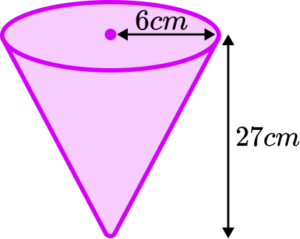
The container is originally full and after 20 minutes the depth of water has reduced by 9 \ cm. Calculate the flow rate of the leak in cm^3 per minute. Give your answer to 3 significant figures.
39.7 \ cm^3 per minute (to 3 sf)

35.8 \ cm^3 per minute (to 3 sf)

29.3 \ cm^3 per minute (to 3 sf)

24.7 \ cm^3 per minute (to 3 sf)

Use similar triangles to find the radius of the reduced cone.
Find the volume of the small cone and the large cone and then subtract the volumes to find the change in volume.
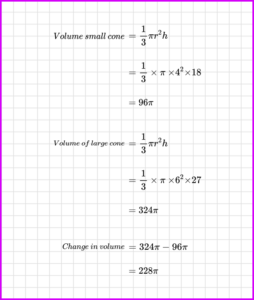
Then we can find the flow rate.

Flow rate GCSE questions
1. The diagram shows a container in the shape of the cuboid. The base of the container is a rectangle measuring 32 \ cm by 24 \ cm.
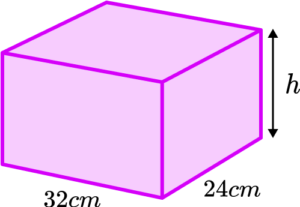
A tap produces a flow rate of 4 litres per minute.
The tap can fill the container in 4 minutes and 48 seconds.
Using the fact that 1 \ litre = 1000 \ cm^3 , find the height of the container in centimetres.
(4 marks)
(1)
4 \ litres \ per \ min = 4000 \ cm^3 \ per \ min(1)
4000\times 4.8=19200 cm^3(1)
19200\div \left( 32\times 24 \right)=25 cm(1)
2. The organiser of a fun run needs to provide 120 cups of water for competitors to drink from during a race. Each cup is a cylinder of radius 4 \ cm and height 10 \ cm as shown in the diagram.
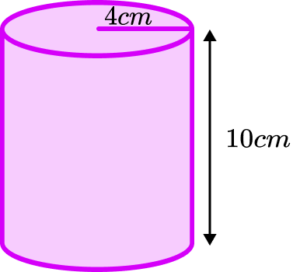
The organiser needs to fill all 120 cups with water from a tap which has a flow rate of 3.5 litres per minute. There is only 16 minutes available to get all of the cups filled.
Will the organiser get all of the cups filled in the available time? You must show your workings.
Use the fact that 1 \ litre = 1000 \ cm^{3}.
(4 marks)
Volume of 1 cup = \pi \times {{4}^{2}}\times 10=502.65… cm^3
(1)
Total volume = 502.65… \times 120= 60318.5 \ cm^3
(1)
Finding time by dividing by 3500 or equivalent = 17.23… minutes
(1)
Answer of ‘no’ with correct workings
(1)
3. The image shows a full swimming pool that needs cleaning, so will be emptied by a pump.
After 30 minutes the water level has decreased by 40 \ cm.
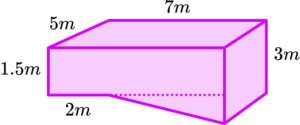
How much extra time will be required for the swimming pool to be completely empty? Give your answer in minutes.
(5 marks)
Volume of decrease = 40 \times 500 \times 700=14 \ 000 \ 000 \ cm^3
(1)
Flow rate =14 \ 000 \ 000 \ cm^3 \div 30=466 \ 666.666 … \ cm^3 \ \text{per minute}
(1)
Remaining volume
Area of cross-section =(120\times 700)+(\frac{1}{2}\times 500 \times 140)=119 \ 000 \ cm^2
(1)
Volume =119 \ 000 \times 500 = 59 \ 500 \ 000 \ cm^3
(1)
Remaining time =59 \ 500 \ 000\div 466 \ 666.6…=125.5 \ \text{minutes}
(1)
Alternatively
Volume of decrease = 0.4 \times 5 \times 7=14 \ cm^3
(1)
Flow rate =14 \ m^3 \div 30=0.466666 … \ m^3 \ \text{per minute}
(1)
Remaining volume
Area of cross-section =(1.2\times 7)+(\frac{1}{2}\times 5 \times 1.4)=11.9 \ m^2
(1)
Volume =11.9 \times 5 = 59.5 \ m^3
(1)
Remaining time =59.5\div 0.466666…=125.5 \ \text{minutes}
(1)
Learning checklist
You have now learned how to:
- Use compound measures to solve problems
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.