GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Probability scale How to calculate probability Conditional probability Systematic listing strategies Expected frequencyThis topic is relevant for:

Probability Notation
Here we will learn about probability notation, including set notation.
There are also probability notation worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is probability notation?
Probability notation is an efficient way of writing the probability of events happening or not happening.
To do this we use set notation, which is used when working with Venn diagrams.
Events are usually notated using capital letters, as well as the use of some greek letters.
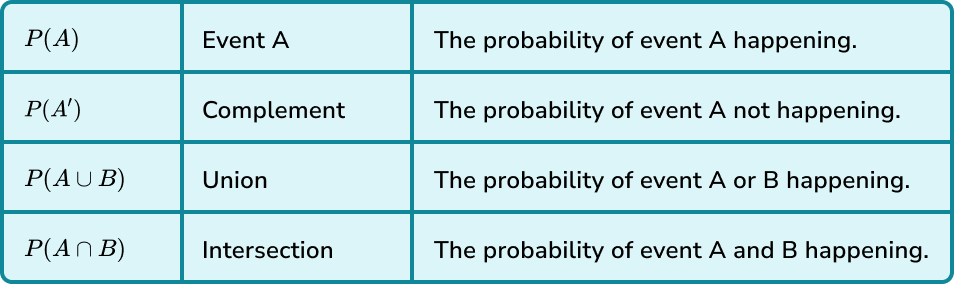
Let’s look at some examples.
If you were to roll a fair six sided dice and event A is rolling a six, a more efficient way of writing ‘what is the probability of rolling a 6’, you could write P(A) or P(6).
If you were to roll a fair six sided dice and event A is rolling a six, a more efficient way of writing ‘what is the probability of not rolling a 6’, you could write P(A’).
This links to Venn diagrams. Below are two Venn diagrams which involve two sets and show event A and anything that is not event A.
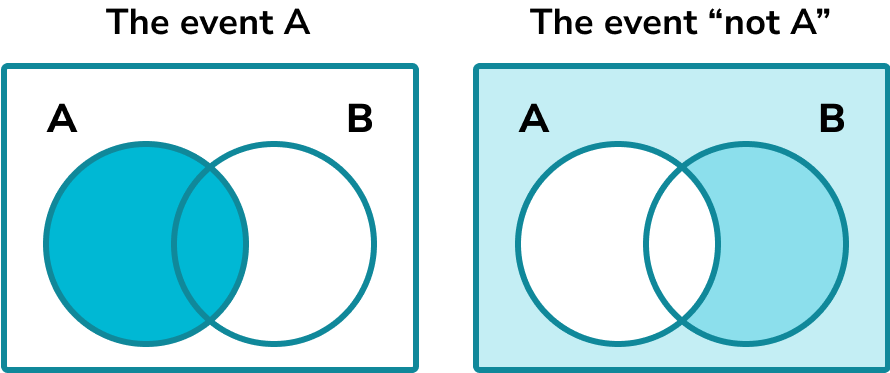
Step-by-step guide: Venn diagrams
What is probability notation?

Union
P(A \cup B) or ‘A union B’ is the chance of picking any outcome that is satisfied by event A or event B or both.
In a Venn diagram it would be presented like this.
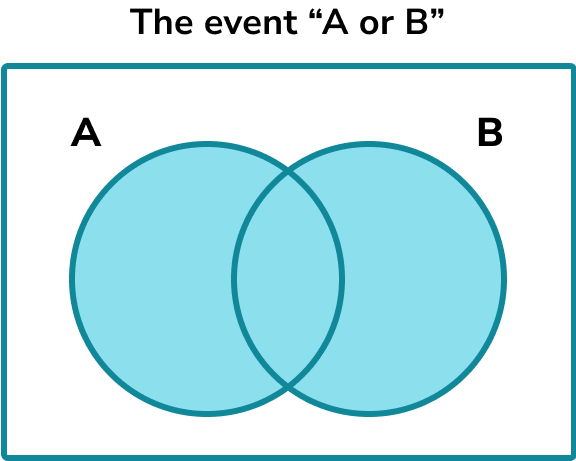
For example, \xi is the set of numbers, 1-12. \ A and B are subsets of \xi .
A = multiples of 3.
B = multiples of 4.
One of the numbers is picked at random. Find the probability P(A \cup B).
Event A are the multiples of 3 = 3, 6, 9, 12 .
Event B are the multiples of 4 = 4, 8, 12 .
The numbers 1, 2, 5, 7, 10 and 11 are not in event A or B.
There are 12 possible outcomes, the numbers 1 to 12.
There are a total of 6 outcomes that satisfy event A or event B ( 12 is only counted once even though it satisfies event A and event B ).
So P(A \cup B)=\frac{6}{12}.
Intersection
P(A \cap B) or ‘A intersection B’ is the chance of picking any outcome that is satisfied by event A and event B, the joint probability of the events.
In a Venn diagram it would be presented like this.
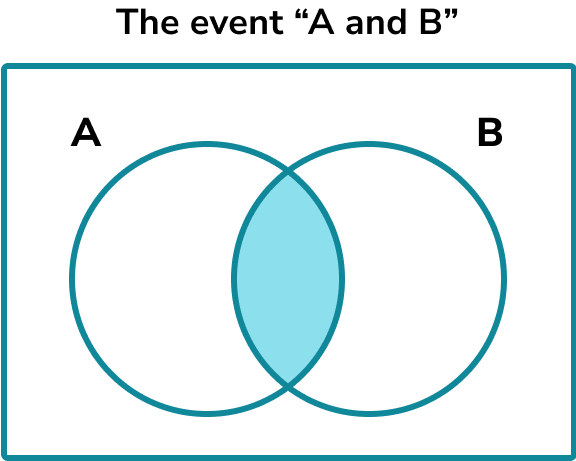
For example, \xi is the set of numbers, 1-12. \ A and B are subsets of \xi .
A = multiples of 3.
B = multiples of 4.
One of the numbers is picked at random. Find the probability P(A \cap B).
Event A are the multiples of 3 = 3, 6, 9, 12 .
Event B are the multiples of 4 = 4, 8, 12 .
The numbers 1, 2, 5, 7, 10 and 11 are not in event A or B.
There are 12 possible outcomes, the numbers 1 to 12.
There is only 1 number that satisfies event A and event B, the number 12.
So P(A \cap B)=\frac{1}{12}.
How to use probability notation
In order to use probability notation to calculate the probability of an event:
- Identify the event.
- Identify how many possible outcomes there are.
- Identify how many times the event occurs.
- Write this as a probability.
Explain how to use probability notation

Probability notation worksheet
Get your free probability notation worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONProbability notation worksheet
Get your free probability notation worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONRelated lessons on describing probability
Probability notation is part of our series of lessons to support revision on describing probability. You may find it helpful to start with the main describing probability lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Probability notation examples
Example 1: probability of an event

Event A is picking a circle.
Event B is picking a square.
Event C is picking a triangle.
Event D is picking a star.
What is P(C)?
- Identify the event.
Event C is the probability of picking a triangle.
2Identify how many possible outcomes there are.
There are 10 possible outcomes as there are 10 shapes in the bag.
3Identify how many times the event occurs.
There are two triangles so the expected value is 2.
4Write this as a probability.
\frac{2}{10}
Example 2: probability of an event not happening

Event A is picking a circle.
Event B is picking a square.
Event C is picking a triangle.
Event D is picking a star.
What is P(D’)?
Identify the event.
Event D is the probability of picking a star. In this example we want the complement of D so we want any shape that is not a star.
Identify how many possible outcomes there are.
There are 10 possible outcomes as there are 10 shapes in the bag.
Identify how many times the event occurs.
There are 9 shapes that are not a star.
Write this as a probability.
Example 3: probability of event A or event B or both

Event A is picking a blue shape.
Event B is picking a triangle.
Calculate P(A \cup B).
Identify the outcomes that are event \bf{A} or event \bf{B} .
A blue shape or a triangle needs to be picked.
Identify how many possible outcomes there are.
There are 10 shapes in the bag.
Identify how many times the event occurs.
Event A: \ 3 shapes
Event B: \ 2 triangles
There are a total of 5 possible outcomes.
Write this as a probability.
P(A \cup B) = \frac{5}{10} \ or \ 0.5.
Example 4: probability of event A or event B or both
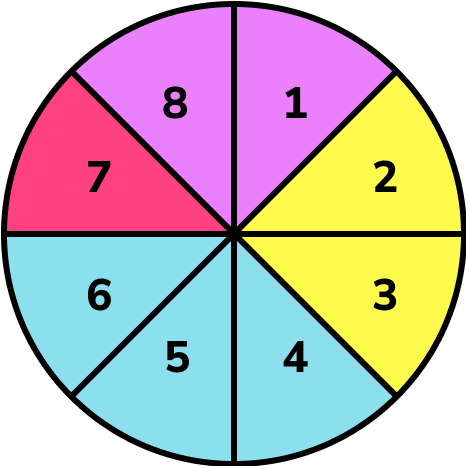
Event A the spinner landing on blue.
Event B is the spinner landing on an even number.
Calculate P(A \cup B).
Identify the outcomes that are event \bf{A, B} or both.
The spinner needs to land on a blue section or a section numbered 2, 4, 6 or 8.
Identify how many possible outcomes there are.
There are 8 sections on the spinner.
Identify how many times the event occurs.
Event A: \ 3 sections
Event B: \ 2, 4, 6, 8
There are a total of 5 possible outcomes ( 4 and 6 satisfy event A and event B ).
Write this as a probability.
Example 5: probability of event A and event B
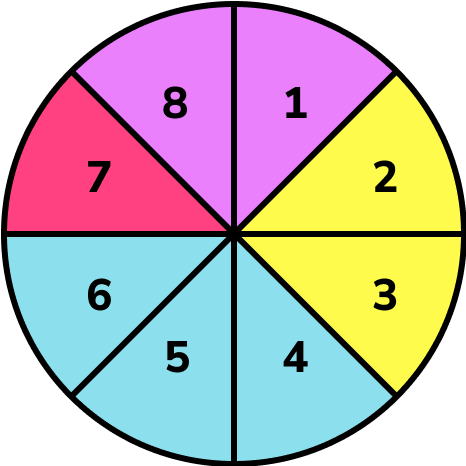
Event A is the spinner landing on blue.
Event B is the spinner landing on an even number.
Calculate P(A \cap B).
Identify the outcomes that are event \bf{A} and event \bf{B} .
The spinner needs to land on a blue section and an even number.
Identify how many possible outcomes there are.
There are 8 sections on the spinner.
Identify how many times the event occurs.
Two sections are blue and an even number.
There are 2 possible outcomes.
Write this as a probability.
Example 6: probability of event A and event B
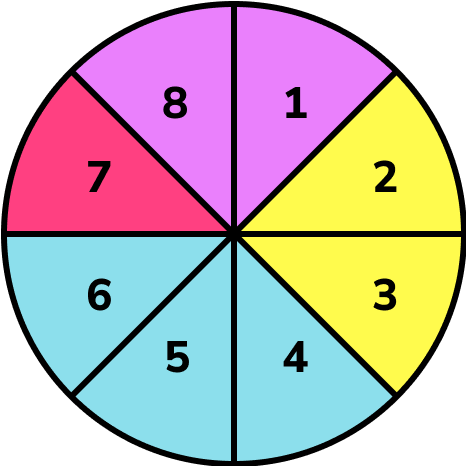
Event A is the spinner landing on red.
Event B is the spinner landing on an even number.
Calculate P(A \cap B).
Identify the outcomes that are event \bf{A} and event \bf{B} .
The spinner needs to land on a red section and an even number.
Identify how many possible outcomes there are.
There are 8 sections on the spinner.
Identify how many times the event occurs.
The only red section is an odd number.
There are 0 possible outcomes.
Write this as a probability.
Common misconceptions
- Confusing ‘union’ and ‘intersection’
P(A \cup B) and P(A \cap B) are similar and can easily be interchanged due to confusion.
- Assuming all expected values are \bf{A \cup B}
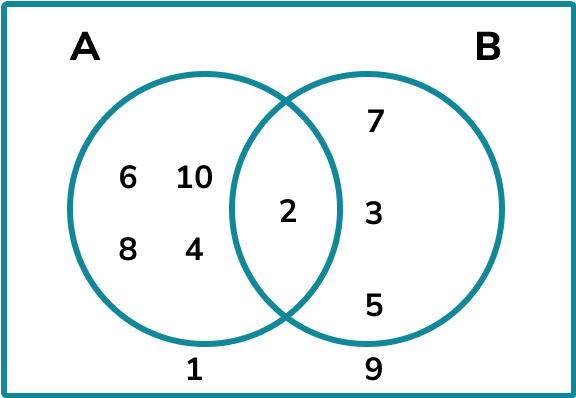
Some values may be in the universal set but not be satisfied by event A or event B, it might sit outside.
For example, this Venn diagram displays two numbers, 1 and 9, that are not satisfied by event A or event B but are in the universal set. The universal set is notated with the greek letter \xi.
- Incorrect use of and/or rule for independent events and conditional probability
When calculating the probability of event A or event B, you need to add the probabilities.
When calculating the probability of event A and event B, you need to multiply the probabilities.
- Misinterpreting the notation
Set notation includes use of capital letters, lower case letters and greek letters. These are specific and cannot be interchanged.
For example, set ‘A’ could be the even numbers and set ‘a’ could be odd numbers.
- Listing outcomes
When there are two or more events we need to use systematic listing strategies to include all the permutations.
Practice probability notation questions
1.

Event A is picking a blue marble.
Event B is picking a green marble.
Event C is picking a red marble.
Work out P(B).




The notation P(B) means we want the probability of event B. Event B is picking a green marble.
There are 5 green marbles and 8 marbles in total.
So, P(B) = \frac{5}{8}.
2.

Event A is picking a blue marble.
Event B is picking a green marble.
Event C is picking a red marble.
Work out P(C').




The notation P(C') means we want the probability that it is not event C. Event C is picking a red marble.
There are two red marbles and six marbles that are not red.
There are 8 marbles in total.
So, P(C') = \frac{6}{8}.
3. A fair six sided dice is rolled.
Event A is the dice landing on an even number.
Event B is the dice landing on ‘1’.
Calculate P(A \cup B).




The notation P(A \cup B) means in A, or B, or both. There are three even numbers and one ‘1’.
Therefore there are 4 possible outcomes that satisfy event A, event B, or both.
There are 6 outcomes in total.
So, P(A \cup B) = \frac{4}{6}.
4. A fair six sided dice is rolled.
Event A is the dice landing on an even number.
Event B is the dice landing on a prime number.
Calculate P(A \cup B).




The notation P(A \cup B) means in A, or B, or both. There are three even numbers (2, 4, 6) and three prime numbers (2, 3, 5).
‘2’ satisfies both event A and event B so there are 5 possible outcomes that satisfy event A and event B.
There are 6 outcomes in total.
So, P(A \cup B) = \frac{5}{6}.
5. A fair six sided dice is rolled.
Event A is the dice landing on an even number.
Event B is the dice landing on ‘2’.
Calculate P(A \cap B).




The notation P(A \cap B) means in A and B. There are three even numbers and one ‘2’.
Therefore there is 1 possible outcome that satisfies event A and event B.
There are 6 outcomes in total.
So, P(A \cap B) = \frac{1}{6}.
6. A fair six sided dice is rolled.
Event A is the dice landing on an odd number.
Event B is the dice landing on a prime number.
Calculate P(A \cap B).




The notation P(A \cap B) means in A and B. There are three odd numbers (1, 3, 5) and three prime numbers (2, 3, 5).
‘3 and 5' satisfies both event A and event B so there are 2 possible outcomes.
There are 6 outcomes in total.
So, P(A \cap B) = \frac{2}{6}.
Probability notation GCSE questions
1. \xi = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15\}
A = square numbers
B = odd numbers
(a) Calculate P(B).
b) Calculate P(A \cup B).
(2 marks)
(a)
P(B) = \frac{8}{15}
(1)
(b)
P(A \cup B) = \frac{9}{15}, or equivalent. For example, \frac{3}{5} or 0.6.
(1)
2. (a) Here is a Venn diagram.

(a) Calculate P(A').
b) Calculate P(A \cap B).
(2 marks)
(a)
P(A') = 0.5 or equivalent. For example, \frac{5}{10} or \frac{1}{2}.
(1)
(b)
P(A \cap B) = 0.1 or equivalent. For example, \frac{1}{10}.
(1)
3. \xi = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}
A = \{multiples of 4\}
\begin{aligned} &A \cap B = \{4, 12\} \\ &A \cup B = \{1, 2, 3, 4, 6, 8, 9, 12\} \end{aligned}
(a) Calculate P(B).
(b) Calculate P(A').
(2 marks)
(a)
P(B) = \frac{6}{12}, or equivalent. For example, \frac{1}{2} or 0.5.
(1)
(b)
P(A') = \frac{9}{12}, or equivalent. For example, \frac{3}{4} or 0.75.
(1)
Learning checklist
You have now learned how to:
-
Interpret probability notation to calculate the probability of an event
-
Apply probability notation to sets and Venn diagrams
-
Interpret notation which includes capital letters, lower case letters and greek letters
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.