GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Arithmetic Equivalent fractions Highest common factor BIDMASThis topic is relevant for:

Simplifying Fractions
Here we will learn about simplifying fractions, including how to write fractions in their simplest form using common factors.
There are also simplifying fractions worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is simplifying fractions?
Simplifying fractions is reducing fractions to their simplest form.
To do this we look at the numerator (the top number) and the denominator (the bottom number) and find a common factor that we can use to cancel the fraction down to its lowest terms. The numerator and denominator are always whole numbers.
For example, the fraction \frac{5}{10} can be simplified to \frac{1}{2} as both the numerator and denominator have 5 as a factor.
\frac{5}{10}=\frac{1\times 5}{2\times 5}=\frac{1}{2}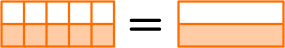
The common factor of 5 cancels on the top and the bottom, leaving us with the simplified version.
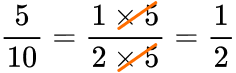
What is simplifying fractions?

How to simplify fractions
In order to simplify fractions:
- Look at the numerator and the denominator and find the highest common factor.
- Divide both the numerator and the denominator by the HCF.
- Write the fraction in its simplest terms.
Explain how to simplify fractions

Simplifying fractions worksheet

Get your free simplifying fractions worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Simplifying fractions worksheet

Get your free simplifying fractions worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on fractions
Simplifying fractions is part of our series of lessons to support revision on fractions. You may find it helpful to start with the main fractions lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Simplifying fractions examples
Example 1: simple fractions with a prime HCF
Write the following fraction in its simplest form \frac{10}{14}.
- Look at the numerator and the denominator and find the highest common factor.
The numerator of the fraction is 10.
The denominator of the fraction is 14.
The highest common factor of 10 and 14 is 2.
2Divide both the numerator and the denominator by the HCF.
10 \div 2=5 14 \div 2=7The new numerator is 5 and the new denominator is 7.
5 and 7 have no common factors other than 1.
So the fraction will be in its simplest form.
3Write the fraction in its simplest terms.
\frac{10}{14}=\frac{5}{7}Example 2: simple fractions with a prime HCF
Write the following fraction in its simplest form \frac{15}{40}.
Look at the numerator and the denominator and find the highest common factor.
The numerator of the fraction is 15.
The denominator of the fraction is 40.
The highest common factor of 15 and 40 is 5.
Divide both the numerator and the denominator by the HCF.
40 \div 5=8
The new numerator is 3 and the new denominator is 8.
3 and 8 have no common factors other than 1.
So the fraction will be in its simplest form.
Write the fraction in its simplest terms.
Example 3: simple fractions with a non-prime HCF
Write the following fraction in its simplest form \frac{52}{100}.
Look at the numerator and the denominator and find the highest common factor.
The numerator of the fraction is 52.
The denominator of the fraction is 100.
The highest common factor of 52 and 100 is 4.
Divide both the numerator and the denominator by the HCF.
100 \div 4=25
The new numerator is 13 and the new denominator is 25.
13 and 25 have no common factors other than 1.
So the fraction will be in its simplest form.
Write the fraction in its simplest terms.
Example 4: simple fractions with a non-prime HCF
Write the following fraction in its simplest form \frac{160}{400}.
Look at the numerator and the denominator and find the highest common factor.
The numerator of the fraction is 160.
The denominator of the fraction is 400.
The highest common factor of 160 and 400 is 80.
Divide both the numerator and the denominator by the HCF.
400 \div 80=5
The new numerator is 2 and the new denominator is 5.
2 and 5 have no common factors other than 1.
So the fraction will be in its simplest form.
Write the fraction in its simplest terms.
Example 5: algebraic fractions
Write the following fraction in its simplest form \frac{4a^3b}{24ab^2}.
Look at the numerator and the denominator and find the highest common factor.
We need to look at each component of the fractions in turn. The number part and the variables part.
\frac{4a^3b}{24ab^2}=\frac{4\times a^3\times b}{24\times a\times b^2}
The number part is \frac{4}{24}.
The highest common factor of 4 and 24 is 4.
The variable part of the numerator is a^{3}b and the variable part of the denominator is ab^{2}. The highest common factor of these parts is ab.
You could also simplify them as a fraction on their own, \frac{a^{3}b}{ab^{2}}, using the laws of indices.
So the highest common factor of 4a^{3}b and 24ab^2 is 4ab.
Divide both the numerator and the denominator by the HCF.
The new numerator is a^2 and the new denominator is 6b.
a^2 and 6b have no common factors other than 1.
So the fraction will be in its simplest form.
Write the fraction in its simplest terms.
Example 6: algebraic fractions
Write the following fraction in its simplest form \frac{x^2+4x}{x^2-16}.
Look at the numerator and the denominator and find the highest common factor.
We need to factorise the numerator and factorise the denominator.
x^2+4x=x(x+4)
And the denominator factorises to x^2-16=(x+4)(x-4).
The highest common factor of x^{2}+4x and x^{2}-16 is (x+4).
Divide both the numerator and the denominator by the HCF.
(x+4)(x-4) \div (x+4)=x-4
The new numerator is x and the new denominator is (x-4).
x and (x-4) have no common factors other than 1.
So the fraction will be in its simplest form.
Write the fraction in its simplest terms.
There is no need for the brackets on the denominator.
Common misconceptions
- Simplified fractions must use integers
The numerator and denominator of a fraction must both be integers (whole numbers). The final answer can not have decimals.
- Write a fraction in its simplest form or simplify fully
You can simplify a fraction by using any of the common factors of the numerator and the denominator of a fraction. But you may need to cancel more than once to make sure you have written the fraction in its simplest form. Using the highest common factor means that you will only have to cancel once.
For example, write the following fraction in its simplest form.
\frac{20}{60}
20 and 60 have a common factor of 10.
We can cancel the common factor of 10.
\frac{20}{60}=\frac{2\times10}{6\times10}=\frac{2}{6}
But the first fraction has not been written in its simplest form as the new numerator 2 and the new denominator 6 also share a common factor of 2.
\frac{2}{6}=\frac{1\times2}{3\times2}=\frac{1}{3}
The fraction in its simplest form is \frac{1}{3}.
- Simplified fractions can only be made by using common factors
You cannot simplify fractions by using addition.
For example,
This is an incorrect method of cancelling.
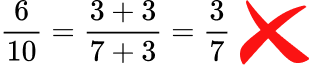
This is a correct method of cancelling.
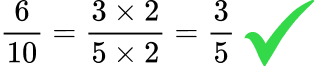
This is especially relevant when simplifying algebraic fractions.
For example,
This is an incorrect method of cancelling.
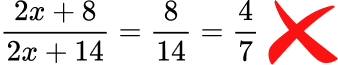
This is a correct method of cancelling.
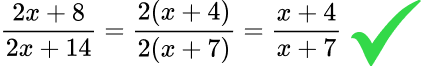
Practice simplifying fractions questions
1. Simplify \frac{3}{12}.




The highest common factor of the numerator and the denominator is 3.
3 \div 3=1
12 \div 3=4
2. Simplify \frac{15}{35}.




The highest common factor of the numerator and the denominator is 5.
15 \div 5=3
35 \div 5=7
3. Simplify fully \frac{30}{120}.




The highest common factor of the numerator and the denominator is 30.
30 \div 30=1
120 \div 30=4
4. Simplify fully \frac{45}{135}.




The highest common factor of the numerator and the denominator is 45.
45 \div 45 =1
135 \div 45=3
5. Simplify fully \frac{10c^3d^2}{45cd^4}.




The highest common factor of the numerator and denominator is 5cd^{2}.
10c^{3}d^{2} \div 5cd^{2}= 2c^2
45cd^{4} \div 5cd^{2}= 9d^2
6. Simplify \frac{x^2+2x}{x^2-3x}.




Factorise the numerator and the denominator.
\frac{x^2+2x}{x^2-3x}=\frac{x(x+2)}{x(x-3)}
We can then see that the common factor is x. We can cancel by the x.
\frac{x^2+2x}{x^2-3x}=\frac{x(x+2)}{x(x-3)}=\frac{x+2}{x-3}
Simplifying fractions GCSE questions
1. Simplify these fractions.
Give your answer as a fraction in its simplest form.
(a) \frac{7}{21}
(b) \frac{6}{108}
(3 marks)
(a) \frac{1}{3}
(1)
(b)
Writing the fraction as a simplified fraction, but not fully simplified.
For example, \frac{3}{54} or \frac{2}{36}.
(1)
\frac{1}{18}(1)
2. Belle says that \frac{30}{60} is \frac{3}{6} when fully simplified.
Lucy says that \frac{30}{60} is \frac{1}{2} when fully simplified.
Who is correct? Explain your answer.
(2 marks)
Lucy
(1)
For a correct explanation using HCF.
For example, Belle has only simplified by using a common factor of 10.
Lucy has simplified fully by using the highest common factor of 30.
(1)
3. Write these decimals as fractions.
Give your answer as a fraction in its simplest form.
(a) 0.3
(b) 0.55
(3 marks)
(a) \frac{3}{10}
(1)
(b)
Writing the decimal as a fraction.
For example, \frac{55}{100}.
(1)
\frac{11}{20}(1)
4. Write these percentages as fractions.
Give your answer as a fraction in its simplest form.
(a) 40\%
(b) 62.5\%
(4 marks)
(a)
Writing the percentage as a fraction.
For example, \frac{40}{100}.
(1)
\frac{2}{5}(1)
(b)
Writing the percentage as a fraction.
For example, \frac{62.5}{100} or \frac{625}{1000}.
(1)
\frac{11}{20}(1)
5. Simplify these algebraic fractions.
Give your answer as a fraction in its simplest form.
(a) \frac{3a^{2}b}{12ab^{3}}
(b) \frac{x^{2}-25}{x^{2}-5x}
(4 marks)
(a)
For 2 out of 3 correct components,
\frac{1}{4}, \ a, \ \frac{1}{b^{2}}.(1)
\frac{a}{4b^{2}}(1)
(b)
For factorising the numerator or the denominator,
(x+5)(x-5) or x(x-5).
(1)
\frac{x+5}{x}(1)
Learning checklist
You have now learned how to:
-
Simplify fractions
-
Simplify algebraic fractions by factorising
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.