6. Solve the simultaneous equations: \begin{aligned} y&=x+3\\ y&=x^2+5x-2\\ \end{aligned}

$ x= -5 , y= -2 $ or $ x= 1 , y=4 $

$ x= -5 , y= 4 $ or $ x= 1 , y= -2 $

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Straight line graphs Plotting quadratic graphs

This topic is relevant for:

GCSE Maths Algebra Simult. Equations

Solving Simult. Equations Graphically

Solving Simultaneous Equations Graphically

Here we will learn how to solve simultaneous equations graphically including linear and quadratic simultaneous equations.

There are also solving simultaneous equations graphically worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is solving simultaneous equations graphically?

Solving simultaneous equations graphically is the process that allows us to solve two or more algebraic equations that share variables by sketching their graphs.

The point (or points) of intersection give(s) the solution(s) to the simultaneous equations.

This is because at the point of intersection the two equations are equal to one another and therefore the values of the variables are the same for both equations.

What is solving simultaneous equations graphically?

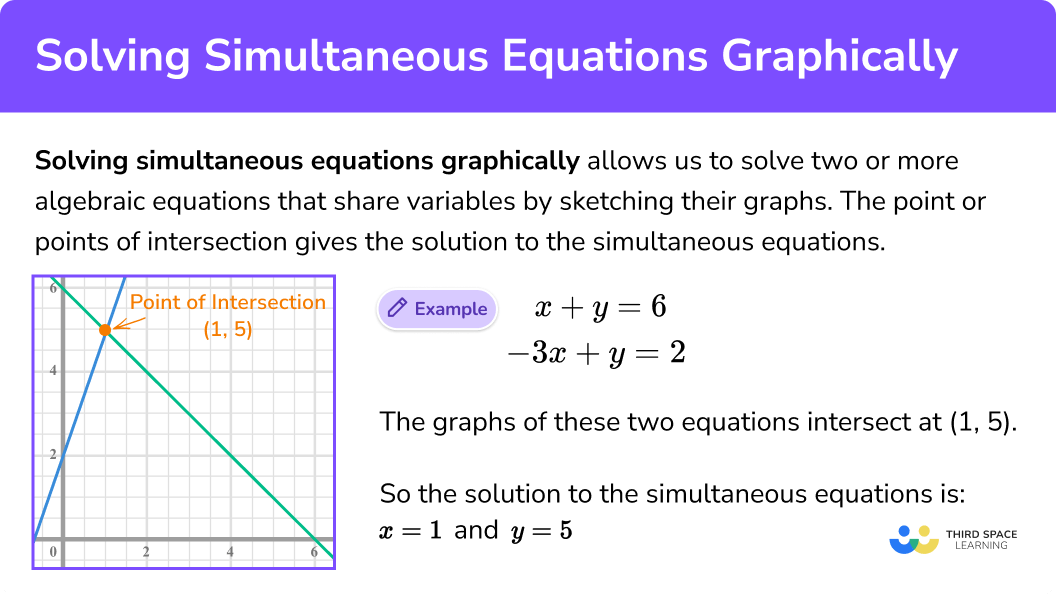
Solving linear simultaneous equations graphically

E.g. Solve the pair of simultaneous equations

\[\begin{aligned} x +y &= 6\\ -3x +y &=2\\ \end{aligned}\]

Solving Simultaneous Equation Graphically image 1

When we draw the graphs of these two equations,
we can see that they intersect at (1, 5).

So the solution to the simultaneous equations is:

x = 1 and y = 5

We can prove this is the solution by substituting the values into the original equations:

x = 1, y = 5

\[\begin{aligned} x+y&=6\\ 1+5&=6\\ \end{aligned}\]

\[\begin{aligned} -3x+y&=2\\ -3(1)+5=2\\ -2+5=2\\ \end{aligned}\]

Solving quadratic simultaneous equations graphically

One key difference with simultaneous equations containing a quadratic element is we can expect multiple answers. This is because of the way linear and non-linear functions can intersect.

Here a linear function is intersecting a quadratic function which has a shape known as a parabola.

Notice that the two points of intersection means that the simultaneous equations have two valid solutions.

Solving Simultaneous Equation Graphically image 2

E.g.

\[\begin{aligned} x+y&=4 \\ y&=x^{2}+4x-2 \\ \end{aligned}\]

Solving Simultaneous Equation Graphically image 3

When graphed these two equations intersect at two points (−6, 10) and (1, 3)
So therefore the simultaneous equations has two valid solutions

So the solutions to the simultaneous equations are:

\[x = -6, y = 10\]

And

\[x =1, y = 3\]

We can prove these are the solutions to the simultaneous equations by substituting the values into the original equations:

\[x = -6, y = 10\]

\[\begin{aligned} x+y=4 \\ -6+10=4 \end{aligned}\]

\[\begin{aligned} y&=x^{2}+4x-2 \\ 10&=(-6)^2+4(-6)-2\\ 10&=36-24-2\\ \end{aligned}\]

And

\[x =1, y = 3\]

\[\begin{aligned} x+y=4 \\ 1+3=4\\ \end{aligned}\]

\[\begin{aligned} y&=x^{2}+4x-2 \\ 3&=(1)^2+4(1)-2\\ 3&=1+4-2\\ \end{aligned}\]

Solving simultaneous equations graphically is part of our series of lessons to support revision on simultaneous equations. You may find it helpful to start with the main simultaneous equations lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

How to solve simultaneous equations graphically

In order to solve simultaneous equations graphically:

Identify if the equations are linear or quadratic (or other non-linear)
Draw each equation on the same set of axes
Find the coordinates where the lines intersect
State the values of the variable where the lines intersect and clearly state your answer (if you have multiples values of a variable ensure you match the correct pair)

How to solve simultaneous equations graphically

Solving simultaneous equations graphically worksheet

Get your free solving simultaneous equations graphically worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Solving simultaneous equations graphically worksheet

Get your free solving simultaneous equations graphically worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Solving simultaneous equations graphically examples

Example 1: solving linear simultaneous equations where ‘y’ is the subject of the formula

Solve this pair of simultaneous equations graphically:

\[\begin{aligned} y&=2x+1\\ y&=4x+3 \end{aligned}\]

Identify if the equations are linear or quadratic

Both the equations are linear.
This means you will be drawing two straight lines which will intersect at one point only.

2Draw each equation on the same set of axes

Solving Simultaneous Equation Graphically example 1

3Find the coordinates where the lines intersect

Solving Simultaneous Equation Graphically example 1.2

The lines intersect (cross) at the coordinate (−1, −1)

4State the values of the variable where the lines intersect and clearly state your answer (if you have multiples values of a variable ensure you match the correct pair)

\[\begin{aligned} x&=-1\\ y&=-1 \end{aligned}\]

Example 2: solving linear simultaneous equations where ‘y’ is not the subject of the formula

Solve this pair of simultaneous equations graphically:

\[\begin{aligned} 2x+4y&=14\\ 4x-4y&=4 \end{aligned}\]

Identify if the equations are linear or quadratic

Both the equations are linear. This means you will be drawing two straight lines which will intersect at one point only.

Draw each equation on the same set of axes

Solving Simultaneous Equation Graphically example 2.1

Find the coordinates where the lines intersect

Solving Simultaneous Equation Graphically example 2.2

The lines intersect (cross) at the coordinate (3, 2)

State the values of the variable where the lines intersect and clearly state your answer (if you have multiples values of a variable ensure you match the correct pair)

\[\begin{aligned} x&=3\\ y&=2 \end{aligned}\]

Example 3: solving linear simultaneous equations where ‘y’ is not the subject of the formula

Solve this pair of simultaneous equations graphically:

\[\begin{aligned} 3x+2y&=8\\ 2x+5y&=-2 \end{aligned}\]

Identify if the equations are linear or quadratic

Both the equations are linear.
This means you will be drawing two straight lines which will intersect at one point only.

Draw each equation on the same set of axes

Solving Simultaneous Equation Graphically example 3.1

Find the coordinates where the lines intersect

Solving Simultaneous Equation Graphically example 3.2

The lines intersect (cross) at the coordinate (-4, −2)

State the values of the variable where the lines intersect and clearly state your answer (if you have multiples values of a variable ensure you match the correct pair)

\[\begin{aligned} x&=-4\\ y&=-2 \end{aligned}\]

Example 4: solving simultaneous equations (one linear and one quadratic) where ‘y’ is the subject of the formula

Solve this pair of simultaneous equations graphically:

\[\begin{aligned} y&=x+3\\ y&=x^2+5x-2 \end{aligned}\]

Identify if the equations are linear or quadratic

The first equation here is linear.
This will therefore be drawn as a straight line on a set of axes.

The second equation is quadratic.
This will therefore be drawn as a parabola on a set of axes.

If you consider the straight line and parabola there are three possible ways in which they can intersect.

Solving Simultaneous Equation Graphically example 4.1

Note:

At GCSE most answers have two points of intersection.

A function with a quadratic element in more than one variable can create other curved graphs, E.g. x²+y²=4 will produce a circle.

Draw each equation on the same set of axes

Solving Simultaneous Equation Graphically example 4.2

Find the coordinates where the lines intersect

You will notice that the two functions intersect at two points.

Solving Simultaneous Equation Graphically example 4.3

The lines intersect (cross) at the coordinates (−5, −2) and (1, 4).

State the values of the variable where the lines intersect and clearly state your answer (if you have multiples values of a variable ensure you match the correct pair)

\[x= -5, y= -2 \]

\[x= 1, y= 4 \]

Notice the use of the word or. This is because either answer is a valid solution to the simultaneous equations.

Example 5: solving simultaneous equations (one linear and one circle)

Solve this pair of simultaneous equations graphically:

\[\begin{aligned} y^2+x^2&=29\\ x+7&=y\\ \end{aligned}\]

Identify if the equations are linear or quadratic

The first equation here is linear.
This will therefore be drawn as a straight line on a set of axes.

The second equation has quadratic elements in both variables.

It contains the square of both the x and y variables.
This will therefore produce a circle.

Draw each equation on the same set of axes

Solving Simultaneous Equation Graphically example 5.1

Find the coordinates the lines intersect

Solving Simultaneous Equation Graphically example 5.2

You will notice that the two functions intersect at two points.

The lines intersect (cross) at the coordinates (−5, 2) and (−2, −5).

State the values of the variable where the lines intersect and clearly state your answer (if you have multiples values of a variable ensure you match the correct pair)

\[x= -5, y=2 \]

\[x= -2, y= 5\]

Common misconceptions

Incorrect drawing of graphs

A common mistake is to incorrectly the draw the graphs. It can be helpful to:

Complete a table of values for the equation
Make y the subject of the formula (especially for linear functions)
Consider the gradient of the graph (for linear functions)
Consider where the graph intersects the x and y axes

Multiple points of intersection

Remember linear and non-linear functions can intersect at 0, 1 or 2 points. If the lines have multiple points of intersection make sure to match the correct value of x and y.

Practice solving simultaneous equations graphically questions

Yes

Sometimes

Need more information

Solving Simultaneous Equation Graphically practice Q1

Two linear functions cannot intersect at two points. If they cross each other it will be at one point only.

Always

Never

Sometimes

Need more information

Solving simultaneous equations graphically practice Q4

A parabola and a line can intersect at $2$ points but they can also intersect at $1$ point or $0$ points

Parallel

Perpendicular

Far away from each other

Incorrectly drawn

Practice q3

Two lines that never meet (never intersect) are parallel to one another.

x= -2.5 , y=-11

x= 2.5, y= -11

x=2.5 , y=11

x=11 , y=2.5

Practice Q4 simultaneous equations solved graphically

x= 4 , y=- 9

x= -4 , y=9

x= 4 , y= 9

x= -4 , y= -9

Solving Simultaneous Equations Graphically Practice Q5 explanation

x= -5 , y= -1

x= -5 , y= -2

x= 1 , y=4

x= 1 , y=4

x= -5 , y= 4

x= 1 , y= -2

Solving Simultaneous Equations Graphically practice Q6

Solving simultaneous equations graphically GCSE questions

1. The graphs of the straight lines with equations

\begin{aligned} 3y+2x&=12\\ y&=x+4\\ \end{aligned}

have been drawn on the grid below:

Solving Simultaneous Equations Graphically GCSE Q1

Use the graphs to solve the simultaneous equations

\begin{aligned} 3y+2x&=12\\ y&=x+4\\ \end{aligned}

(2 marks)

Show answer

x=0

(1)

y=4

(1)

2. The graphs of the straight lines with equations

\begin{aligned} 4y-2x&=8\\ y&=x\\ \end{aligned}

have been drawn on the grid below:

Solving Simultaneous Equations Graphically

Use the graphs to solve the simultaneous equations

\begin{aligned} 4y-2x&=8\\ y&=x\\ \end{aligned}

(2 marks)

Show answer

x=4

(1)

y=4

(1)

3. The graphs of the straight lines with equations

\begin{aligned} y&=\frac{x}{2}+2\\ 2y+3x&=12\\ \end{aligned}

have been drawn on the grid below:

Use the graphs to solve the simultaneous equations

\begin{aligned} y&=\frac{x}{2}+2\\ 2y+3x&=12\\ \end{aligned}

(2 marks)

Show answer

x=2

(1)

y=3

(1)

4. By drawing the graphs of

\begin{aligned} y&=3x+5x\\ x-2y+6&=0\\ \end{aligned}

Solve the simultaneous equations:

\begin{aligned} y&=3x+5x\\ x-2y+6&=0\\ \end{aligned}

(3 marks)

Show answer

Both graphs drawn correctly with intersection

(1)

x=0.4

(1)

y=3.2

(1)

5. By drawing the graphs of

\begin{aligned} x+y&=4\\ y&=x^2+3x-1 \end{aligned}

Solve the simultaneous equations:

\begin{aligned} x+y&=4\\ y&=x^2+3x-1 \end{aligned}

(3 marks)

Show answer

Both graphs drawn correctly with intersection

(1)

$x= -5$ and $y=9$

(1)

$x= 1$ and $y=3$

(1)

Learning checklist

You have now learned how to:

Work with coordinates in all four quadrants

Identify and interpret the intercepts of linear functions graphically

Identify and interpret the intercepts of quadratic functions graphically

Interpret graphs of linear functions and quadratic functions

Solve two simultaneous equations with two variables; linear/linear

Solve two simultaneous equations with two variables; linear/quadratic

The next lessons are

Maths formulas
Types of graphs
Interpreting graphs

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.