GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Factorising quadratics Expanding brackets Simplifying algebraic expressionsThis topic is relevant for:

Solving Equations
Here we break down everything you need to know about solving equations. You’ll learn what linear and quadratic algebraic equations are, and how to solve all the different types of them.
At the end you’ll find solving equations worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is an equation?
An equation is a mathematical expression that contains an equals sign.
E.g.
There are two sides to an equation, with the left side being equal to the right side.
Equations will often involve algebra and contain unknowns (variables) which we often represent with letters such as
We can solve simple equations and more complicated equations to work out the value of these unknowns; they could involve fractions, decimals or integers.
Step-by-step guide: Forming and solving equations
What is an equation?


Solving equations worksheets

Get your free solving equations worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Solving equations worksheets

Get your free solving equations worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEHow to solve equations
In order to solve equations, we need to work out the value of the unknown variable by adding, subtracting, multiplying or dividing both sides of the equation by the same value.
To solve equations step by step
- Multiply out any brackets using the distributive property
- Multiply or divide the same number to both sides of the equation
- Add or subtract the same number to both sides of the equation
In GCSE Maths there are two main types of equations that we need to solve: linear equations and quadratic equations. Methods of solving each are provided below.
Explain how to solve equations

Solving equations methods
Within solving equations, you will find lessons on linear equations and quadratic equations.
Each method of solving equations is summarised below. For detailed examples, practice questions and worksheets on each one follow the links to the step by step guides.
1. Linear equations
There are 5 main types of linear equations we can solve.
Example of solving an equation with:
- One unknown
2Unknown on both sides
3With brackets
4With fractions
Step-by-step guide: Equations with fractions
5Powers (exponents) and roots
We can check that our solution is correct by substituting it into the original equation.
Step-by-step guide: Linear equations
Step-by-step guide: Iteration maths
2. Quadratic equations
There are 4 main ways to solve quadratic equations.
Example of solving a quadratic equation by:
- Factorising
Step-by-step guide: Solving quadratic equations by factorising
2Quadratic Formula
Step-by-step guide: Quadratic formula
3Complete the square
Step-by-step guide: Completing the square
4Graphically
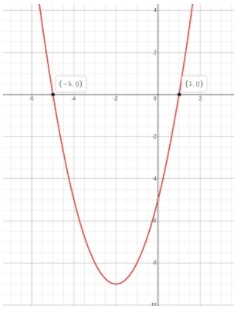
The solutions/roots are found when the graph equals 0 (crosses the x-axis).
We can check that our solution is correct by substituting it into the original equation.
Step-by-step guide: Solving quadratic equations graphically
See also: Quadratic equations
Practice solving equations questions
1. Solve: 4x-2=14




Add 2 to both sides
4x=16
Divide both sides by 4
x=4
2. Solve: 3x-8=x+6




Add 8 to both sides
3x=x+14
Subtract x from both sides
2x=14
Divide both sides by 2
x=7
3. Solve: 3(x+3)=2(x-2)




Expanding the brackets
3x+9=2x-4
Subtract 9 from both sides
3x=2x-13
Subtract 2x from both sides
x=-13
4. Solve: \frac{2 x+2}{3}=\frac{x-3}{2}




Multiply by 6 (the lowest common denominator) and simplify
2(2x+2)=3(x-3)
Expand the brackets
4x+4=3x-9
Subtract 4 from both sides
4x=3x-13
Subtract 3x from both sides
x=-13
5. Solve: \frac{3 x^{2}}{2}=24

x=\pm 2



Multiply both sides by 2
3 x^{2}=48
Divide both sides by 3
x^{2}=16
Square root both sides
x=\pm 4
6. Solve by factorising: x^{2}-13 x+30=0




Factorise as a double bracket
(x-3)(x-10)=0
Set each bracket equal to zero and solve, hence
x=3 or x=10
7. Solve by factorising: 2 x^{2}+3 x-20=0




Factorise as a double bracket
(2x-5)(x+4)
Set each bracket equal to zero and solve, hence
x=\frac{5}{2}, \; x=-4
8. (H) Solve by using the quadratic formula: x^{2}-4 x-3=0
give your answer to 3 significant figures




Substitution into the quadratic formula gives
x=\frac{-(-4)+\sqrt{(-4)^{2}-4(1)(-3)}}{2(1)} \quad \quad \quad \; x=\frac{-(-4)-\sqrt{(-4)^{2}-4(1)(-3)}}{2(1)} \\
x=2+\sqrt{7} \quad \quad \quad \quad \quad \quad \quad \quad x=2-\sqrt{7} \\
x=4.65 \; (3.5 . f) \quad \quad \quad\quad \quad \quad x=-0.646 \; (3.s.f)
9. (H) Solve by using the quadratic formula: 2 x^{2}+4 x-4=0
give your answer to 3 significant figures




Substitution into the quadratic formula gives
x=\frac{-(4)+\sqrt{(4)^{2}-4(2)(-4)}}{2(2)} \quad \quad \quad \; x=\frac{-(4)+\sqrt{(4)^{2}-4(2)(-4)}}{2(2)} \\
x=-1+\sqrt{3} \quad \quad \quad \quad \quad \quad \quad \quad x=-1-\sqrt{3} \\
x=0.732 \; (3.s.f) \quad \quad \quad \quad \quad \quad x=-2.73 \; (3.s.f)
10. (H) Solve by completing the square: x^{2}-6 x+5=0




Completing the square
(x-3)^{2}-4=0
Add 4 to both sides
(x-3)^{2}=4
Square root both sides
x-3=\pm 2
Add 3 to both sides
x=3\pm 2
So x=5, \; x=1
Solving equations GCSE questions
Learning checklist
-
Use algebraic methods to solve linear equations
-
Solve quadratic equations algebraically by factorising
-
Solve quadratic equations algebraically by completing the square (H)
-
Solve quadratic equations algebraically by using the quadratic formula (H)
-
Solve quadratic equations by finding approximate solutions using a graph
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.