One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Substitution Plotting graphs Simultaneous equations Laws of indices Geometric sequences Compound interestThis topic is relevant for:

Exponential Function
Here we will learn about the exponential function, graphs of exponential functions, finding exponential equations and its links to compound interest and geometric sequences.
There are also exponential function worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is an exponential function?
An exponential function is is a mathematical function in the form y=ab^x, where x and y are variables, and a and b are constants, b > 0.
For example,
The diagram shows the graphs of y=2^x, \, y=0.4^x, and y=0.5(3^x).
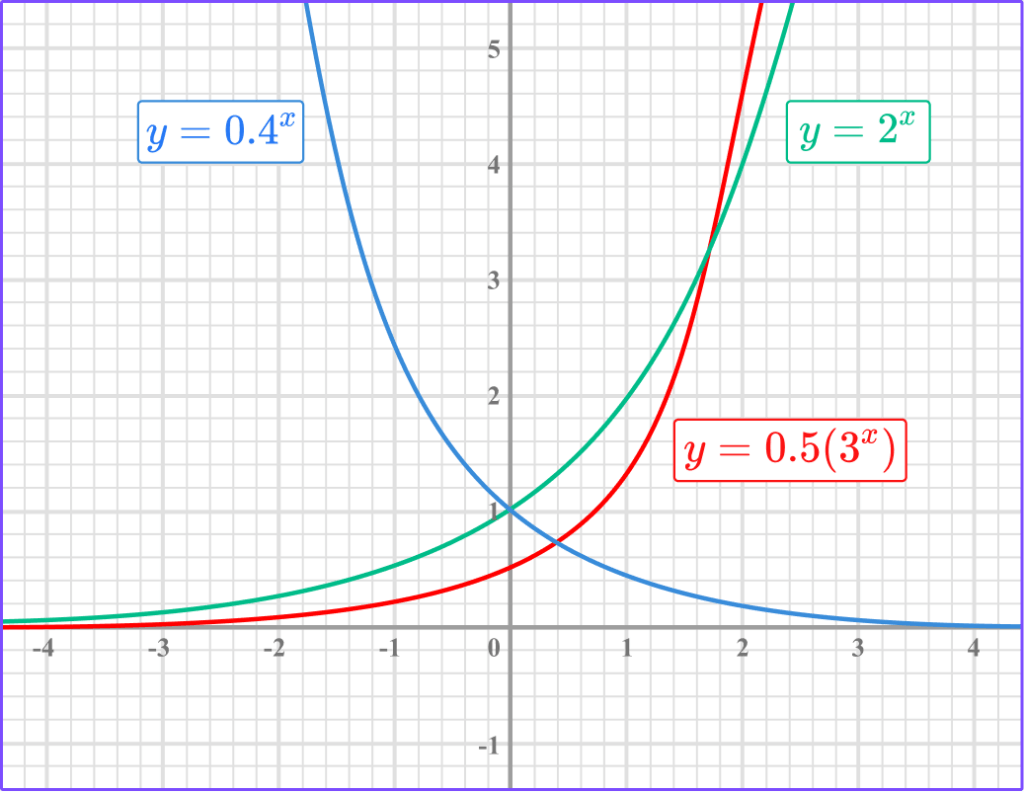
The graph of an exponential function has a horizontal asymptote. These all have a horizontal asymptote at y=0 (the x -axis) because ab^x can never equal zero.
Exponential functions are a very important part of mathematics and can be applied to many real-life situations such as finance, population growth, radioactive decay, and the spread of viruses.
If something is said to have exponential growth or exponential decay, then it can be modelled using an exponential function.
The word “exponent” means index or power. So an equation in the form y=ab^x is called an exponential equation because the variable x is the power in the equation.
A exponential function can also have a negative exponent y=ab^{-x}.
These can be rewritten with a positive exponent using the laws of indices.
For example,
y=4^{-x}
y=(4^{-1})^x
y=\left( \cfrac{1}{4}\right)^x
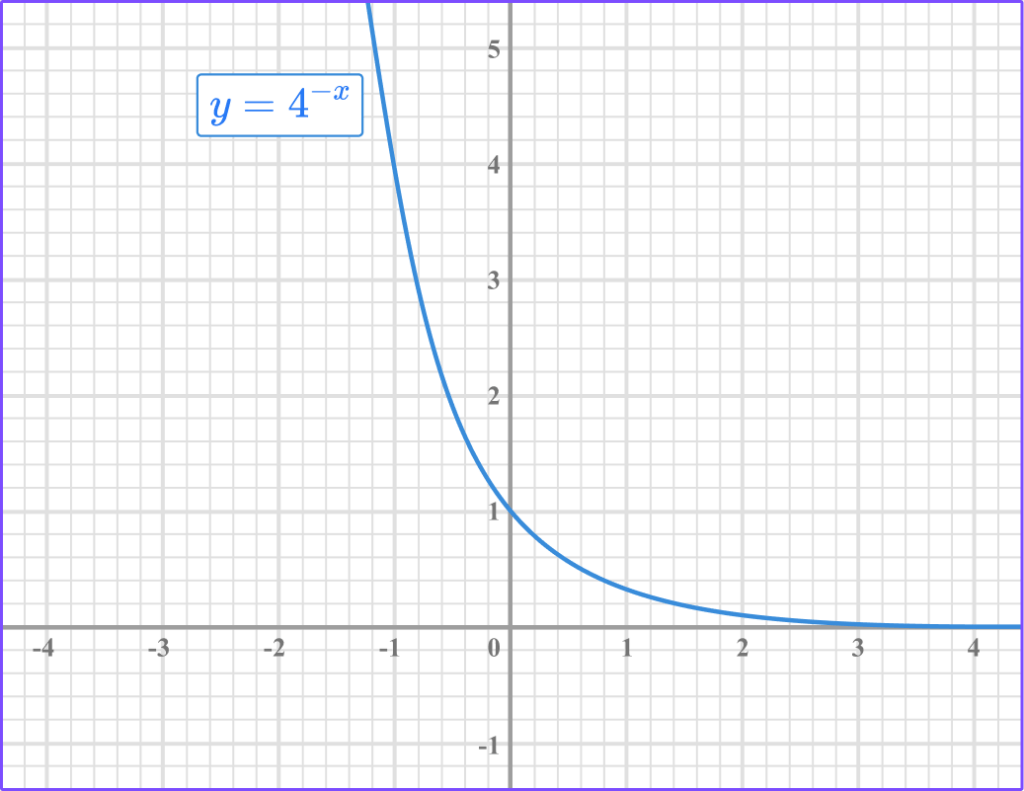
In general,
y=ab^{-x} is the same as y=a\left(\cfrac{1}{b}\right)^x .
Note that b will always be positive.
What is an exponential function?
How to draw exponential graphs
In order to draw exponential graphs:
- Make a table of values for \textbf{x} and calculate the \textbf{y} -values.
- Plot the points on an \textbf{xy} coordinate plane
- Join the points with a smooth curve.
Explain how to draw exponential graphs

Exponential function worksheet
Get your free exponential function worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONExponential function worksheet
Get your free exponential function worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONRelated lessons on functions in algebra
Exponential function is part of our series of lessons to support revision on functions in algebra. You may find it helpful to start with the main functions in algebra lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Drawing exponential graph examples
Example 1: drawing an exponential graph in the form y = ax, a > 1
Draw the graph of y=3^x on the axes provided.
- Make a table of values for \textbf{x} and calculate the \textbf{y} -values.
We have x values from -2 to 3.
We can find the y -values with or without a calculator.
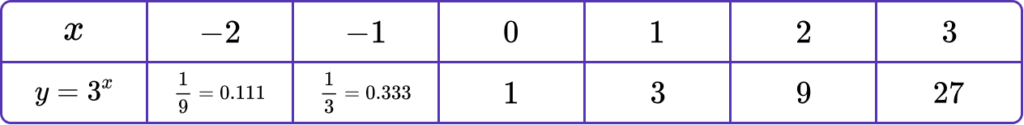
2Plot the points on an \textbf{xy} coordinate plane.
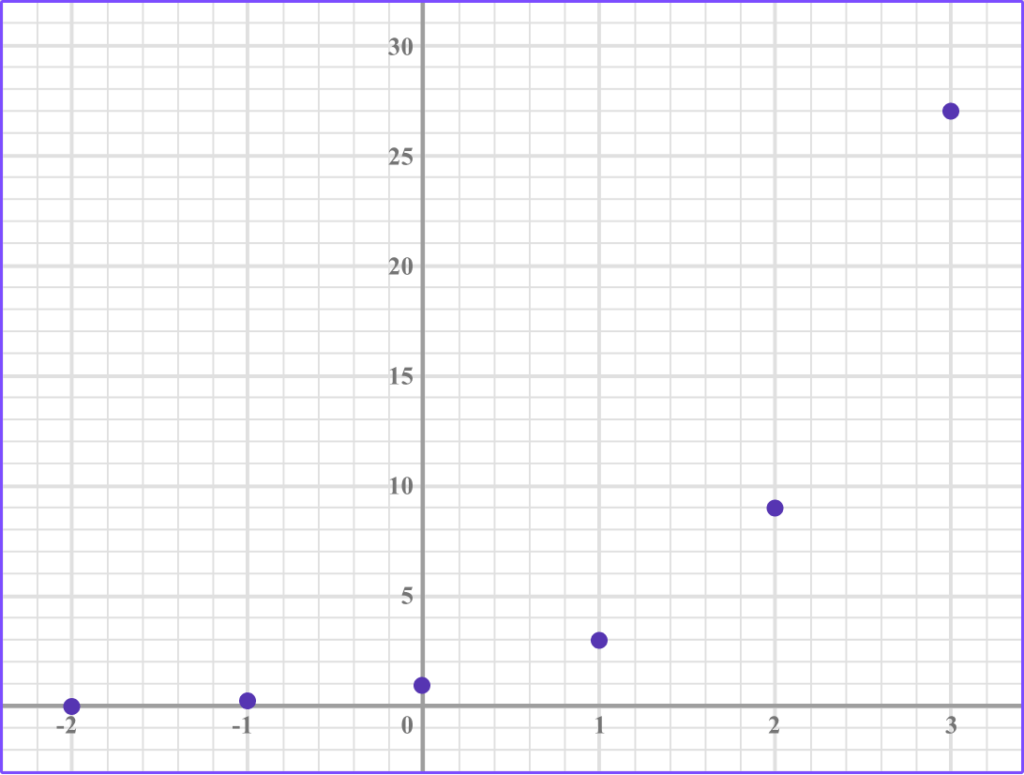
3Join the points with a smooth curve.
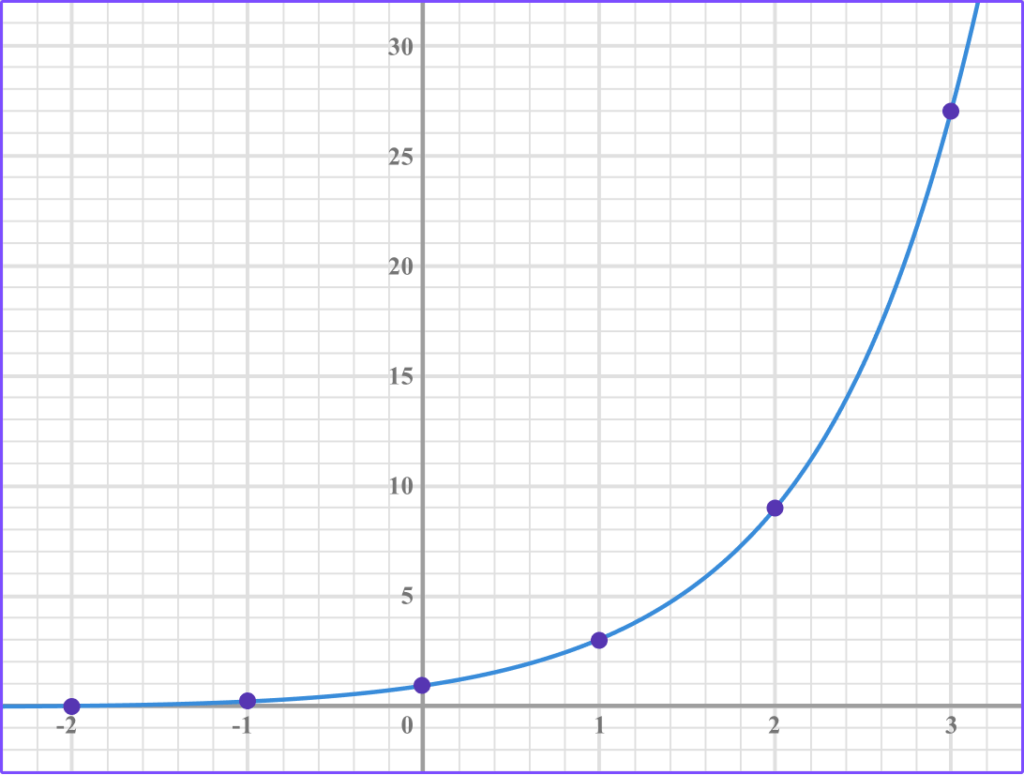
Example 2: drawing an exponential graph in the form y = ax, 0 < a < 1
Draw the graph of y=0.5^x on the axes provided.
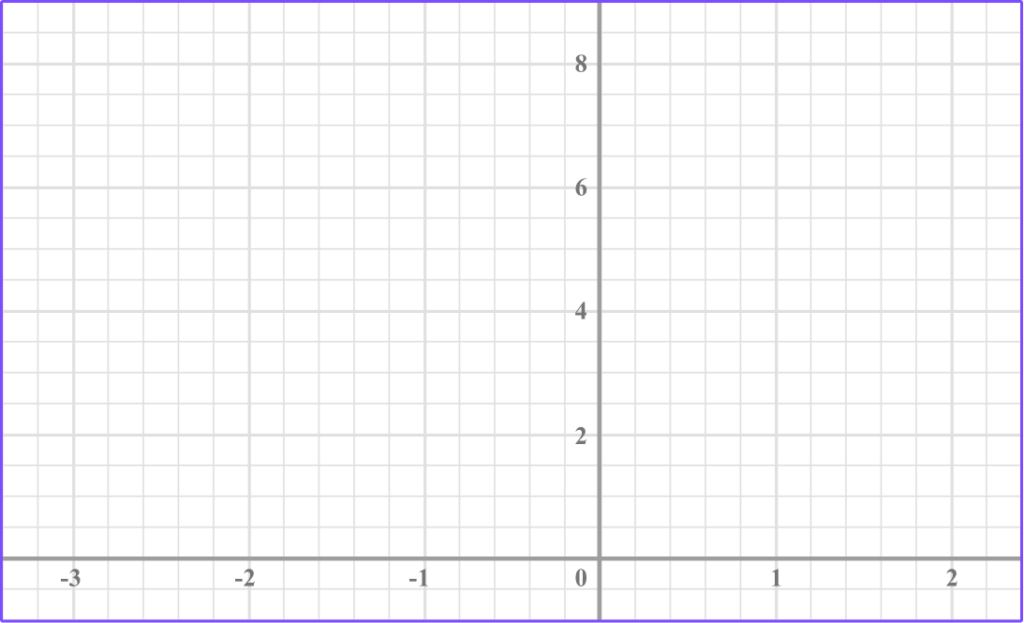
Make a table of values for \textbf{x} and calculate the \textbf{y} -values.
We have x values from -3 to 2.
We can find the y -values with or without a calculator.

Plot the points on an \textbf{xy} coordinate plane.
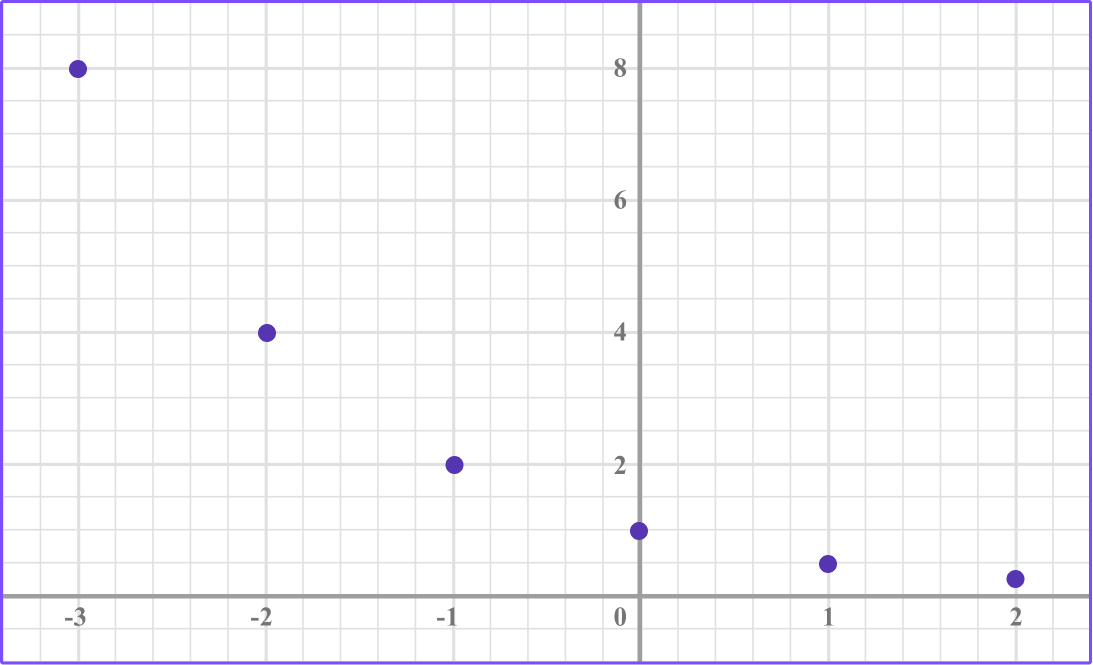
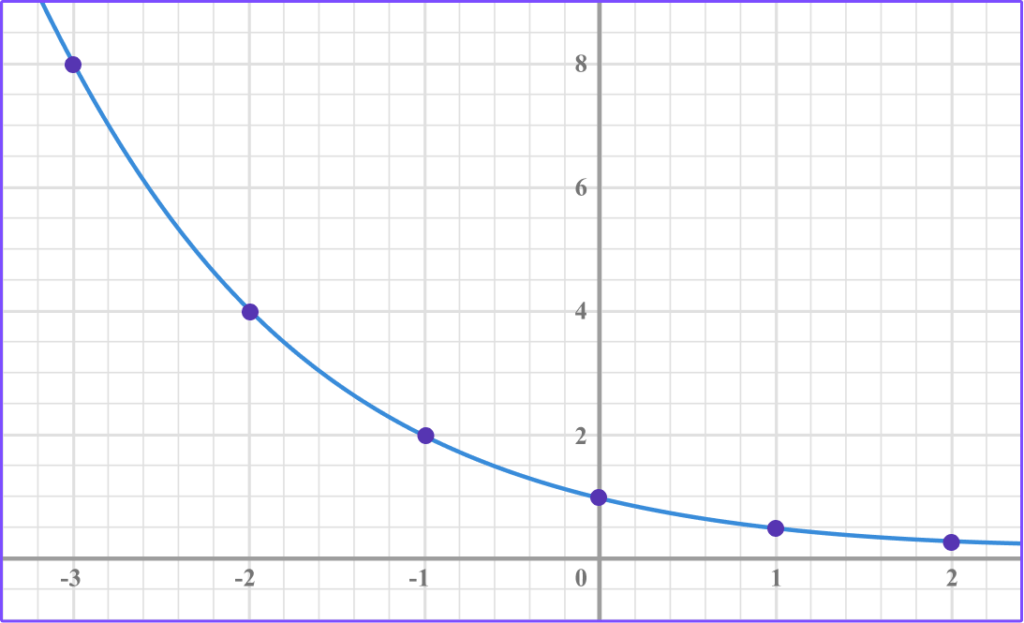
Join the points with a smooth curve.
Example 3: drawing an exponential graph in the form y = abx
Draw the graph of y=0.2(4^x) on the axes provided.
Make a table of values for \textbf{x} and calculate the \textbf{y} -values.
We have x values from -2 to 2.
We can find the y -values with or without a calculator.

Plot the points on an \textbf{xy} coordinate plane.
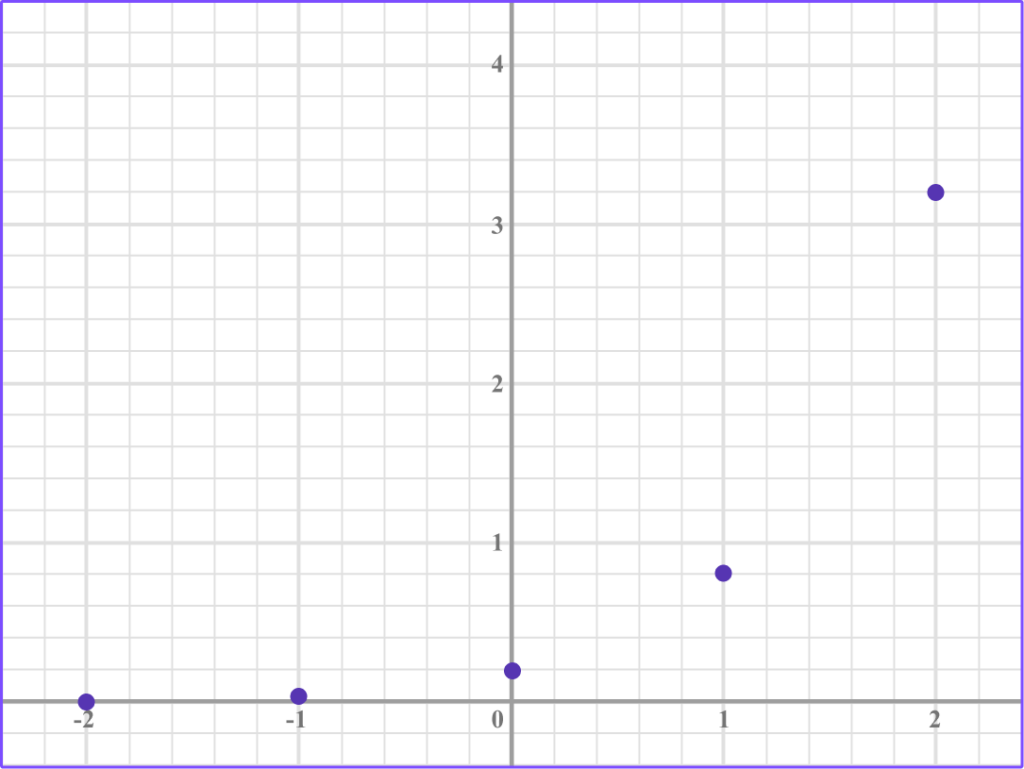
Join the points with a smooth curve.
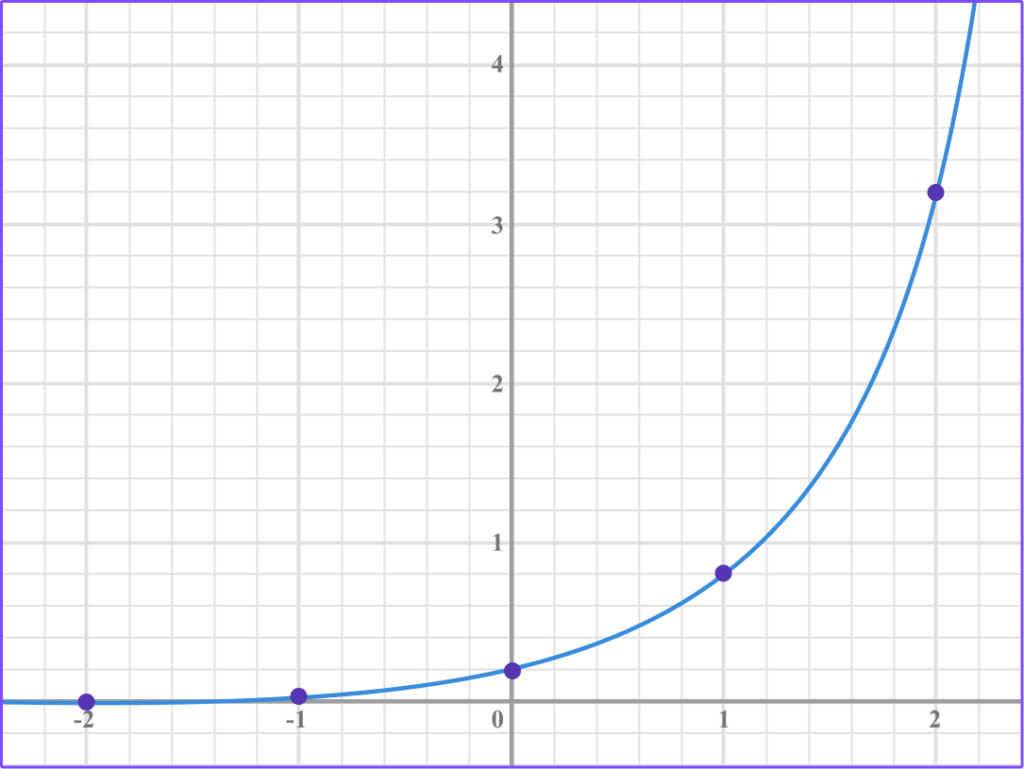
How to find exponential functions
In order to find exponential functions:
- Find two points that lie on the graph.
- Form two equations in the form \bf{y=ab^x}.
- Solve the equations simultaneously.
Explain how to find exponential functions

Finding exponential functions examples
Example 4: finding exponential functions given the y-intercept
Find the equation of the exponential function in the form y=ab^x.
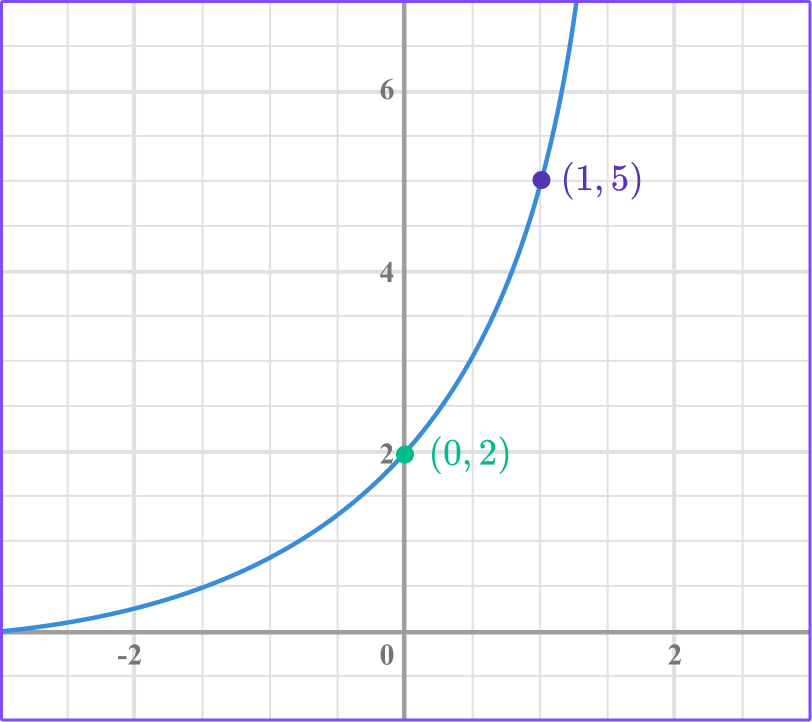
Find two points that lie on the graph.
We have the points (0, 2) and (1, 5).
Form two equations in the form \bf{y=ab^x} .
(0, 2) gives us 2=ab^0.
(1, 5) gives us 5=ab^1.
Solve the equations simultaneously.
We can simplify the two equations before solving.
b^0=1, therefore 2=ab^0 gives us a=2.
b^1=b, therefore 5=ab^1 gives us 5=ab.
We know a=2, therefore
b=2.5 .
The exponential equation is y=2(2.5^x).
Example 5: finding exponential functions by dividing the equations
Find the equation of the exponential function in the form y=ab^x .
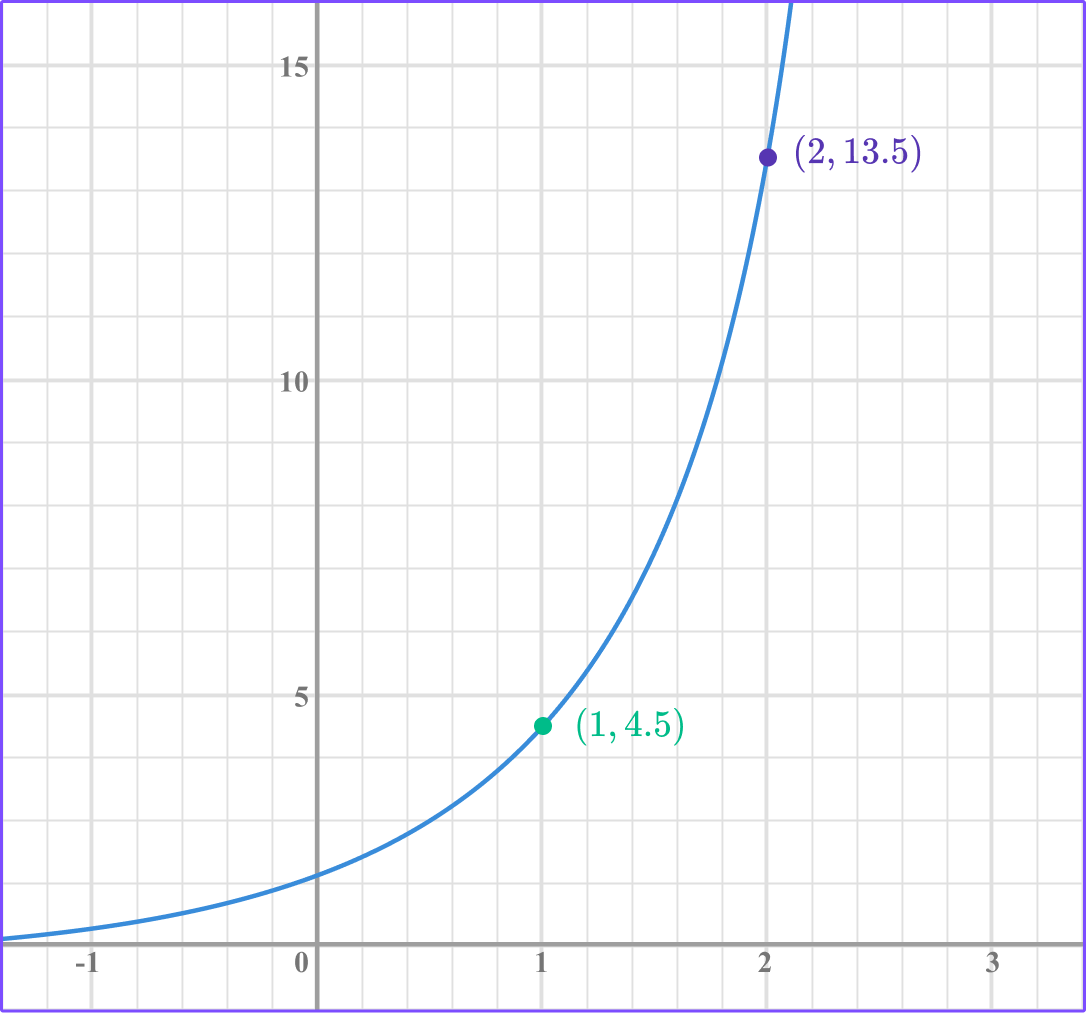
Find two points that lie on the graph.
We have the points (1, 4.5) and (2, 13.5).
Form two equations in the form \bf{y=ab^x} .
(1, 4.5) gives us 4.5=ab.
(2, 13.5) gives us 13.5=ab^{2}.
Solve the equations simultaneously.
We can solve the equations simultaneously by dividing one equation by the other.
\cfrac{13.5}{4.5}=\cfrac{ab^2}{ab}
This gives 3=b.
Substituting this into 4.5=ab gives
4.5=3a
a=1.5
The exponential equation is y=1.5(3^x).
Example 6: finding exponential functions by dividing the equations
Find the equation of the exponential function in the form y=ab^x .
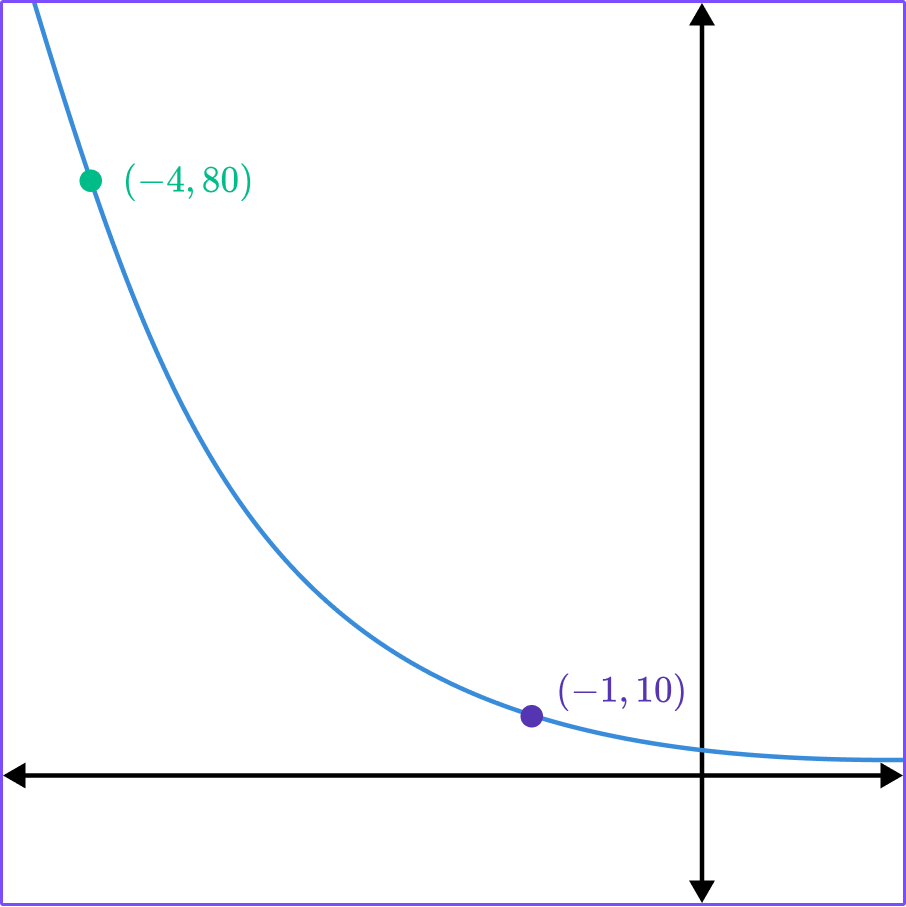
Find two points that lie on the graph.
We have the points (-4, 80) and (-1, 10).
Form two equations in the form \bf{y=ab^x} .
(-4, 80) gives us 80=ab^{-4}.
(-1, 10) gives us 10=ab^{-1}.
Solve the equations simultaneously.
We can solve the equations simultaneously by dividing one equation by the other.
\cfrac{10}{80}=\cfrac{ab^{-1}}{ab^{-4}}
This gives
\cfrac{1}{8}=b^3
\cfrac{1}{2}=b
Substituting this into 10=ab^{-1} gives
10=2a
a=5
The exponential equation is y=5(0.5^x).
Common misconceptions
- Applying the exponent incorrectly
A common error is to confuse y=ab^x with y=(ab)^x. This is especially important when substituting values into a calculator or finding values to plot a graph. y=ab^x means y=a\times (b^x).
- Confusing exponentials with polynomials
Some students can make the mistake of thinking 2^x is the same as x^2 and calculate 2^3 as 9.
Practice exponential function questions
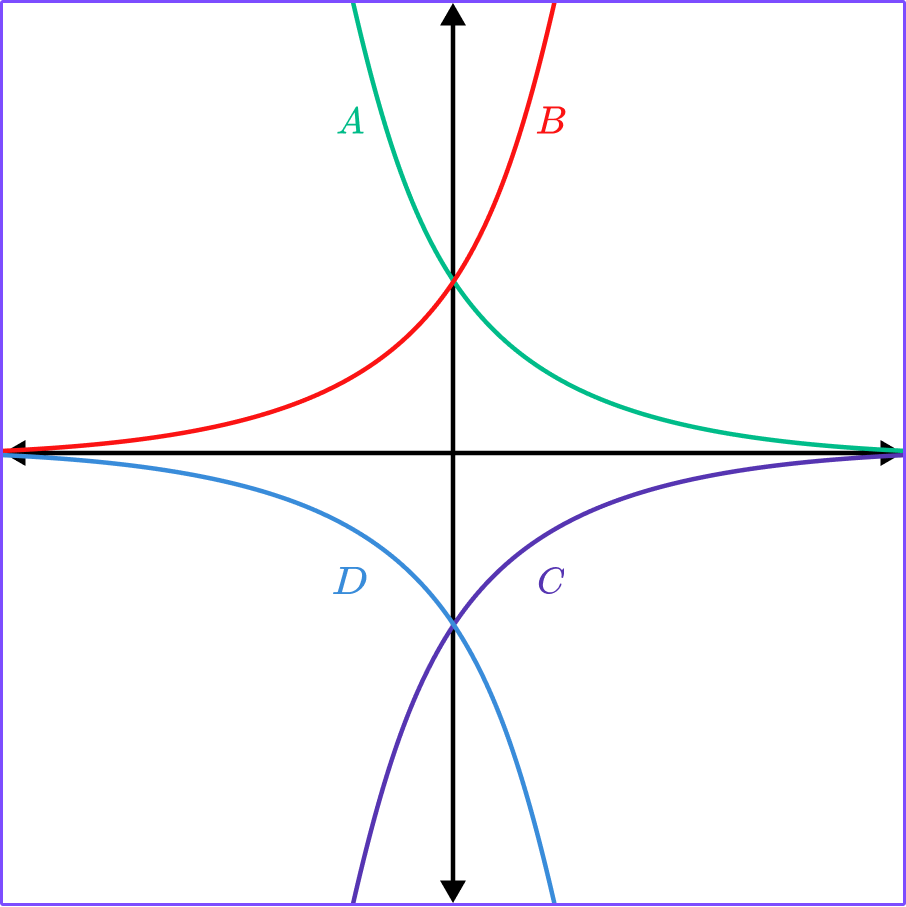
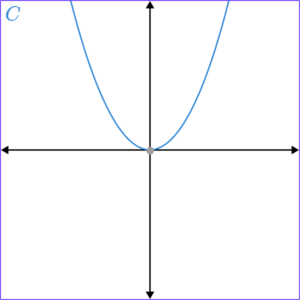
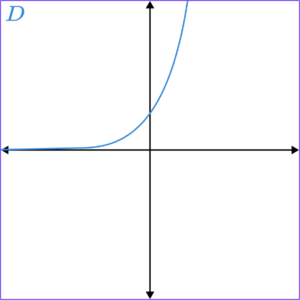
1. Which of the graphs shows y=2^x?
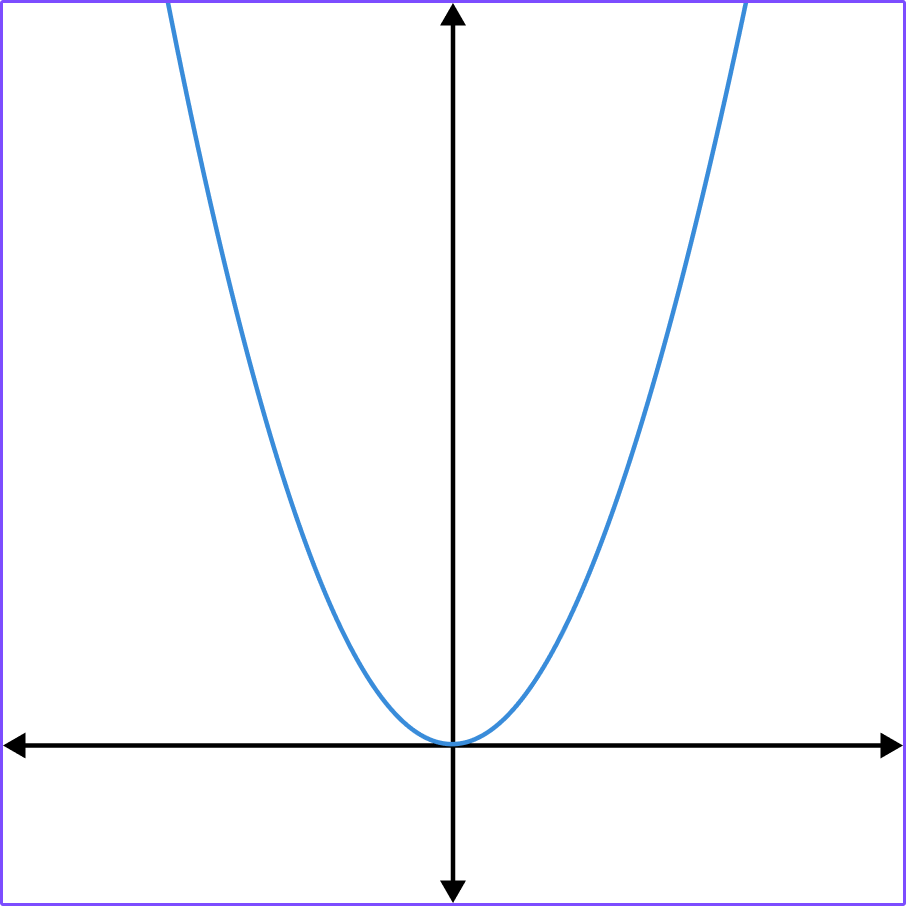

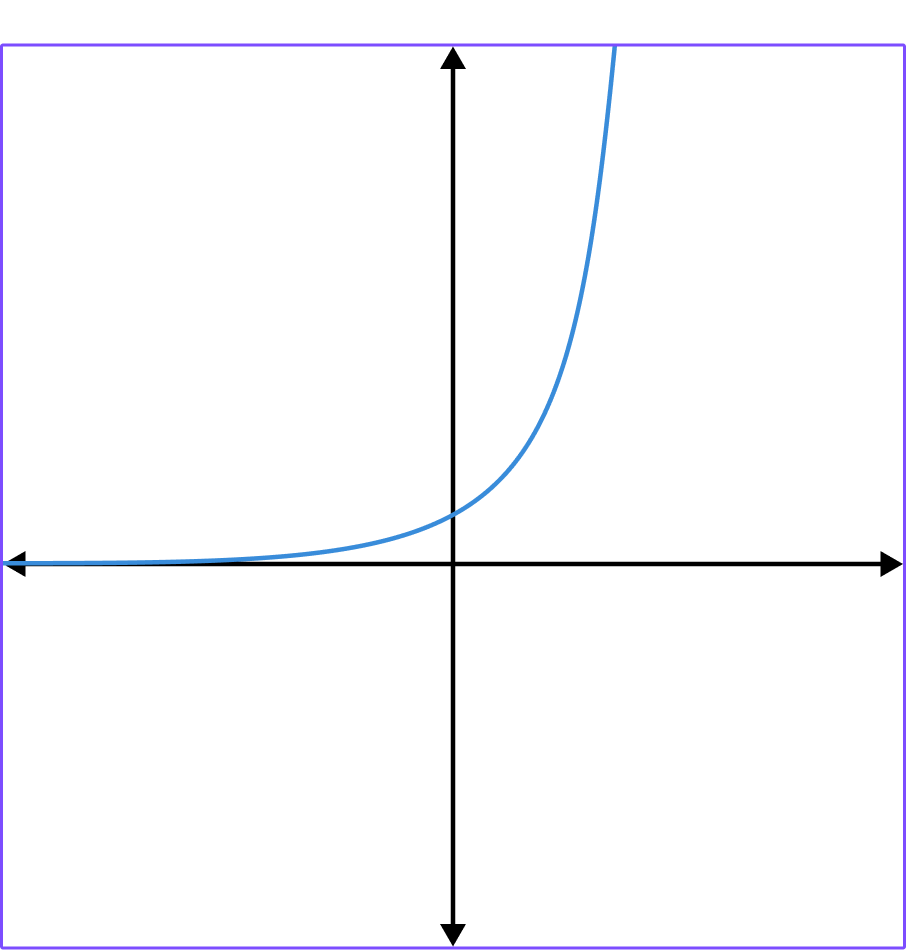

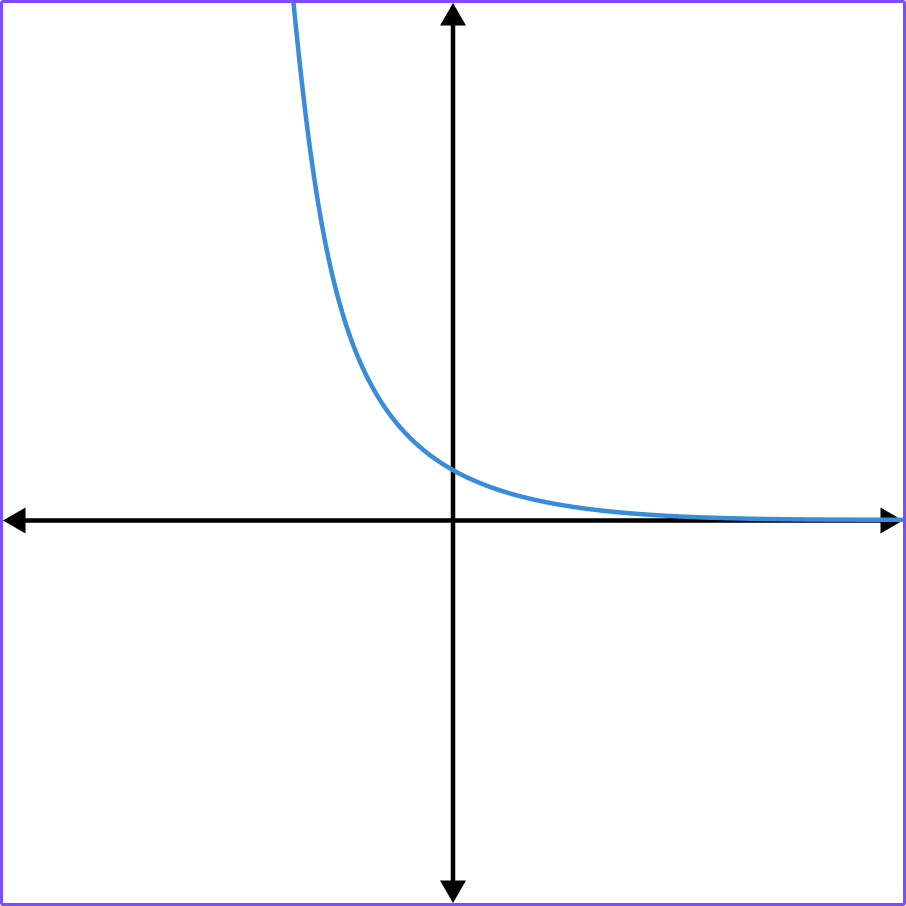

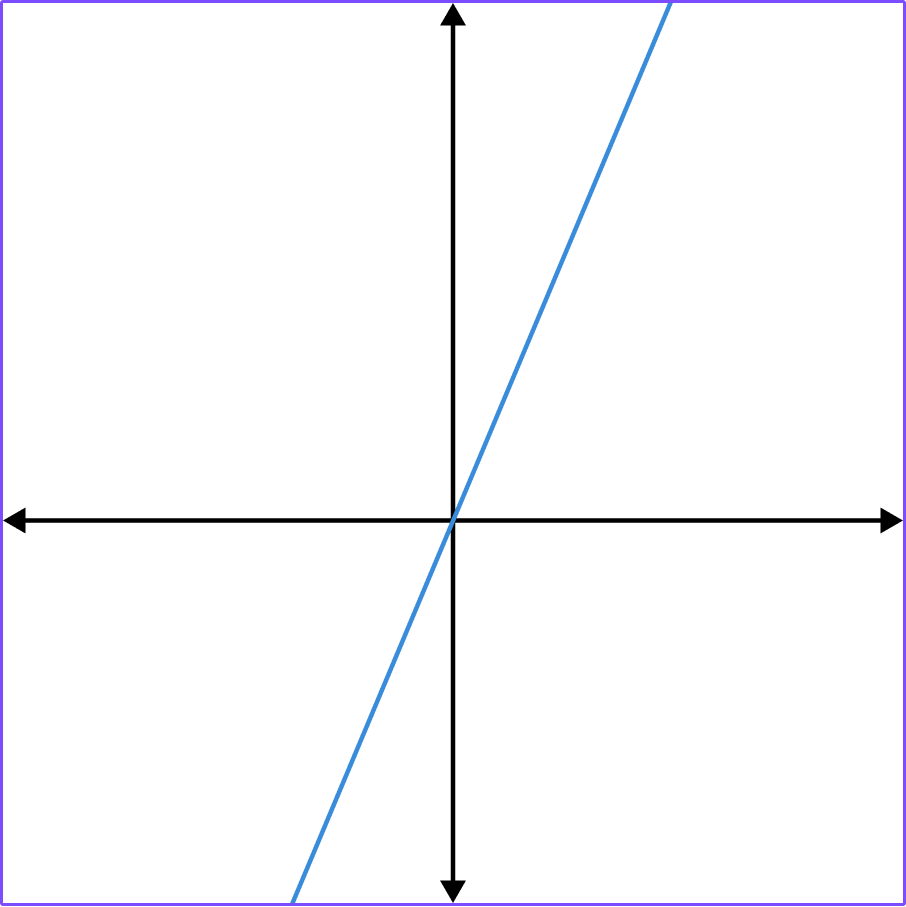

y=2^x has the table of values,

2. Which of the graphs is y=\left(\cfrac{1}{2}\right)^x?
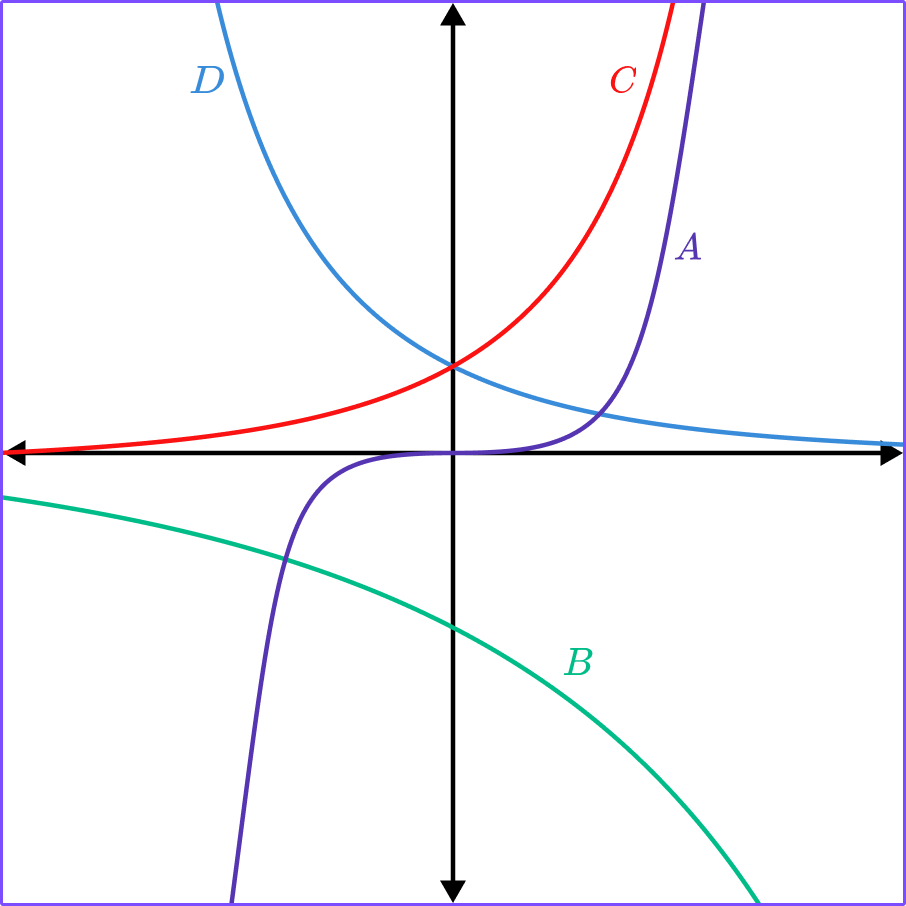
A

B

C

D

y=\bigl(\cfrac{1}{2}\bigr)^x has the table of values,

3. Which of the graphs is y=2\left(3^{-x}\right)?
A

B

C

D

y=2\left(3^{-x}\right) has the table of values,

4. An exponential function goes through the points (0, 1) and (2, 25). What is the function?




Using the points and y=ab^x, \, b>0.
(0, 1) gives 1=a.
(2, 25) gives 25=ab^2.
b^2=25
b=5, because b is always positive.
5. An exponential function goes through the points (0, 3) and (2, 48). What is the function?




Using the points and y=ab^x, \, b>0.
(0, 3) gives 3=a.
(2, 48) gives 48=ab^2.
48=3b^2
b^2=16
b=4, because b is always positive.
6. An exponential function goes through the points (1, 9) and (4, 30.375). What is the function?




Using the points and y=ab^x, \, b>0.
(1, 9) gives 9=ab.
(4, 30.375) gives 30.375=ab^4.
Dividing gives
\begin{aligned} \cfrac{30.375}{9}&= \cfrac{ab^4}{ab} \\\\ 3.375 &= b^3\\\\ b&=1.5 \end{aligned}
Substituting into 9=ab gives
a=6.
Exponential function GCSE questions
1. Match the equations to the graphs.
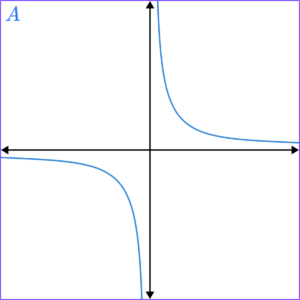
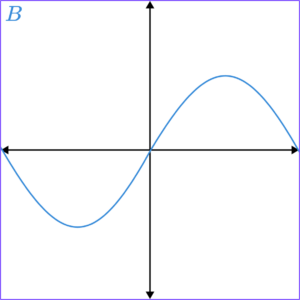

(4 marks)
C
(1)
D
(1)
A
(1)
B
(1)
2. Plot the graph of y= \left(\, \cfrac{1}{4} \, \right)^x, for x values between -1 and 1, on the grid below.
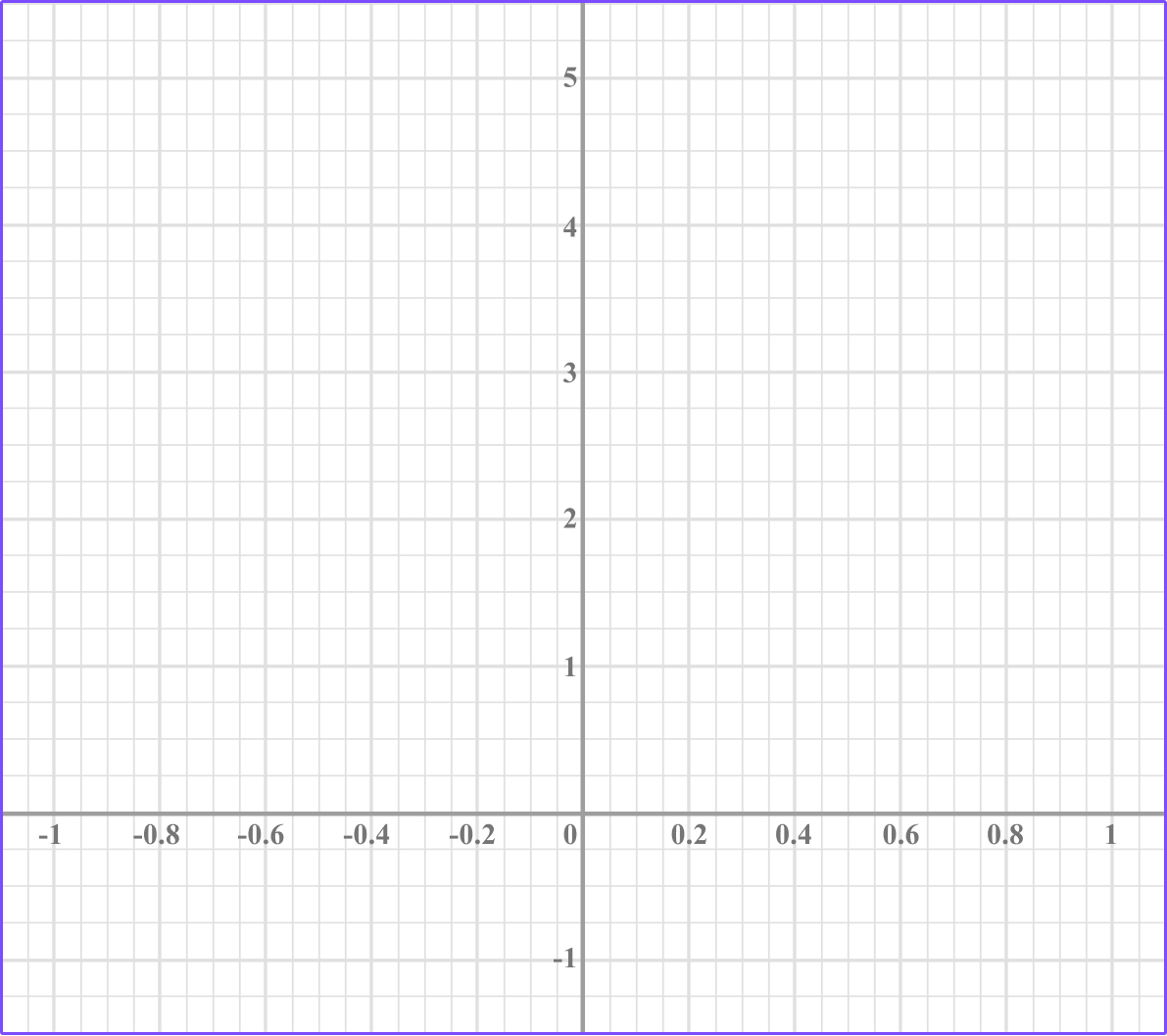
(3 marks)
2 correct points plotted.
(1)
4 correct points plotted.
(1)
Points joined with smooth curve.
(1)
3. An exponential function in the form f(x)=ab^x, \, b>0 , goes through the points (1, 4) and (3, 256). Find the equation of the exponential function f(x).
(4 marks)
Forms equations 4=ab and 256=ab^3.
(1)
Process to divide equations or b^2=64.
(1)
b=8
(1)
a=0.5
(1)
Exponential function links to other topics
We use exponential functions when generating geometric sequences.
The nth term of a geometric sequence is given by u_n=ar^{n-1}. This is an exponential function.
Here is the nth term of a geometric sequence u_n=4(2)^{n-1}.
u_1=4(2)^{0}=4
u_2=4(2)^{1}=8
u_3=4(2)^{2}=16
Step-by-step guide: Geometric sequences
We have also seen exponential functions when generating the amount in a bank account which is receiving compound interest.
The compound interest formula is A=P\left(1+\cfrac{r}{100}\right)^n.
Where,
- A represents the final amount.
- P represents the original principal amount.
- r is the interest rate.
- n represents the number of times the interest rate is applied.
Step-by-step guide: Compound interest
Learning checklist
You have now learned how to:
- Recognise, sketch and interpret graphs of exponential functions y=k^x, for positive values of k
- Recognise the graph of exponential functions
- Be able to find missing values from exponential functions that satisfy given coordinates
The next lessons are
Exponential functions in A level mathematics
Exponential functions are explored in much more depth in A level mathematics.
We learn about a special number e.
e is a very important mathematical constant just like \pi .
e=2.7182818… and is an irrational number whose decimals never recur or terminate.
e is also known as Euler’s number after the Swiss mathematician Leonhard Euler, but it was actually discovered by another Swiss mathematician called Jacob Bernoulli whilst studying compound interest.
y=e^x is known as “the exponential function”.
e has some very special properties.
The value of the derivative of y=e^x is e^x. This means the gradient of the graph of y=e^x at any value x is the same as the value of e^x.
It can also be approximated using the formula \left(1+\cfrac{1}{n} \, \right)^n .
If you use increasing large values for n, the approximation will get closer and closer to e.
The inverse function of exponential functions are called logarithms.
Logarithmic functions have different bases depending on the base of the original exponential function.
The inverse of an exponential function y=2^x would be y=\log_2 x. We say “log base 2 ”.
The inverse of the exponential function y=e^x isn’t written as y=\log_e x but y=\ln x. This is known as the natural logarithm instead of saying “log base e”.
Logarithms are used to solve exponential equations, they can find the time for a bank investment to reach a required value or the half-life of a radioactive compound.
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.