One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Factors and multiples Simplifying expressions Expanding brackets Factorising Types of triangles Types of quadrilaterals Angle rules Angles in polygons VectorsThis topic is relevant for:

Mathematical Proof
Here we will learn about proofs maths, including algebraic proof, proofs of congruence, circle theorem proofs and proofs using vectors.
There are also geometric proof worksheets based on Edexcel, AQA and OCR exam style questions, along with further guidance on where to go next if you’re still stuck.
What is proof maths?
Proof maths is using knowledge of mathematics to prove if a mathematical statement is true. There are two main types of proof that you may need to use at GCSE mathematics.
- Algebraic proof
Here we use algebraic manipulation, such as expanding and factorising expressions, to prove a statement involving integers, a problem involving algebraic terms or an identity.
- Geometric proof
Here we use geometrical reasoning to prove a statement or theorem about a geometry problem. This may involve problems including congruent shapes, congruent triangles, circle theorems and vectors.
What is proof maths?

Mathematical proof worksheet

Get your free mathematical proof worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Mathematical proof worksheet

Get your free mathematical proof worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEAlgebraic proof
Algebraic proof is using algebraic manipulation, such as expanding and factorising expressions, to prove a statement involving integers, a problem involving algebraic terms or an identity.
You need to be able to express mathematical statements using algebraic expressions and then use these expressions in your proof.
For example,
Prove that the product of two odd numbers will always be odd.
First we need to know how to express even and odd numbers algebraically.
Even numbers:
If we want to express an even number we can call it 2n, because all even integers are multiples of 2. A multiple of 3 would be 3n, a multiple of 4 would be 4n etc.
Odd numbers:
The odd numbers are always 1 above or below an even number. So we could call an odd number 2n+1.
For two different odd numbers we can use 2n+1 and 2m+1.
The product of these two odd numbers will be,
\begin{aligned} \left( 2n+1 \right)\left( 2m+1 \right) & \equiv 4nm+2n+2m+1 \\\\ & \equiv 2\left( 2nm+n+m \right)+1 \end{aligned}This is in the form 2n+1 therefore it is always odd.
Step-by-step guide: Prove algebraically
Geometric proof
Geometric proof is using geometrical reasoning to prove a statement or theorem about geometry. This may involve problems including congruent shapes, congruent triangles, circle theorems and vectors.
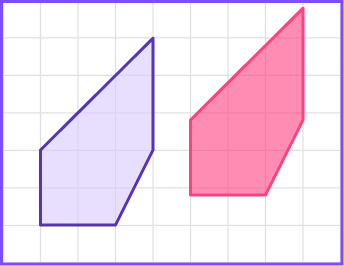
- Congruent shapes are shapes that are exactly the same. The corresponding sides are the same and the corresponding angles are the same.
To determine whether two shapes are congruent, we need to check whether all the angles and all the sides of the shapes are the same. If two shapes are congruent they will fit exactly on top of one another.
For example,
These two polygons are congruent.
Step-by-step guide: Congruent shapes
- Congruent triangles are triangles that are exactly the same size and shape.
There are 4 conditions that can be used to prove congruency in triangles.
- Side-side-side (SSS)

- Right angle, hypotenuse and one other side (RHS)

- Side-angle-side (SAS)

- Angle-side-angle (ASA)
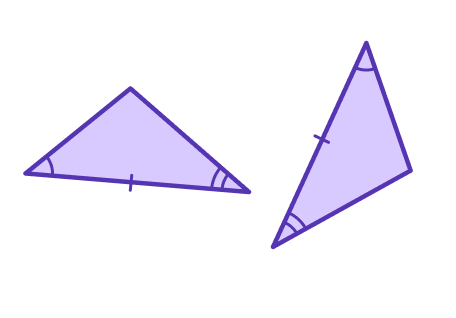
You may be asked to prove that two shapes or two triangles are congruent.
For example,
Below is a parallelogram ABCD.
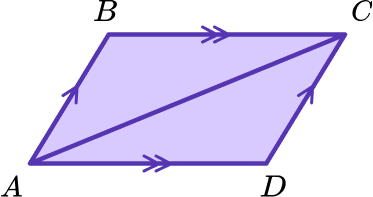
Prove that triangle ABC is congruent to triangle CDA.
This can be done in many ways, so it is important to realise that there is not just one correct answer for this proof. We need to state the reasons and facts that show the triangles are congruent using properties of shapes.
Triangle ABC is congruent to triangle CDA by SSS (we could have also used SAS or ASA to prove they were congruent). The following statements then show that all three sides of the triangles have an equal corresponding side on the other.
AB = CD because opposite sides in a parallelogram are equal in length.
AD = BC because opposite sides in a parallelogram are equal in length.
AC is a common side.
Step-by-step guide: Congruent triangles
- You could be asked to prove one of the circle theorems. Some of the proofs require the use of other circle theorems so it’s important to be familiar with all of the circle theorems and other angle rules.
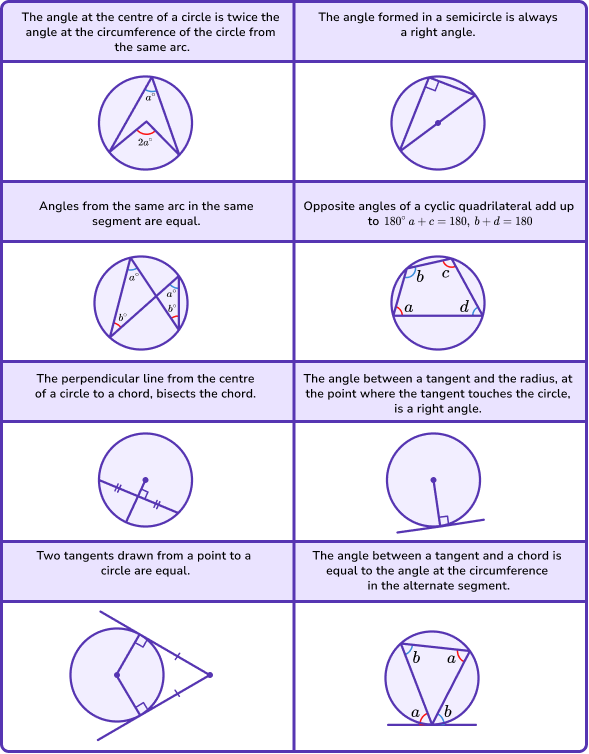
For example,
Prove that opposite angles of a cyclic quadrilateral total 180^{o}.
We need to use the circle theorem, the angle at the centre is twice the angle at the circumference.
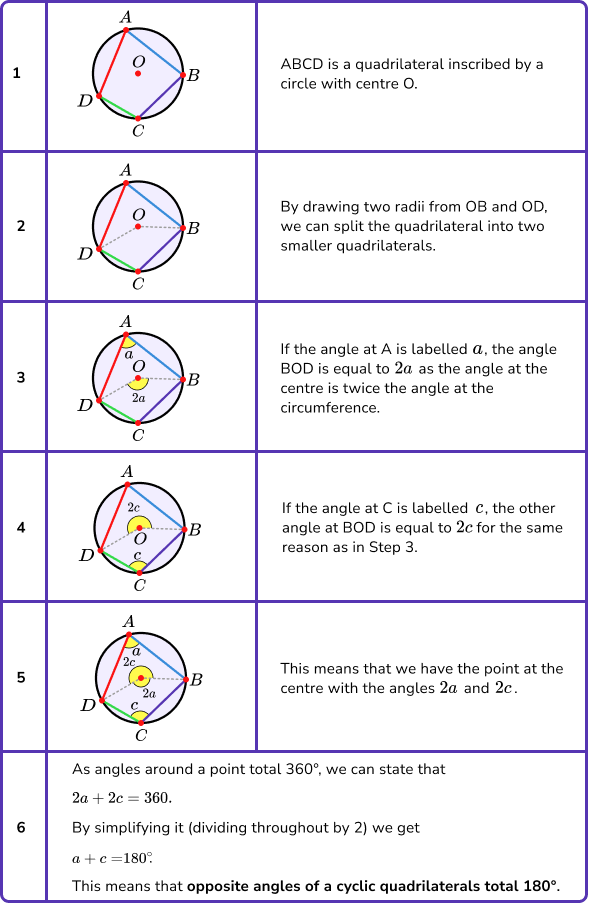
Step-by-step guide: Circle theorems
- In vector questions, you may have to prove that two vectors are parallel or that three points lie in a straight line. To do this you will need to use some key facts about vectors.
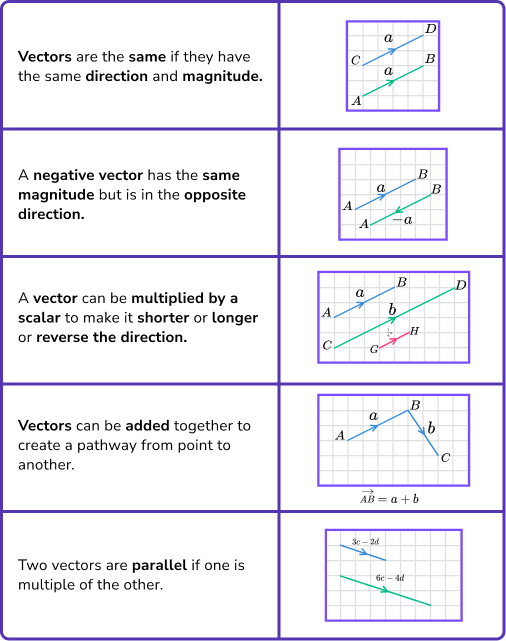
For example,
Below is the trapezium OABC.
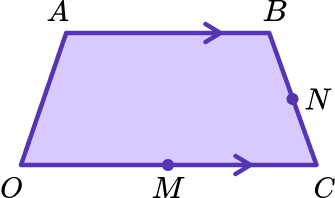
M is the midpoint of OC and N is the midpoint of BC.
Prove that \overrightarrow{MN} is parallel to \overrightarrow{OB}.
Using the information we can find,
\begin{aligned} & \overrightarrow{OC}=3\mathsf{b} \\\\ & \overrightarrow{OB}=\mathsf{a}+2\mathsf{b} \\\\ \end{aligned}This then gives us,
\overrightarrow{BC}=\overrightarrow{BO}\mathsf{+}\overrightarrow{OC}=\mathsf{b}-\mathsf{a}We can then find,
\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OC}=\frac{3}{2}\mathsf{b} \ and \ \overrightarrow{BN}=\frac{1}{2}\overrightarrow{BC}=\frac{1}{2}\mathsf{b}-\frac{1}{2}\mathsf{a}
which then gives us
\overrightarrow{MN}=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{BN}=\frac{1}{2}\mathsf{a}+\mathsf{b=}\frac{1}{2}\overrightarrow{OB}Therefore, \overrightarrow{MN} is parallel to \overrightarrow{OB} because they are multiples of each other.
Step-by-step guide: Vector problems
Other types of proof
There are other questions involving proof that ask you to show something is not true by finding a counterexample.
For example,
John says “if you add one to a multiple of four, you will always get a prime number”
Prove that John is wrong.
We can do a couple of things here. We could try adding one to different multiples of four until we find one that is not prime.
4 + 1 = 5, prime
8 + 1 = 9, not prime
12 + 1 = 13, prime
16 + 1 = 17, prime
We can see that his statement works for some values but does not when we use the 2nd multiple of 4, 8.
We could also generate the arithmetic sequence 4n+1 and see if they are prime.
n=1, \ 4n+1 =5, prime
n=2, \ 4n+1 =9, not prime
n=3, \ 4n+1 =13, prime
n=4, \ 4n+1 =17, prime
We can see that his statement works for some values but does not when n=2.
Further study
In A level Maths and Further Maths, mathematical proof is studied in much greater depth. Some of the methods of proof are
- Proof by contradiction – for example, proving the square roots of prime numbers are irrational numbers by assuming they are rational and showing it cannot happen.
- Proof by exhaustion – proving a statement by trying every possible combination or number.
- Proof by induction – proving statements involving positive integers by showing it is true for one and then true for consecutive integers.
Common misconceptions
- Incorrect expression for odd and even integers
A common mistake is to write n and n+1 for even and odd integers. It is important to remember that even numbers are multiples of 2 \ (2n) and odd numbers are an even number plus or minus any odd number (2n-1).
- Shapes can be congruent but in different orientations
The second shape may be in a different orientation to the first shape. The shapes can still be congruent. Use tracing paper to help you check.
- Shapes can be congruent but mirror images
The second shape may be a mirror image of the first shape. The shapes can still be congruent. Perhaps use tracing paper to help you check.
- AAA – all three angles
AAA – all three angles being equal is NOT a condition for triangle congruence.
These two triangles have identical angles, but the second triangle is an enlargement of the first triangle.
They are similar triangles NOT congruent triangles.
Practice proofs maths questions
1. What could be the correct expressions for two consecutive odd numbers for any value of n?




An odd number can be written as 2n-1. The next odd number will be 2 more.
2. Which of the following conditions can not be used to prove triangles are congruent?




AAA would show triangles are similar but not necessarily congruent.
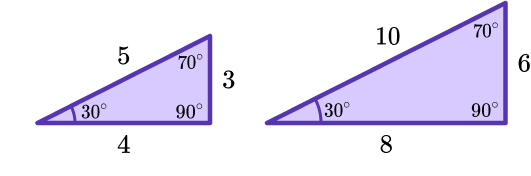
3. Which condition would be the quickest one to use to prove these two triangles are congruent?
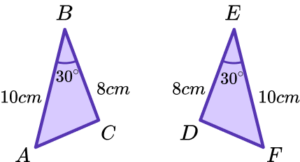




All of the information is provided to show they are congruent by SAS. Other methods would involve calculations of missing sides or angles.
4. What would be a sensible first step to prove the angle at the centre of a circle is twice the angle at the circumference?
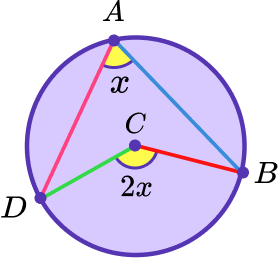
Draw a line from D to B.

Draw a line from A to C.

Draw a tangent to the circle at B.

Add an extra point E on the circumference and make a cyclic quadrilateral.

Drawing a line from A to C will form two isosceles triangles. The angles in these isosceles triangles will help prove the theorem.
5. What would be the correct method to show that the line OEF is straight?
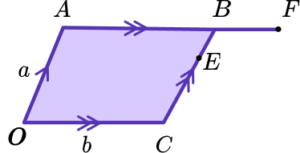
Show \overrightarrow{OB} is parallel to \overrightarrow{EF}.

Show \overrightarrow{OB} is not parallel to \overrightarrow{OF}.

Find two of the vectors \overrightarrow{OE}, \ \overrightarrow{OF}, \ \overrightarrow{EF}, show they are parallel and share a common point.

Find \overrightarrow{EF}.

If two vectors are parallel and share a common point, they must form a straight line.
6. Charlie says, “the expression n^{2}+3n-7 will never give a multiple of 7, when n is an integer”. What counterexample value of n could be used to disprove his statement?




7^{2}+3(7)-7=63, which is a multiple of 7.
Proofs maths GCSE questions
1. The diagram shows a regular pentagon ABCDE.
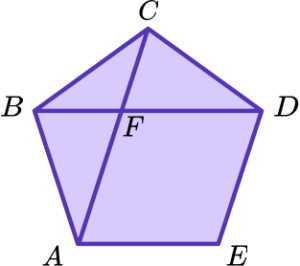
Prove that triangle ABF is congruent to triangle DCF.
(4 marks)
Statement about a corresponding side. For example, AB = DC.
(1)
Statement about a corresponding angle with reason. For example, angle AFB = DFC vertically opposite angles are equal, or angle FBA = angle FCD = 72^{o}.
(1)
Statement about another corresponding side or angle. For example, FAB = angle, FDC = 36^{o}.
(1)
Correct condition given that matches given statements. For example, ASA.
(1)
2. (a) Prove that the product of two even numbers is a multiple of 4.
(b) Prove that the square of a positive integer plus double the same integer plus one gives another square number.
(4 marks)
(a)
2 different even numbers given as 2n and 2m and product attempted.
(1)
Product of 4mn and a statement of multiple of 4 given.
(1)
(b)
n^{2}+2n+1
(1)
(n+1)^2(1)
3. The diagram shows triangle OAB.
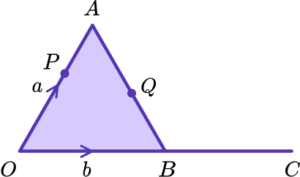
OBC is a straight line with OB = BC.
Q is the midpoint of AB.
OP:PA = 2:1
\overrightarrow{OA} = a, \ \overrightarrow{OB} = b
Prove that PQC is a straight line.
(5 marks)
(1)
\overrightarrow{QB} =\frac{1}{2}b-\frac{1}{2}a(1)
\overrightarrow{QC} =\frac{3}{2}b-\frac{1}{2}a(1)
\overrightarrow{PC} =2b-\frac{2}{3}a(1)
Statement about \overrightarrow{PC} parallel to \overrightarrow{QC}
e.g \overrightarrow{PC} = \frac{4}{3}\overrightarrow{QC} and common point therefore line PQC is straight.
(1)
Learning checklist
You have now learned how to:
- Use algebra to support and construct arguments and proofs
- Apply and prove the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results
- Apply the concepts of congruence and similarity, including the relationships between lengths
- Use vectors to construct geometric arguments and proofs
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.