What Are Equivalent Fractions? Explained For Primary School

Equivalent fractions come up a lot in KS2 maths and some children, parents, and even teachers at primary school can be a little unsure as to what they are and how to find them. This article aims to make things a little clearer.

What are equivalent fractions?

Equivalent fractions are two or more fractions that are all equal even though they have different numerators and denominators. For example, the fraction \frac{1}{2} is equivalent to (or the same as) \frac{25}{50}or \frac{500}{1000}.

Each time the fraction in its simplest form is ‘one half’.

Remember, a fraction is a part of a whole: the denominator (bottom number) represents how many equal parts the whole is split into; the numerator (top number) represents the amount of those parts.

To understand equivalent fractions, make sure you know the basics of fractions

If the concept of equivalent fractions already sounds a bit confusing and you’re not yet clear on what the difference is between whole numbers, denominators of a fraction and different numerators you may want to loop back to our fractions for kids article.

This breaks down the first fraction steps that Key Stage 1 and Key Stage 2 children must take at school, together with clear examples of how to find the value of a fraction using concrete resources, maths manipulatives, pictorial representations and number lines; the difference between unit fractions and non unit fractions; all the way up to proper and improper fractions.

It’s been written as a guide for children and parents to work through together in clear digestible chunks.

Examples of equivalent fractions

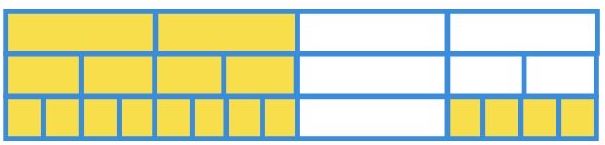
Here are some examples of equivalent fractions using a bar model and showing the ‘parts’ each numerator is referring to out of the ‘whole’ ie the denominator.

\frac{4}{6} = four out of six parts, also shown as a :

Although \frac{8}{12} may look like a different fraction, it is actually equivalent to \frac{4}{6} because eight out of 12 parts is the same as four out of six parts, as shown below:

\frac{2}{3}, or two out of three, is another fraction equivalent to both \frac{4}{6} and \frac{8}{12}.

The three fractions \frac{2}{3}, \frac{4}{6} and \frac{8}{12} are shown below respectively in a fraction wall to demonstrate their equivalence.

How to work out equivalent fractions

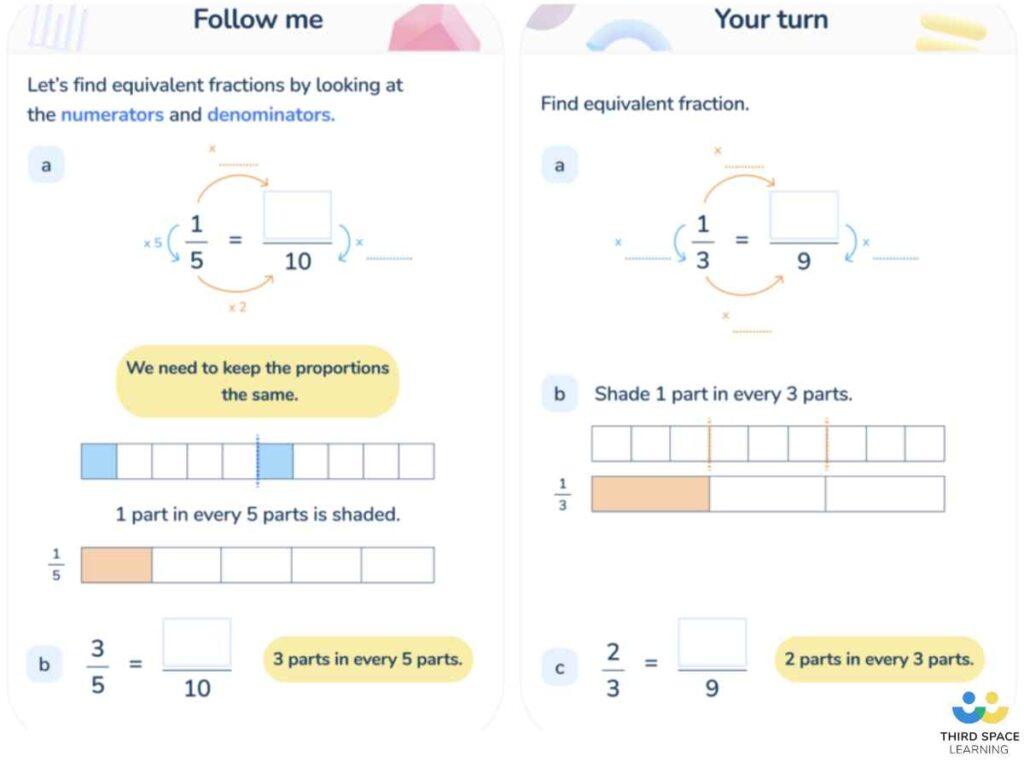
To work out equivalent fractions, both the numerator and denominator of a fraction must be multiplied by the same number. What this means is in fact you’re multiplying by 1, and we know that multiplying by 1 doesn’t change the original number so the fraction will be equivalent.

For example, you can multiply by \frac{2}{2} or \frac{6}{6} and you’re still multiplying by 1.

Equivalent fractions to \frac{3}{5}

\frac{3}{5} x \frac{2}{2} = \frac{6}{10}

\frac{3}{5} x \frac{3}{3} = \frac{9}{15}

\frac{3}{5} x \frac{4}{4} = \frac{12}{20}

So, \frac{3}{5} = \frac{6}{10} = \frac{9}{15} = \frac{12}{20}.

Another way to find equivalent fractions is to divide both the numerator and the denominator of the fraction by the same number – this is called simplifying fractions because both the numerator and denominator digits will get smaller.

For example, to simplify the fraction \frac{9}{12}, find a number that both the numerator and denominator can be divided by (also known as a ‘common factor’), such as 3.

\frac{9}{12} ÷ \frac{3}{3} = \frac{3}{4}, so \frac{9}{12} and \frac{3}{4} are equivalent fractions, with \frac{3}{4} being the fraction in its simplest form.

When do children learn about equivalent fractions in primary school?

Equivalent fractions KS2

The concept of equivalent fractions isn’t introduced until Year 3, where children recognise and show, using diagrams, equivalent fractions with small denominators.

In Year 4, they will recognise and show, using diagrams, families of common equivalent fractions. The National Curriculum’s non-statutory guidance also advises that pupils use factors and multiples to recognise equivalent fractions and simplify where appropriate (for example, \frac{6}{9} = \frac{2}{3} or \frac{1}{4} = \frac{2}{8}).

In Year 5, pupils are taught to identify, name and write equivalent fractions of a given fraction, represented visually, including tenths and hundredths.

In Year 6, they will begin learning how to add fractions and subtracting fractions with different denominators and mixed numbers, using the concept of equivalent fractions. Non-statutory guidance for Year 6 suggests that common factors can be related to finding equivalent fractions and that children practise fraction questions for calculations with simple fractions… including listing equivalent fractions to identify fractions with common denominators.

How do equivalent fractions relate to other areas of maths?

Children will need to have a strong knowledge of equivalent fractions to be able to convert between fractions, decimals and percentages. Knowledge of times tables, the lowest common multiple and highest common factor are also important for equivalent fractions

Wondering about how to explain other key maths vocabulary to your children? Check out our Primary Maths Dictionary, or try these other terms related to equivalent fractions:

• What Is A Unit Fraction?
• What Is BODMAS (and BIDMAS)?
• Properties of shape
• What are 2D shapes?
• What are 3D shapes?

Equivalent fractions questions

1. Write the missing values: \frac{3}{4} = \frac{9}{?} = \frac{?}{24}

(Answer: 12, 18)

2. Circle the two fractions that have the same value:

\frac{2}{10} \frac{1}{3} \frac{1}{2} \frac{5}{10} \frac{1}{4}

(Answer: \frac{1}{2} and \frac{5}{10})

3. Tick two shapes that have \frac{3}{4} shaded.

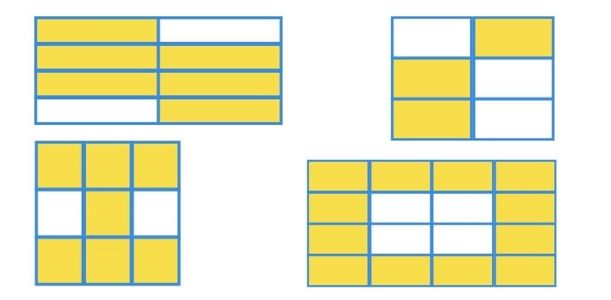
(Answer: top left (\frac{6}{8}) and bottom right (\frac{12}{16}) as both = \frac{3}{4})

4. Shade \frac{1}{4} of this shape.

(Answer: Any 9 triangles shaded)

5. Ahmed says, ‘One-third of this shape is shaded.’ Is he correct? Explain how you know.

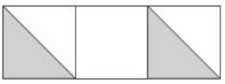
(Answer: Yes – it would be \frac{2}{6} (imagine the middle square split into halves too) which = \frac{1}{3})

Further reading:

• 10 Fun, Simple Fraction Games For KS1 & KS2
• How to Simplify Fractions: A Primary School Guide
• How To Divide Fractions: Step By Step Guide

Equivalent fractions resources

If you’re looking for more equivalent fractions worksheets and maths resources, visit the Third Space Learning Maths Hub. Also download for free:

• Year 3 Equivalent Fractions Worksheet
• Year 6 Equivalent Fractions, Decimals and Percentages Worksheet
• Tarsia Puzzle Equivalent Fractions and Decimals (Year 5)
• Printable Maths Resources Fraction Walls