What Is Variation Theory? A Guide For Primary Maths Teachers
This blog will look at the concept of Variation Theory and attempt to demystify the confusing language surrounding it. It is hoped that this will make Variation Theory an accessible and exciting tool that you can begin to use in your maths lessons, or give you an understanding of what is happening if you recognise the principles, despite never having heard of Variation Theory before!
- What is Variation Theory in primary maths?
- Origins of Variation Theory
- What are the types of Variation Theory?
- What is procedural variation in maths?
- What is conceptual variation in maths?
- Examples and non-examples of Variation Theory
- Standard and non-standard in Variation Theory
- Procedural variation: what’s the same, what’s different and what do you notice?
- Variation Theory worked examples
- Variation Theory FAQs
If you are a premium member of Third Space Learning, you can access a whole-school CPD presentation that covers these points in our Maths Hub.
What is Variation Theory in primary maths?
Variation Theory is a general theory of learning that is used predominantly in mathematics teaching and pedagogy. It emphasises a concept’s essential features by focusing on what is kept the same and what changes, which offers the opportunity to make meaningful connections.
FREE Crib Sheet for Primary School Staff Meetings
Download the key findings from Clare Sealy's 'How I Wish I Taught Maths' research that we think every primary maths teacher should know.
Download Free Now!Origins of Variation Theory
The study of Variation Theory arises mainly from work across two groups of researchers who arrived at similar, but not exactly the same conclusions.
One was Swedish researcher Ference Marton and colleagues who worked on the concept of Variation Theory; the other was Gu Ling Yuan and his team in Shanghai who called it Bianchi (teaching with variation). As one would expect, the emergence of two similar theories has caused confusion in some areas of the sector. In the context of the United Kingdom, the distinction between them is rarely made and so aspects of Bianchi are used under Variation Theory.
They both agree that ‘the central idea of teaching with variation is to highlight the essential features of the concepts through varying the non-essential features’. (Gu, Huang & Marton, 2004). This blog will mainly draw on the learning study of Gu and his team.
The application of Variation Theory is much wider than just the domain of mathematics teaching, but rather as a theory that underpins how students learn anything. The principle that underpins the theory is that new learning occurs when they understand how a critical aspect of a new concept changes (varies) against something that does not change (invariance).
By adjusting their perception of what has remained the same and what has changed, students are more likely to learn the object of learning and understand the underlying mathematical structures being studied. In other words, it is when an educator carefully constructs questions, considers the order in which they appear, and brings the thinking process between questions to the forefront for the students, so that meaningful connections to the mathematical structures can be made from the task.
It is unlikely that a worksheet on its own will bring about the required cognitive process in students needed to benefit from the advantages that Variation Theory offers students in their conceptualisation of mathematical structures.
Do not be deceived into purchasing paid resources that promise to bring about Variation Theory with just a worksheet, unless you can specifically identify how those questions enact the principles of the object of learning, and you feel confident that you can bring out these mathematical structures to the students through your questioning in a very deliberate way.
Indeed, as you will see through some examples, attempts at Variation Theory through only a worksheet approach and no dialogue risk students learning less than not trying to use Variation Theory.
What are the types of Variation Theory?
There are two types of Variation Theory; conceptual variation and procedural variation.

What is procedural variation in maths?
Procedural variation is a process for the formation of mathematical ideas stage by stage, in which students’ experience in solving problems is manifested by the richness of varying problems and the variety of transferring strategies.
It is derived from three parts:
- Varying the problem
- Multiple methods for solving a problem
- Multiple applications of a method to similar problems
As with conceptual variation, the key to success is to teach students to look for connections within the mathematical structures from an early age.
What is conceptual variation in maths?
Conceptual variation is a process that looks at providing students with multiple perspectives and experiences within a given concept or object of learning. It refers to the strategies a teacher may employ to bring to the forefront critical aspects of the desired learning outcome, and increase their understanding by demonstrating it from different perspectives.
Marton and his team of researchers concluded that students notice difference between different objects of learning before they notice sameness.
When employing conceptual variation pedagogy in classroom discourse, it is best to provide examples that are totally different before looking at examples that are similar. For example, if you wanted to demonstrate to students what a triangle was, it would be best to present a triangle along with other shapes that are not triangles to help students distinguish what it is that makes a triangle.
Is this an elephant?
A common non-mathematical approach to explain this is to look at the animal kingdom.

How is it that we are acutely aware of what an elephant is? We are able to distinguish it quite easily from the countless other members of the animal kingdom. If pressed to answer how we know the picture above is an elephant, the first two features that people describe to explain their certainty are the trunk and tusks.

To which my reply is this: is this therefore NOT an elephant?
Clearly, it is. But this is a tuskless elephant, and tusks are one of the distinguishing features of an elephant that many people claim. Perhaps we could go on to explain that the size of an elephant is a distinguishable feature, or the grey colour. An elephant must be grey, have a trunk, be big, and can have tusks, but this is not a requirement.

My reply is: if that is the case, is this an elephant?
Patently it is. Yet, this is hardly a big animal and so would not meet the conditions placed upon it to characterise it as an elephant from above. Therefore, an elephant can be large or small, have tusks or not have tusks, be grey and have a trunk. The necessary conditions of what constitute an elephant become ever clearer.

We also know, instinctively, that this picture is not an elephant despite it being small, grey and not having tusks. We know it cannot be because of the ears, the shape of the head and the lack of trunk. And here, through our visual perception, the idea of Variation Theory comes to life.
By seeing what it is to be something in as many different forms as possible and in forms that are related, be it closely or otherwise, we are able to see that concept from multiple perspectives and experiences to truly know it. At its most basic level, this is conceptual variation.
Examples and non-examples of Variation Theory
As mentioned above, we tend to recognise sameness before we recognise difference. It is from this principle that we can consider introducing critical aspects of mathematical structures through examples and non-examples that we share with students. In this instance, to remain true to Marton’s findings, the examples that demonstrate the critical object of learning that we want students to learn will be invariant, but the background in which we teach will vary. Subsequently, when we show non-examples they act, as one might imagine, to define what the critical aspect is not.
For example, if teaching the meaning of the equals sign, you could have examples of different calculations using all four operations where the answer was correct and examples using all four operations where the answers were incorrect and so the equivalence sign could not be used.
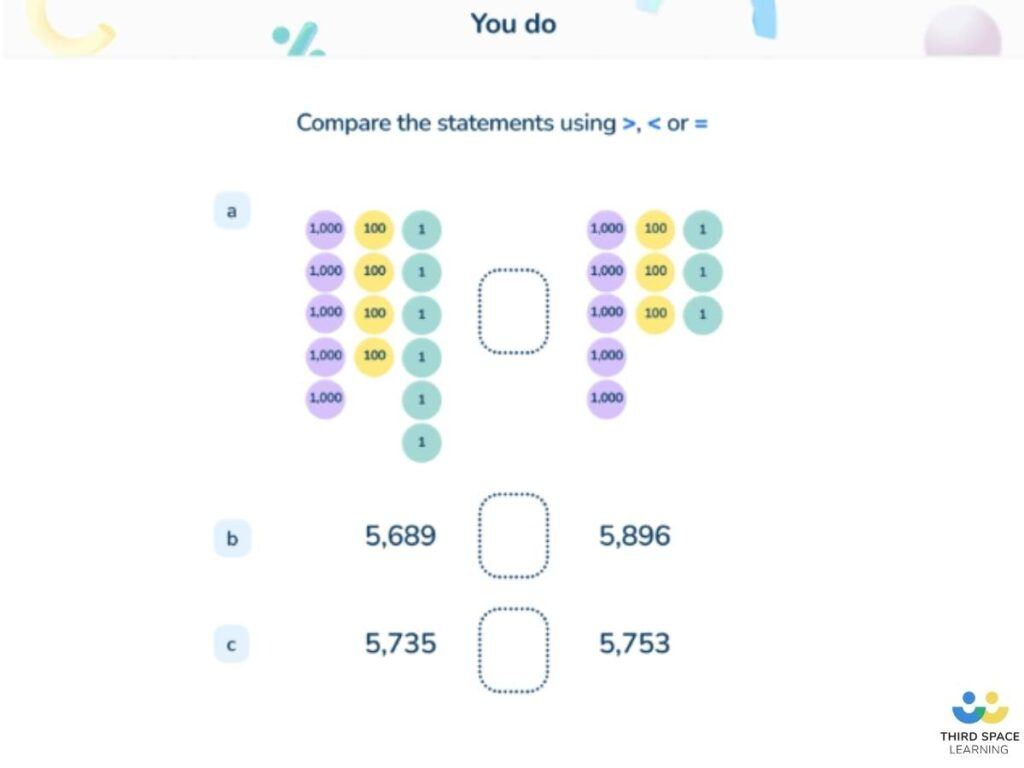
Read more: How To Use Maths Manipulatives In Class
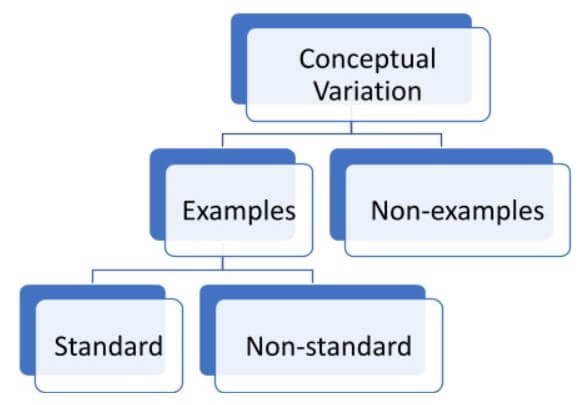
Standard and non-standard in Variation Theory
Once students have developed a sense of what the critical aspect is and is not, it is important to then demonstrate this aspect in both standard and non-standard forms.
I remember the first time that students I was teaching came across a calculation where the equals sign came before any digits and other symbols ‘__ = 8 + 9’. There were looks of bewilderment as if they had been tasked with the impossible. The fault of this confusion was entirely my own as every question I had ever asked focused on the standard form when writing calculation ‘8 + 9 =__’. This meant that students had not fully grasped the concept of the symbol and its critical feature; that it is there to represent equivalence, not just as a symbol that is used to write down an answer afterwards.
In my teaching sequence for teaching equivalence and the equals sign, after looking at examples and non-examples, I should have then looked at standard and non-standard forms like those below:
__ = 8 + 9
10 + 7 = 8 + 9
This graphic might be useful in highlighting how these components fit together.
Procedural variation: what’s the same, what’s different and what do you notice?
We can use procedural variation to highlight patterns within a set of questions that bring about a critical learning point or object of learning. Say we wanted to draw students’ attention to one of the field axioms of multiplication – distributivity – so that they can employ it at will when dealing with any multiplication. We may present this in the following way:

The incorrect way to go about this would be to treat this as a worksheet, in which you deliver an input and tell the students to crack on and complete it. There would be no method to that madness, and the opportunities for bringing out new and previous learnt relationships between the numbers would likely fall by the wayside for all students, or would only be found by those who are high attaining in mathematics.
Rather, a more controlled approach should be taken. You should ask students to complete the first two questions and then ask them, ‘what is the same, what is different and what do you notice?’ This will provide the opportunity to pick up on what the design of these minimally different questions is attempting to draw out.
Procedural variation steps
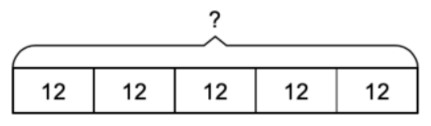
Firstly, you would want students to notice the relationship between the multiplicand from the given statement (12) and the combination of the multiplicands from the first two equations (11 + 1 and 10 + 2). Students will be drawn to the fact that they all total the same and that the product is also going to be 96.
From here, students can see if that holds true for the next two questions. The danger of letting students complete all 4 questions first without discussing it could result in students seeing that the product is the same, but not understanding the relationship between the multiplicands.
Notice that the 5th question in the sequence does not maintain the same pattern exactly. The multiplicands total 12, but the multiplier is now half of the original. This is to stop students aimlessly writing 96 down without giving any thought.
Crucially though, the statement at the beginning can still be used to solve this as the answer will be half of 96. This relationship between the multipliers can also be brought out. Question 6 allows the commutative law of multiplication to come through, as well as the associative law, and the final question reinforces division as the inverse of multiplication.
At all points of getting students to answer these questions in a controlled environment, the questions, ‘what is the same, what is different and what do you notice?’ are the ones used most, so that students can attend to those differences and similarities. Indeed, completing the above exercise could take up the vast majority of the lesson and students would get more from completing it than a whole worksheet.
Problem solving in procedural variation
At the heart of procedural variation are three forms of problem solving:
- Varying a problem – extending the original problem by varying the conditions, changing the results and generalisation;
- The use of multiple methods of solving a problem by varying the different processes of solving a problem and associating different methods of solving a problem;
- Multiple applications of a method by applying the same method to a group of similar problems.
1. Procedural variation: varying the problem
This form of variation aims to consolidate a concept by varying certain conditions to bring information, often information that is in conflict with students’ current understanding of the concept, to light. Look at the example below:

The variation within these problems should be self-evident. The amount of apple juice remains a constant, with only the amount that each jar holds getting varied question by question. Students are often comfortable with division as sharing into equal groups (especially at primary school), where students may generalise that dividing results in making something smaller.
It is this misconception that the example above attempts to exploit through the last three questions. Indeed, we see that dividing by a whole number and decimal produces a quotient greater than the dividend.
2. Procedural variation: varying the method
This type of variation is one that many teachers do, but may not be aware of. Simply teaching and demonstrating different methods in solving a problem is the first step in this type of variation, but its success lies in being able to draw out what students notice about the similarities and differences between each representation. Here are a few worked examples to vary the method for solving 12 × 5.
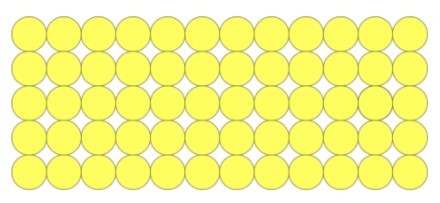
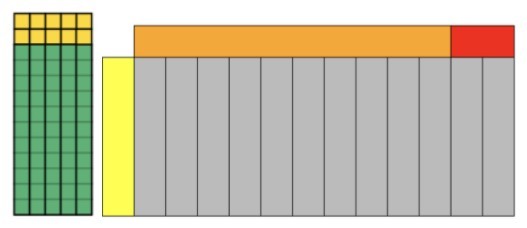
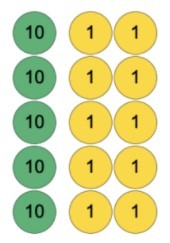
Your school’s calculation policy should set out what methods will be introduced and when. White Rose Maths have produced a calculation policy that looks at what different methods may be taught. That document is available from TES for free.
3. Procedural variation: multiple application of a method to similar problems
This final example looks at bringing about variation, not through changing the method, but with the application of a method or representation against a group of varied yet similar problems.
Variation Theory examples KS1
In KS1, this may look like the following:
1) James has 8 flowers and Julie has 5 flowers. How many flowers are there altogether?
2) James has 5 flowers and Julie has 8 flowers. How many flowers are there altogether?
3) There are 13 flowers, some are red and some are blue. 8 are red. How many are blue?
4) There are 13 flowers, some are red and some are blue. 8 are blue. How many are red?
Here the problems are varied, yet placed within a similar context, and the numbers used are the same, yet what each question is asking students to do differs slightly. For example, for question one, students may use Cuisenaire rods to visualise the problem. They would lay down the yellow rod and the brown rod to make a train and then the orange and the green above (or below) to help solve the total.
Question two enables students to experiment with the commutative law of addition. Notice how all the rods used are the same, but the order in which the bottom train has been constructed has changed. The underlying structure remains unchanged.
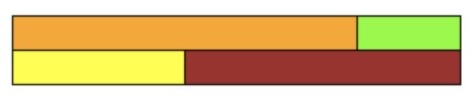
Question three tells us that there are thirteen flowers altogether and 8 of them are red. The next step would be to see how many more are needed to take 8 up to 13. Students may initially use white rods before exchanging it for a yellow rod of equal value. Again, the underlying structure of the problem remains unchanged.
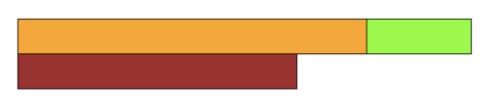
The final question is merely the inverse of question 3. We know the total amount of flowers and that a certain subset of them equal 5. Therefore, to find the missing amount, we need to count up from 5 until we get to 13. Again, students may need to use 8 white rods first, but they will see that this can be exchanged for a brown rod.
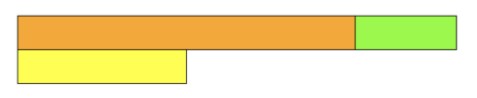
By the end of this exercise, students will be able to see that the 4 questions have similar underlying structures despite the variation within the problems.
Variation Theory worked examples
As mentioned above, just providing students with questions that contain aspects of Variation Theory will not bring along the benefits of the approach. Therefore, if you do not understand the variation taking place, it would probably be best not to use those examples.
For each of these, we need lots of examples of what the type of variation you’re referring to looks like ‘in practice’. In other words, with reference to regular sorts of questions and learning objectives from the national curriculum, so teachers can read it and see how they could try implementing it in their own lesson.
If you can pull from each of the main national curriculum topics that would be great, but it’s really just a case of showing the wide variety of ways people can think about including this practice in their teaching.
Number examples: number and place value
The examples below vary the representations to give access to the same idea. This approach can be easily transferred across all year groups to look at place value objectives. Using this in a KS1 class would involve looking at each representation and guiding the students through the process of asking ‘what is the same, what is different, and what do you notice?’ Introducing students to these questions early on will hopefully result in them becoming internalised automatically and so students will come to naturally ask themselves these questions.
The use of colour is particularly useful here as it supports connections between the place value counters, cards and base 10, but the presence of the Cuisenaire rod and the Numicon (whose colours do not conform to this) stops the association of ‘tens’ being green etc.
A crucial element to draw out of students is the unitization of 2 in some representations or where the 2 has been conserved as 2 ones. The number grid provides an opportunity to link these representations within the abstract number system.
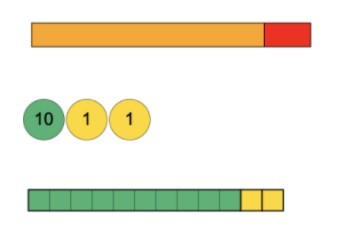
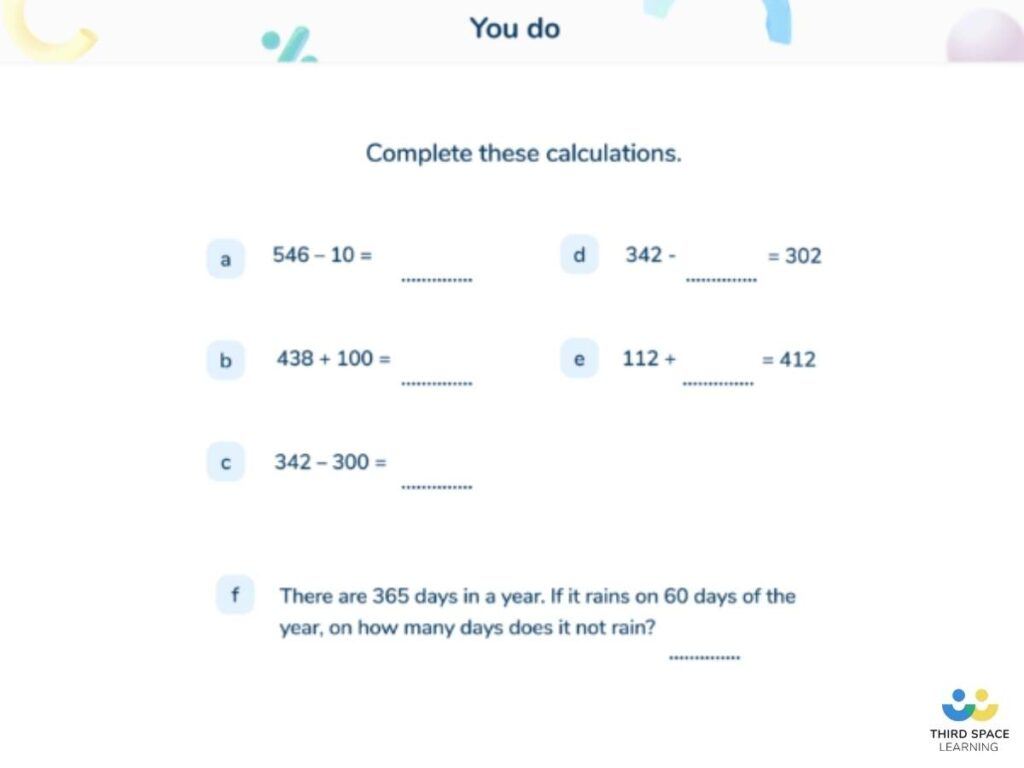
Number examples: addition and subtraction
563 – 100 = ___ – 200
387 – 100 = ___ – 200
983 – 100 = ___ – 200
___ – 100 = 874 – 200
This question focuses on subtracting by multiples of 100 and students’ understanding of the equals sign. It is the subtrahend that remains invariant while the minuend varies. This is done so that generalisations can be brought about in regard to the subtraction of multiples of 100. The minuends themselves play no major role in bringing about the effects of Variation Theory.
Here, we would want students to understand that ‘equals’ does not mean ‘answer’, but rather that two mathematical statements are balanced and produce a product that is the same as each other.
We can also bring about the relationship between the two minuends, one of which is unknown, when compared to the effect of subtracting the first one by one hundred. Namely, that the tens and ones do not change and that as the subtrahend has increased by 100 from 100 to 200. In order for the proportionality to remain constant between each statement, the minuend must also increase by 100.
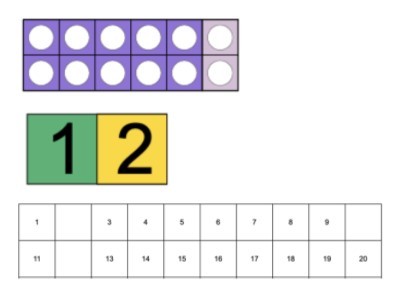
It would be in the interest of students to quickly subtract a multiple of 100 from a 4-digit number where the difference is a 3-digit number in subsequent lessons so then they can see the impact this can have on the generalisations they are producing.
Number examples: multiplication and division
What is the same/different and what do you notice?
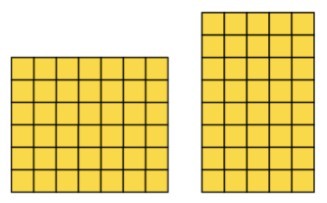
__ × 5 =__
5 × __ =__
__ =__ × __
__ + __ + __ + __ + __ = __
__ × 7 =__
7 × __ = __
__ =__ × __
__ + __ + __ + __ + __ + __ + __ = __
Write what you notice below.
This task links multiplication to the array/area model of multiplication, the understanding of the equals sign, the commutative law of multiplication and multiplication as repeated addition.
Pupils will recognise that the answer is 35 and that in the first model they can see 7 groups of 5 when looking vertically across from left to right. When looking at it horizontally from top to bottom, 5 groups of 7 can be seen. They can use these facts to write a multiplication calculation where the product is written first to bring about their understanding of the equals sign, and relate the multiplication of each vertical column to repeated addition of the number of columns in total.
The opposite is the case with the second representation where there are 5 groups of 7 on the horizontal and 7 groups of 5. Such activities will aid in pupils’ understanding of the difference in visual representation when the same numbers are used as multiplicand and multiplier across two different calculations.
Number examples: fractions, ratio and proportion
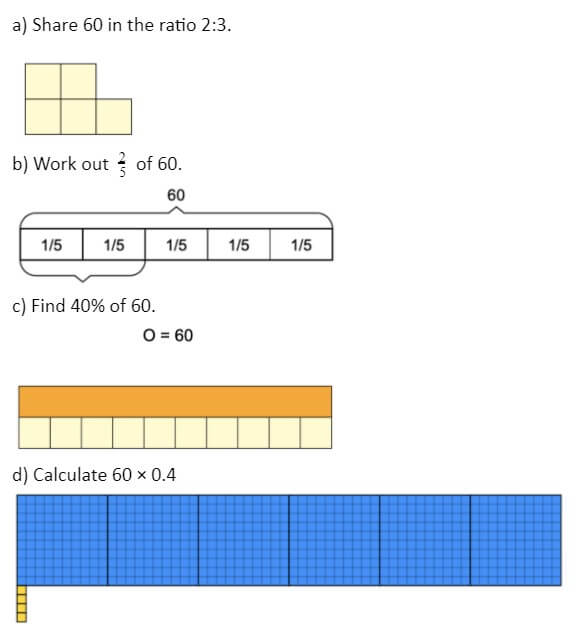
This series of questions is designed to link all the above areas of fraction as well as ratio. This is important as the connections between percentages and ratio can be missed and so more time than needed is used to teach the concept of ratio.
Here the methods used vary but the question is exactly the same, albeit in the context of the concept that it is drawing out. As such, the answer will be exactly the same for each question (24), but the methods and mathematical thinking behind each approach will draw out the connection between the question, as well as the different representations that have been used, such as the numerator and denominator of a fraction. Notice how all of the above are either concrete or pictorial.
Measurement examples
The following task comes from @J0shMartin and his contribution to Craig Barton’s Variation Theory website. Although this is predominantly a secondary-based website, there are some examples that are relevant to KS2. The following task requires students to notice patterns when converting between measurements (something students should have some understanding of doing BEFORE they embark on this task).

The answers are provided below:
- 3 m
- 0.3 m
- 0.3 m
- 0.03 m
- 4500 mm
- 450 cm
- 45 cm
- 5 cm
- 50 mm
- 15000 m
- 1500 m
- 100 m
- 50 m
As this is a context that many teachers are familiar with, here it would be best for you to try and consider how the questions have been carefully crafted to bring about variation, and how you might go about using this sequence within your own lesson. Consider the questions you would ask, the number of questions you would get the students to answer before stopping them to discuss the task so far, and how you would explain the patterns to the students.
Geometry examples: properties of shapes
Property of shape is a particularly useful curriculum area to deploy Variation Theory and can be used from year 1 onwards to great effect. Below is a sequence of slides used in a lesson on describing rectangles with some year 1 students.
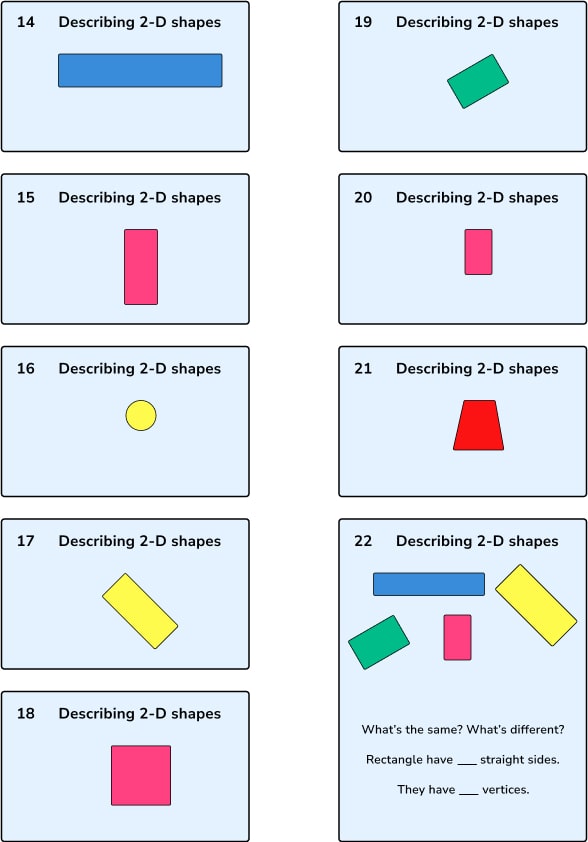
The rotation, colour and the type of shape have all varied so that students can generalise about the properties of rectangles (many believed that the ones on slide 17 and 19 were not), so they can really see the distinguishing features of the shape and not get caught on elements that are not important.
This is the conceptual variation as outlined at the start of this blog in action. It uses examples and non-examples, standard and non-standard examples to draw out what it means for a shape to be a rectangle.

Variation Theory FAQs
A learning method which shows various examples of the same concept, making it easier to decipher what are constant properties within that concept, and what differs between examples.
Variation theory is certainly used when teaching primary maths and is especially useful when teaching visual concepts such as properties of shapes. For example, pupils shown a triangle in different rotations can see that what makes them all triangles is their three sides. It is also a great way to instil mathematical methods, such as those used in algebra, by giving the same types of questions with different variables.
Variation theory can help develop pupils’ analytical and problem solving skills. Pupils can train their minds to look for particular properties as well as pull out anomalies. It is a great way to get pupils to really digest and think about the information they receive.
Showing examples which are different AND the same is extremely important. A great method to stick to is showing a standard example, a non-standard example and a non-example.
The two main types of variation theory are procedural variation and conceptual variation. As the names suggest, procedural variation changes the procedure in which things are carried out, whereas in conceptual variation the presentation of information is what changes.
Enjoyed this? Why not try our ‘How I Wish I’d Taught Maths’ series, inspired by Craig Barton’s bestselling book:
- Cognitive Load Theory in the classroom (1)
- Direct Instruction And Rosenshine Principles of Instruction (2)
- Goal Free Problems And Focused Thinking (3)
- Deliberate Practice In Education (4)
- Critical Thinking Skills And Problem Solving Activities KS2 (5)
- How Retrieval Practice Helps Long-Term Maths Skills (6)
- Plus: Most Effective Teaching Strategies
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.




