Applying Rosenshine’s Principles in Maths Lessons: A Practical Guide
Rosenshine’s principles of instruction combine three areas of research to address how people learn and retain new information. Barak Rosenshine’s principles combine cognitive science, classroom practices and cognitive support to offer educators guidance on effectively implementing instructional principles for their students.
This article provides practical advice to help teachers implement Rosenshine’s principles of instruction into any lesson. While many of the examples relate to mathematics lessons, the principles can be applied in similar ways across all subjects.
What are Rosenshine’s principles of instruction?
Rosenshine’s principles of instruction are a set of evidence-based recommendations for teachers looking to use educational psychology to improve their students’ learning.
Each principle can be applied to any subject and will benefit learners at every stage of their school career.
Evidence supporting Rosenshine’s principles of instruction
Rosenshine combined cognitive science, educational research and observations of the most effective teachers to determine which instructional procedures would have the greatest impact on students’ attainment.
Educational research often feels too inaccessible or difficult to verify, which is why the triangulation employed by Rosenshine is so reassuring to teachers.
Barak Rosenshine’s findings made research-based strategies more accessible to teachers, meaning they no longer need to rely on anecdotal evidence and personal experience to determine classroom practice.
Many of the principles are supported by cognitive load theory and the limited capacity of our working memory. For example, providing scaffolding for difficult tasks and presenting new information in small steps reduces cognitive overload and supports the transfer of information into our long-term memory.
Maths Leader’s Toolkit
Adaptable tools, templates and action plans to guide you step by step to create a maths scheme of work to maximise learning.
Download Free Now!Rosenshine’s original 17 principles of instruction
Originally, 17 principles of instruction emerged from Roshenhine’s research:
- Begin a lesson with a short review of previous learning
- Present new information in small steps with student practice after each step
- Limit the amount of material students receive at one time
- Give clear and detailed instructions and explanations
- Ask a large number of questions and check for understanding
- Provide a high level of active practice for all students
- Guide students as they begin to practise
- Think aloud and model steps
- Provide models of worked-out problems
- Ask students to explain what they have learned
- Check the responses of all students
- Provide systematic feedback and corrections
- Use more time to provide explanations
- Provide many examples
- Reteach material when necessary
- Prepare students for independent practice
- Monitor students when they begin independent practice
(Rosenshine, 2012)
In 2012, Barak Rosenshine detailed 10 of his principles of instruction in an American Educator article. Tom Sherrington organised these principles into the following four categories in 2020:
Sequence concepts and modelling
- Present new material using small steps
- Provide models and examples
- Provide scaffolds for difficult tasks
Questioning
- Ask questions
- Check for student understanding
Reviewing material
- Daily review
- Weekly and monthly review
Stages of practice
- Guide student practice
- Obtain a high success rate
- Independent practice
This article focuses on how teachers can put these 10 principles into practice in the classroom and how to use Tom Sherrington’s four categories to add the principles into lesson planning.
Rosenshine’s 10 principles in action
Here, in detail, are the ten principles of instruction that Rosenshine and Sherrington have identified as having the greatest impact on teaching and learning. Research supporting each principle is provided along with examples showing how it can be put into action in the classroom.
While the principles can be applied to different school settings and subjects; finding the most appropriate way to apply each principle to a teacher’s individual context is a valuable form of continual professional development (CPD).
1. Daily review
The first principle recommends students should review prior learning every day. Recalling information from their long-term memory strengthens retention of the information students are being asked to recall and retention of related information.
Every time a student activates a schema of prior knowledge it becomes easier for them to access it in the future. This means they can go longer between subsequent recalls without loss of accuracy.
In addition to strengthening the pathways that lead to prior learning, daily recall helps student reorganise their long-term memory and incorporate new knowledge into pre-existing schemas. Teachers can encourage students to do this by activating the most relevant prior knowledge at the start of a lesson.
Common approaches to daily recall include:
- Low-stakes quizzes
- ‘Information dumps’
- Diagnostic questions
- Key terms tests
- Mental arithmetic questions
- Past paper questions
Refreshing relevant skills at the start of a lesson reduces students’ cognitive load, making it easier for new learning to occur.
To prepare students for a lesson on the area of rectangles, the teacher may begin with a times tables test because multiplying two numbers together is a prerequisite for finding areas.
Ahead of a lesson on adding fractions, students could be asked to find the lowest common multiple of different pairs of numbers.
Daily review should not be limited to information related to new content covered during a lesson. Prior learning should be constantly reviewed, with the intervals of spaced retrieval becoming increasingly longer.
A low-stakes quiz covering five to eight different topics at the start of every lesson will allow the whole syllabus to be reviewed multiple times throughout the year.
Although daily review takes lesson time away from learning new content, it saves time in the long run because previous learning is retained and does not need to be retaught.
Simple ways to incorporate daily review into a mathematics lesson:
- Questions on mini-whiteboards at the start of a lesson
- Exit tickets handed in at the end of a lesson
- Mental arithmetic test
- A low-stakes quiz
- Including questions from previous topics in homework task
- Interleaving an old topic with a new one (e.g. calculating averages from a set of answers)
Each Third Space Leaning online one-to-one maths tutoring session begins with a review of prior learning. Students answer two questions based on the lesson objective to make connections between prior learning and the lesson’s objectives. If students answer correctly, they proceed with the learning objective. If they answer incorrectly, tutors recap the prior learning students need to access the lesson content.
2. Provide new material in small steps
Successful teachers are likely to provide students with new information in small steps. Use of direct instruction allows the teacher to control students’ exposure to new information in a controlled and gradual way.
This approach is so effective as it minimises the demand on students’ working memory. Cognitive load theory states that this enables students to process the new information more effectively, and accurately encode it into their long-term memory.
Development of subject-specific pedagogy allows teachers to use sequencing concepts to gradually build up students’ mastery of prerequisite skills before attempting new topics.
Schemes of work and spiral curriculums are often designed with this in mind; for example, teaching the area of rectangles before finding the surface area of a cuboid.
Complex tasks, such as finding the equation of a straight line, can be broken down into its key components and practised separately before being brought together in a single question. For example:
- Find the gradient of a line segment
- Write down pairs of coordinates
- Substitute into a function to find a missing value
- Rearranging formulae
- Solving equations
Simplifying how new information is presented and reducing cognitive load means that students can learn more complex problem-solving skills. Students learn more when challenged, but this challenge should come from the content, not the way the new content is delivered.
Every Third Space Learning lesson follows an ‘I do, we do, you do’ approach. Maths specialist tutors break down new skills and concepts into small steps with visual representations and model how to solve them. Students then complete each small step together with their tutor and, when ready, independently.
3. Ask questions
Formative assessment such as asking students questions during lessons presents many benefits:
- Teachers can check students’ understanding
- Students actively engage with the material
- Responses can help teachers to identify misconceptions — effectively achieved by using diagnostic questions
A further benefit to asking questions during learning is that it helps students assimilate new material with prior learning:
- Have you seen this type of problem before?
- What method did you use the last time you answered a similar question?
Questioning also encourages elaboration, generates examples and non-examples, challenge students’ misconceptions and develops metacognition: students’ ability to plan, monitor and evaluate their own learning.
Metacognitive prompts provided by teachers, such as ‘Does your answer make sense?’ will eventually become internalised by learners and they will start to spontaneously ask themselves the same questions.
One of the greatest challenges teachers face when asking questions is ensuring that all students get the opportunity to answer them. Giving students time to process questions and then cold calling is a common approach to encouraging all students to engage with the question being asked.
Think, pair, share is also an effective method: students answer the question alone (think), tell their answer to a partner (pair), and the teacher calls upon someone in the room for an answer (share).
Effective questioning strategies in mathematics include:
- Low-stake quizzes
- Answering on mini-whiteboards
- Think pair share
- Diagnostic questioning
Resources: KS2 diagnostic questions
Third Space Learning’s academic team considers effective questioning opportunities when designing each one-to-one maths lesson. Every lesson is prepared with a set of notes for each highly trained tutor to use, complete with questions to ask students. Questions match each aspect of the lesson to check for student understanding.
4. Provide models and examples
Provide models for students as they build their competency in a new skill to reduce cognitive load. Models allow students to understand the success criteria of the new task and provide a framework.
Exam boards often provide exemplary answers for this purpose. Worked examples can also provide students with an excellent level of cognitive support when learning new skills. These approaches allow students to focus on understanding one element of the new skill at a time, which means that it can be encoded into their long-term memory before they try to acquire additional skills.
Worked examples are particularly effective in mathematics because students often need to learn complex and multi-step methods. Solving equations where the unknown is on both sides of the equals sign can be effectively taught through worked examples.
Students can first be presented with every line of the method complete except for the final step. In subsequent examples, additional lines of the method can be left out and students can use the previous examples as models to complete the method.
Worked example resources:
Every carefully designed one-to-one maths lesson from KS2 through to GCSE provides students with clear models to help them consolidate their understanding of complex mathematical concepts. Incorporating visual models, worked examples and sentence stems on learning slides reduces cognitive overload and allows students to focus on the skill and process.
5. Guide student practice
This principle of instruction relies on the excellent execution of the previous principles. Guided practice will only be effective if students have learned the new material successfully.
Once students have acquired a new skill through direct instruction, it is imperative they have opportunities to practise the new skill through repeated retrieval practice.
Purposely select questions of increasing difficulty for students to complete during guided practice to enable them to consolidate new information. This also increases the likelihood accurate recall it in the future.
Provide students with worked examples or opportunities to answer questions with their peers, these are two common forms of guided practice.
In mathematics, ‘I do, we do, you do’ is an effective form of guided practice. As students answer questions using their new skill with a gradual release of responsibility moving from the teacher to the student.
Differentiated worksheets, with increasingly challenging questions, provide an excellent opportunity for guided practice.
To be successful, all these examples must follow on from effective instruction.
Read more: How to teach primary maths
An ‘I do, we do, you do’ pedagogy allows tutors to model and guide student practice. Asking students to talk through the tutor’s example allows the tutor to ascertain whether the student has understood the process. Hearing the student talk through their practice helps the tutor identify any misconceptions and address them in real time, guiding the students learning.
6. Check for student understanding
The most effective teachers adapt their lessons based on student understanding. Formative assessment, or assessment for learning, must employ robust methods to check the understanding of all students throughout every lesson.
This principle is closely related to Rosenshine’s second principle — ask questions. Often, effective questioning is the most common way to assess students’ understanding.
Diagnostic questions are effective when checking students’ understanding because incorrect answers highlight specific misconceptions that can subsequently be addressed.
Students’ responses to the guided practice questions show whether they have understood the new content. But this is only possible with immediate and regular feedback.
Providing students with model answers and regular reminders to check their work reduces teacher workload without detrimental effects on learning.
Think, pair, share, cold calling and writing answers on mini-whiteboards are all formative assessment examples that will encourage all students to engage with the questions used to assess their understanding.
For this principle of instruction to be effective, teachers must adapt their teaching based on students’ responses.
Every Third Space Learning session begins with a check for understanding of previous knowledge. Whether students answer the prior learning questions correctly or not, determines the trajectory of the lesson and the skills covered.
Throughout the lesson, tutors encourage students to talk through their mathematical processes and ask them structured questions throughout the lesson to check they have understood the concept. After completing the ‘I do, we do, you do’ section of the lesson, students complete a ‘go further’ question using the same maths skills and concepts in a new context to check for understanding.
Students complete post-session questions after each session to highlight any remaining misconceptions and check they have understood the concepts and are ready to progress.
7. Achieve a high success rate
A common misconception is that the relationship between effective teaching and students’ high success rate is one directional. Rosenshine’s research revealed that a high success rate can increase the effectiveness of subsequent teaching.
The optimal success rate is approximately 80%. At this level, students are being challenged enough to improve learning but not so much that they are experiencing cognitive overload.
Success is motivating and can improve students’ self-efficacy, which makes them more likely to engage in the lesson. A high success rate also indicates that the material is being delivered in small enough chunks to allow mastery before moving on to new content.
Provide students with model answers and worked examples to promote a high success rate during the early stages of learning. As students become more proficient in the new methods, temporary support can gradually be removed so the success rate remains the same while the complexity of the task increases.
Differentiated worksheets with questions of increasing difficulty will also achieve the same effect.
Read more: Differentiation in the classroom
Before starting one of Third Space Learning’s tutoring programmes, all students complete a diagnostic assessment to identify the maths concepts each student needs pracitce with most. At the end of the programme, students complete an end-of-programme assessment to highlight the progress made and high success rate.
8. Provide scaffolds for difficult tasks
Rosenshine’s next principle proposes scaffolding to minimise students’ cognitive load when tackling difficult tasks. Scaffolding complex tasks is similar to providing students with worked examples; both are designed to minimise the amount of new information that students need to process at any given time.
Heavily scaffold tasks and slowly remove the level of support so students are gradually exposed to more complex tasks. This should only take place after they have mastered the previous skill.
Writing frames and sentence stems are a popular form of scaffolding in many subjects. In mathematics, providing model answers or sentence stems with some details omitted is a more effective way to employ scaffolding.
Read more: 13 Effective teaching strategies
Third Space Learning’s highly trained and qualified tutors provide scaffolds for difficult task where appropriate for students. Each session is designed with a support slide for tutors. Maths experts identify areas of the lesson students are likely to find tricky and break them down using modelled examples, sentence stems and scaffolded questions for the tutors to prompt students’ mathematical processes.
9. Independent practice
Once students have mastered a new set of skills and completed guided practice, they are ready to move on to Rosenshine’s ninth principle: independent practice.
Rosenshine believes this principle offers students the opportunity of overlearning. When students are exposed to repeated retrieval practice of a single skill, it becomes automatic and performing the skill places little or no demands on working memory.
During independent practice, students can use the metacognitive skills developed during guided practice: planning, monitoring, and evaluating.
Independent practice should consolidate learning. It takes a lot of time but should not be overly demanding on students’ working memory or cognitive load.
Homework is a good opportunity for independent practice because students should be ready to answer questions or demonstrate a new skill with very little input from their teachers.
Maths experts have designed each lesson with opportunities for independent practice. During the ‘you do’ section for each learning objective, tutors actively step back to allow students to complete the question independently. This also provides tutors with the opportunity to assess how well students have understood the objective and whether they can apply the learning in a new context.
10. Weekly and monthly reviews
Weekly and monthly reviews are the final stages of the learning process. Retrieving prior knowledge a week or month after initial learning helps to strengthen the pathways to the information in students’ long-term memory.
In the absence of retrieval, memories will decay, but the rate of forgetting decreases significantly following repeated retrieval attempts.
When a new skill is learned, teachers should aim to test it the following lesson, the following week and the following month. But retrieval practice should not stop there. Using spaced repetition, it should be revisited each month or every other month in a starter activity, interleaving with another topic (such as adding fractions when learning about surds), or in a homework task.
Weekly and monthly reviews can be incorporated into a five-minute starter at the beginning of each lesson. Starter activities that can double as effective weekly or monthly reviews include:
- Keyword tests
- Translation exercises
- Multiple-choice questions
- Short-answer questions
When deciding what to set as a homework activity, aim for 60% of the content to be based on topics taught more than one week ago.
Students complete their one-to-one online maths lessons with the same maths tutor each week. This affords tutors and students the opportunity to review the learning from the previous week. Tutors can see how much information the student has retained and can remind them of the previous learning or slides if necessary.
Four categories of Rosenshine’s principles of instruction
This article has examined ten of Rosenshine’s principles of instruction. As mentioned, these principles can be summarised using four strands, identified by Tom Sherrington. These four strands can help break down Rosenshine’s ten principles of instruction to make them easier to apply in the classroom:
Sequence concepts and modelling
Rosenshine recommends that new topics are broken down into smaller skills or components, which are taught separately and mastered before moving on to the next skill.
To minimise the cognitive load associated with difficult tasks, teachers should provide models, worked examples and scaffolding when students are first introduced to new concepts.
Solving simultaneous equations, for example, could be broken down into solving two-step equations, substitution, expanding brackets, and collecting like terms.
Questioning
Ask questions to encourage engagement during a lesson, facilitate elaboration, generate new knowledge, test prior knowledge, check understanding and provide feedback to teachers about whether their lesson plan needs to be adapted.
Questions can also be used to encourage metacognition: ask explicit questions to students related to planning, monitoring and evaluating learning.
Reviewing material
Once new knowledge has been acquired, retrieval practice is essential to combat the steep forgetting curve that affects information stored in the long-term memory. The rate of forgetting significantly reduces after each subsequent recall.
New information should be tested at the first opportunity, normally the next lesson, one week after learning, and then monthly. Reviews can happen through starter activities, interleaving with new topics, or in homework tasks.
Stages of practice
Students need plenty of practice to master new skills. Opportunities to practise need to be structured in a way that offers a high success rate at every stage, with a gradual release of responsibility moving from the teacher to the student.
Use model answers, scaffolding, and worked examples can support students to complete guided practice before they are ready to complete questions independently, which is when the new skills can become automated.
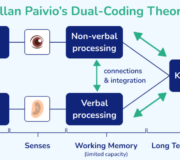
Read more: Dual Coding: A Teacher’s Guide To Increase Student Learning
Rosenshine’s Principles FAQ
Rosenshine’s principles of instruction are a set of recommendations to improve student learning. They emerged from the findings of cognitive science, educational research, and observations of teachers.
Sequence concepts and modelling, questioning, reviewing material, and stages of practice.
Scaffolding reduces the cognitive load of a task, which allows students to focus all of their attention on the main learning point. It is part of the modelling strand of Rosenshine’s principles and also features in guided practice.
Rosenshine’s principles of instruction have been shown to improve learning through educational research and are supported by cognitive science.
References
Rosenshine, B., 2012. Principles of instruction: Research-based strategies that all teachers should know. American educator, 36(1), p.12.
Sherrington, T., 2020. Rosenshine’s principles in action. Hachette UK.
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist school tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 169,000 primary and secondary students become more confident, able mathematicians.
Learn how tutors build rapport or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
