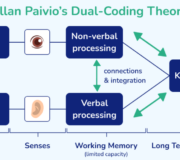
How to Teach Metacognitive Skills: Practical Examples For Primary & Secondary Students

Becoming a self-regulated learner involves more than simply studying hard. It requires a range of metacognitive skills that enable learners to create a plan, monitor their progress, and evaluate their performance against a learning objective. These abilities include self-awareness, cognitive strategies, and study skills. 

In this article, we’ll delve into the significance of metacognition in assisting pupils in becoming self-regulated learners. We’ll also provide the teaching model recommended by the EEF to teach metacognitive skills, with real examples from our maths intervention.

What are metacognitive skills?

Metacognitive skills are the ability to think about our own thinking and the processes we use to learn. These thinking processes enable students to set goals, select strategies to enhance their learning experiences, and use self-assessment or self-questioning to monitor their own learning. 

Metacognitive processes have become increasingly researched in recent years, with findings being applied to students’ problem-solving skills, study strategies, reading comprehension interventions, and learning strategies. 

When students use metacognitive activities effectively, they:

• set goals;
• select specific strategies to enhance their learning experiences;
• use self-assessment or self-questioning to monitor their own learning. 

Cognitive processes are the range of learning skills that students possess. In contrast, metacognitive processes enable students to self-evaluate the effectiveness of their cognitive processes (Schraw, 1998).

Metacognitive skills can become automatic, especially for teachers, which can make them difficult to identify, verbalise and teach. However, they can have a transformative effect on learners’ achievement, promote higher-order thinking skills and encourage a growth mindset. 

Research has shown that metacognitive abilities can be successfully developed by employing explicit teaching strategies in primary and secondary schools with many studies conducted in mathematics classrooms.

Examples of metacognitive skills

Here are a few metacognitive skills examples that can enhance student learning:

Planning Stage

The planning stage involves deciding whether to draw a sample space, Venn diagram or tree diagram when presented with a probability question.

When preparing for an assessment, it will also include students choosing between reviewing notes or answering practice-questions.  

At the planning stage of answering a problem, students may ask themselves the following type of questions:

• Have I done something like this before? If so, what did I do?
• How is this similar or different from the examples I’ve seen before?
• What can I find out, even if it isn’t what the question is asking for? 

Monitoring Stage

In the monitoring stage, students may regularly check their answers while completing an exercise to see whether they are using an effective strategy.

When solving questions involving angles, students may check whether their answers make sense compared to the diagram, for example, asking themselves if an acute angle makes sense in that particular situation.

Students may ask themselves the following type of questions:

• Am I getting the right answers?
• Am I using the most efficient method?
• Could I get the same answer using a different strategy?

Evaluating Stage

In this stage, pupils will consider the effectiveness of the specific strategies they selected in terms of accuracy and efficiency. 

For example, they may realise that using the alternate segment theorem would have been a quicker approach than using geometrical reasoning and other circle theorems to reach the correct answer.

When evaluating their performance, students may use self-reflection questions such as:

• Were any of my steps irrelevant?
• What could I do differently to be more efficient next time?
• Which topics should I revise before the next assessment?

Why are metacognitive skills important?

Research has shown that as students develop their metacognition in the classroom, their learning strategies become significantly more effective, resulting in an increase in pupils’ overall performance.

The impact has been calculated using different measurements, with results including:

• Metacognition accounts for 17% of a student’s success while at school.
• Metacognitive knowledge has an effect size of 0.53 on attainment.
• Effective use of metacognitive strategies is equivalent to an additional 7 months of secondary education.

Metacognitive strategies play a crucial role in education because they have a significant impact on attainment and can be effectively taught in school settings, as demonstrated by Perry et al. (2019). 

Metacognition in mathematics

Although the skills of planning, monitoring, and evaluating are common to all subjects, the way in which these skills are applied can vary depending on the specific subject. 

For instance, planning an essay requires a different skill set than planning how to find the tangent to a curve.

To foster metacognitive awareness in mathematics, learners must acquire it in the mathematics classroom. 

Research has shown that intervention programmes targeting metacognition improvement have been more successful at improving maths attainment in high schools and secondary schools compared to curriculum reform and computer-assisted instruction. Improving students’ metacognitive knowledge has also been shown to reduce maths anxiety, which can be a significant barrier to attainment for some pupils.

How to teach metacognitive skills

While the potential impact of developing pupils’ metacognitive skills is very high, little or no time is dedicated to teaching these skills in the curriculum. 

Teachers face the challenge of not having clear guidance about how to teach students metacognitive skills. Furthermore, any guidance offered must be interpreted in a context-specific way. 

Research has shown that students’ use of metacognitive strategies significantly improves when their teachers explicitly state the cognitive processes required to complete a task. The EEF recommendations feature many explicit instruction techniques for this reason.

The EEF has produced an evidence-based 7-step framework for teaching metacognitive skills that can be applied to all subjects. 

The following summary examines each of the seven stages and considers practical ways that these can be achieved in a mathematics classroom. 

1. Activating prior knowledge

When delivering a new topic, teachers should find opportunities to activate prior knowledge that is relevant to the new topic at the start of the lesson. 

This technique supports pupils to assimilate the new information with previously learnt material and also reduces the demands placed on their working memory during the lesson. 

Using a low-stakes quiz is one of the most effective ways of activating prior knowledge and can take as little as 5 minutes at the start of a lesson.

This could be a quick recap quiz as a class or could take the form of homework set in advance of a new lesson.

In this stage, the teacher directs the activity and identifies the relevant prior knowledge that needs to be activated. The role of the pupil is to retrieve the information required to complete the learning task.

Practical examples to activate prior knowledge

In Third Space Learning’s online one to one maths tuition, our lessons begin with an introduction slide to activate prior knowledge. Additionally, the tutor can use it diagnostically to get an understanding of what the student knows or does not know.

By asking carefully considered questions, tutors can model various planning techniques for their students

For the KS2 lesson, examples include:
• “What do you think the first step is when looking at the picture of the cubes?”
• “What ‘fraction words’ do you think you would need to be using to describe what you see?”

For the GCSE lesson, examples may include:
• “How do you know that Lee is correct?”
• “How has Jo/Lee worked out their answer?”
• “Do you remember the formula given by Pythagoras’ Theorem?”
• “How could you use it to answer this question?”
• “Would you change your method if you were not trying to find the longest side?”
• “How do you know which side is the longest?”

The tutor may also encourage monitoring metacognitive strategies. For example, asking students:
• “How confident are you about your explanation?”

2. Explicit strategy instruction

Explicit instruction is an important stage in developing metacognitive skills. 

It ensures that pupils are secure in their knowledge of the different cognitive strategies available to them for problem-solving. Explicit instruction is teacher-led and the quality of the instruction is likely to depend on the pedagogical knowledge of the teacher.

Providing clear worked solutions with notes that detail each step is an effective method for explicitly teaching new topics.

Practical ideas for explicit instruction of metacognitive skills

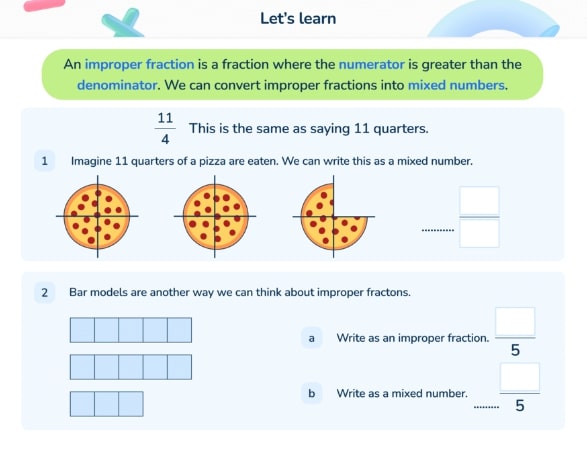
In our KS3 lesson, the explicit instruction stage teaches students how to use visual representations and bar models to help them understand conceptually how to convert between mixed and improper fractions.

Students could also be asked to evaluate the success of various cognitive strategies so that they are actively engaged in this stage. For example:
• How could you check if the mixed number you found is actually correct?
• How do you think a student may get stuck here?

Our GCSE revision programme takes a slightly different approach. As this is a revision programme, we want to ensure that revision is focused on the areas where pupils need the most support and doesn’t waste time on topics pupils are already secure in. For this reason, students jump straight into an exam style question without help from the tutor. The tutor can then use this as an assessment point and decide what level of instruction, modelling and guidance a student needs.

Does the pupil already know which strategies to use and accurately carry them out? If yes, pupils can move onto more independent practice. If not, tutors can explicitly teach pupils the strategies needed with the support slide.

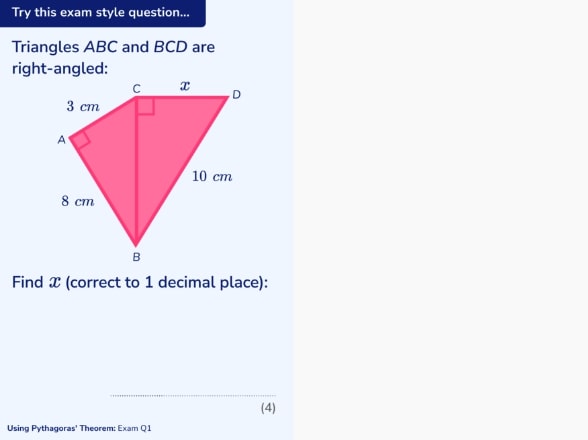
For example in this support slide, the student is guided through how to apply the formula for Pythagoras’ theorem to find both the hypotenuse and a short slide.

After explaining the formula, tutors may ask students to consider questions such as:
• How can I identify the hypotenuse (longest side) of a right angled triangle?
• If I knew the two shorter sides of a right angled triangle, how could I use Pythagoras’ theorem to find the hypotenuse (longest side)?
• If I had the hypotenuse and a shorter side, how could I find the other short side using Pythagoras’ theorem?

If needed, tutors may also choose to bring up a blank slide and draw out some simpler examples to build understanding.

3. Modelling of learned strategy

This stage is also teacher-led but the pupils will need to engage at a higher-level compared to the previous stage. 

Modelling a new strategy offers two important benefits for pupils. Firstly, they learn how to apply the new strategy to solve problems. Secondly, it is an opportunity for the teacher to model metacognitive strategies if they think-aloud and verbalise their decision-making processes.

Modelling a strategy using worked solutions has been shown to be an effective form of explicit instruction in mathematics, especially for novice learners (Manson and Ayres, 2019). 

However, expert learners benefit more from partial worked solutions due to the expertise-reversal effect. The amount of detail included in demonstrating a new technique should depend on the students’ proficiency and the difficulty of the technique.

Example-Problem Pairs is a very effective approach for modelling in mathematics. 

The teacher presents two very similar problems to the class (one on each side of the board). On one side, the teacher models a complete solution and students then attempt the question on the other side of the board, using the worked solution as a guide. 

Practical ideas for modelling of learned strategy

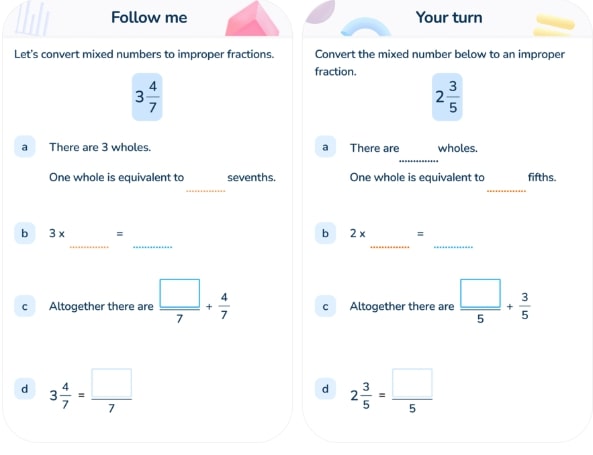
In our online one-to-one tuition, our tutors demonstrate maths concepts to students and also explicitly explain and demonstrate the metacognitive skills that students need to improve their maths performance.

Pupils and tutors can discuss ideas through their audio connection and the tutor can reveal the planning, monitoring and evaluating thought processes of an expert. 

For example:
• “The first thing I would always try to do with questions like this is to…”
• “I might check at this point that I am on the right track by…”
• “To check if the answer is correct, I would…”

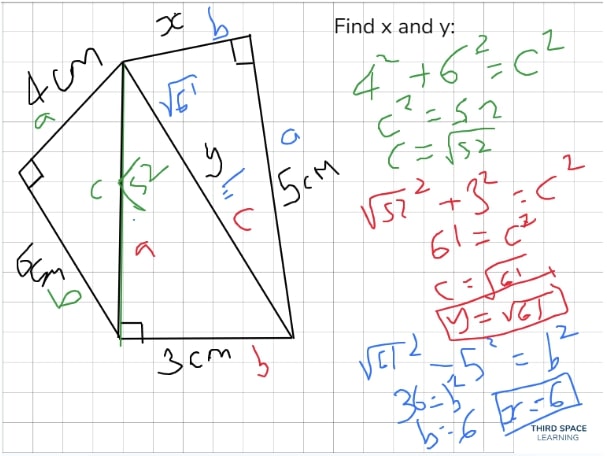
In our GCSE revision lessons, the support slide allows tutors to break down more complex questions and walk through them step by step.

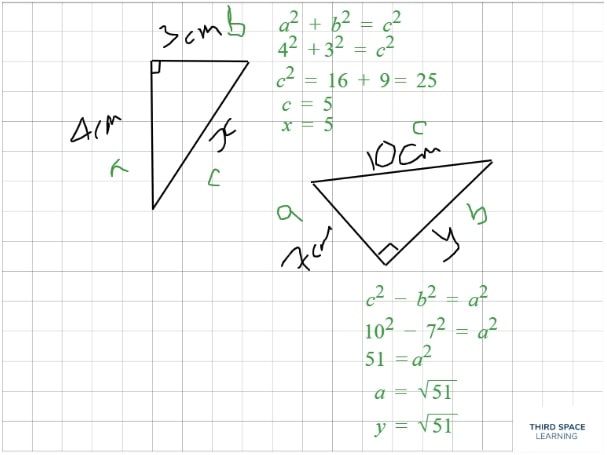
For example in this Pythagoras’ theorem question, a tutor would either model or guide the student through a problem solving approach by finding CB in order to find CD (x).
• “I have been asked to find x in this question, but I cannot find it straight away because I do not have enough information – what side can I find and how?”
• “How does finding CB help me to find x(CD)?”

4. Memorisation of learned strategy

Students will eventually need to memorise new strategies if they are to use them successfully under exam conditions. However, a teacher may choose to let their pupils refer to their notes in the early stages of the learning process. 

This benefits the pupils by reducing their cognitive load, allowing them to focus more on applying the new process rather than remembering it. 

Memorising a new strategy requires students taking responsibility for their own learning, with the teacher taking a supportive role.

Practical ideas for the memorisation of learned strategy

Within our intervention, we can encourage the memorisation of metacognitive strategies by prompting them as pupils attempt independent practice sections of the lesson.

The tutor can ask questions to make sure the pupil is practising using the metacognitive strategies the tutor just demonstrated. 

For example:
• What did you notice first?
• How could you check that the answer is correct?
• How do you know what strategies to use here?
• What could you start by working out?

5. Guided practice

Scaffolding is an effective form of guided practice: the process of supporting students to answer a question through a series of hints or prompts. 

In mathematics, scaffolding has been found to be positively correlated with the development of metacognitive strategies. 

Guided practice is likely to involve adapted activities, allowing pupils to work at different levels or at a different pace to each other.

Verification feedback (identifying if an answer is right or wrong without further explanation) is an effective way to support guided practice (Guo and Wei, 2019). Teachers act as facilitators at this stage with the majority of the work being completed by the students.

In mathematics, when students are given a copy of the answers, they can provide themselves with verification feedback which is an effective way to prepare them for independent practice.

In our intervention, paired examples give the student an opportunity to practise completing a question with a perfect model answer (as well as all the support they might need from their tutor). This provides scaffolding for the student to approach the question in easy digestible steps.

Practical ideas for guided practice

At Third Space Learning, our GCSE lessons provide as much or as little scaffolding as an individual student may need.

In our GCSE revision programme, once a student has completed a support slide, the tutor will ask the student to recall what they have learnt and then give them a chance to apply it once again. If the student seems confident, the tutor can take the student straight through to an assessment slide. If not, the tutor can pull up a blank slide and give the student more practice questions on the topic before moving on.

They might ask:
• Which side can we start by finding here ?
• How will you apply Pythagoras to answer this question?

The five preceding stages are essential stepping stones towards pupils being able to complete independent learning and practice. 

Independent practice involves intelligent practice where students get a chance to make active choices in how to manage, organise, deploy, monitor and evaluate metacognitive skills.

This stage is student-led and teachers are used as a source of expertise when necessary. 

For example, when pupils have an incorrect answer, they benefit most from being presented with the full worked solution and using this to identify their own mistake. Mathematics students found this approach to be more successful than having their mistakes corrected for them when learning to solve linear equations (Bringula et al., 2017). Exam boards have started to provide worked solutions and student-friendly mark schemes to support independent practice.

Practical ideas for independent practice

In Third Space Learning’s tuition, pupils have a tutor on hand to give effective and timely feedback whilst supporting motivation with specific praise that develops a growth mindset. 

For example:

• “Excellent demonstration of converting to an improper fraction correctly, I saw that you drew a bar model and that helped you remember what to do!”
• “I see you picked up on the mistake in the last question correctly, can you explain why so many pupils make this mistake?”

At GCSE, our exam question slides give students the ability to demonstrate and practise what they have learnt. Tutors encourage students to talk through their thought processes as they choose which strategies to use in order to break down each question:

• Can you approach this question by yourself?
• What strategies are you going to use?
• Can you talk me through your thinking?

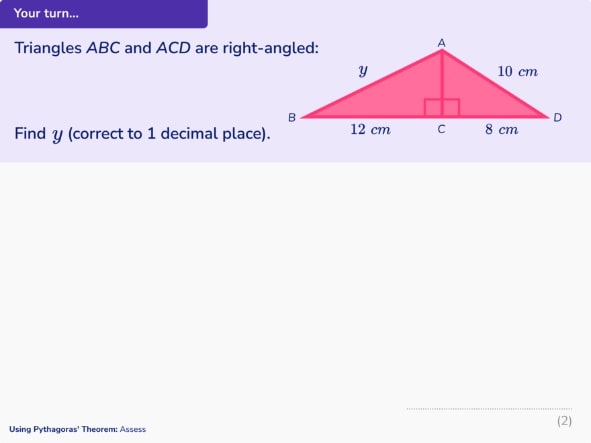
During independent practice, challenge is also crucial to allow students to develop and progress their knowledge of tasks and themselves. Our Third Space Learning lessons end with a challenge slide which extends pupils’ thinking.

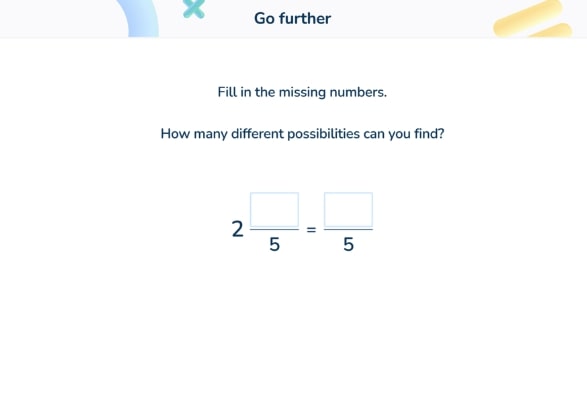
Extension questions in our GCSE programme allow for all pupils to be stretched and supported in the way that best supports their learning. These also give them an opportunity to think about how they can apply the strategies they have practised in a more unexpected context. For example, in the challenge question below, students need to either mentally construct or sketch the triangle described in order to apply the techniques they have learnt in the lesson.

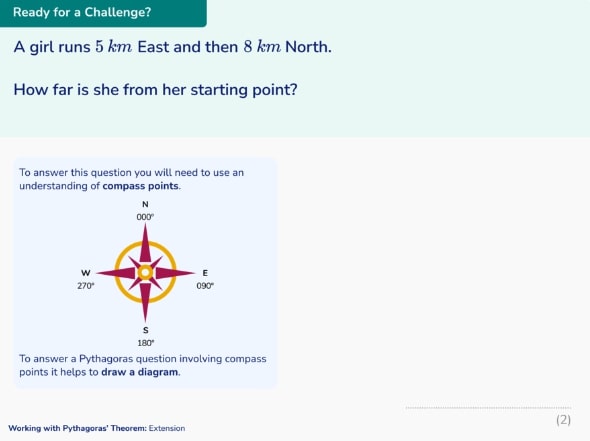
7. Structured reflection

When students are encouraged to share reflections of the learning process with their teachers, it significantly improves pupils’ ability to use metacognitive strategies. 

Part of its success is because it provides opportunities for teachers to intervene or adapt their strategies to further enhance students’ learning. 

For example, secondary students’ attainment when learning Pythagoras’ Theorem was significantly higher when metacognitive prompts were introduced at the end of each lesson compared to control groups taught by the same teacher (Baliram & Ellis, 2019). 

The prompts completed by the students were:

• ‘Today, I learned…’
• ‘I can now apply…to solve…’
• ‘I understand…but still don’t understand…’

The first 5-10 minutes of the next lesson was dedicated to whole-class feedback based on any misconceptions identified by the teacher from these prompts. 

A test at the end of the 4-week learning period and a retention test after a further 4 weeks showed significant gains over the control group who used the first 5-10 minutes of each lesson to consolidate the material learnt in the previous lesson.

Practical ideas for structured reflection

This is why we build in structured reflection time into our Third Space Learning lessons.

Structured reflection time is when a tutor questions pupils to encourage active reflection on their learning.

Tutors are trained and empowered to select the most appropriate level of reflection for the pupil from a range of questions (above) structured using Bloom’s taxonomy. 

At the end of GCSE lessons, pupils are presented with two questions that have been answered incorrectly. Students will need to reflect on their learning and explain their ideas. This allows students to both review their learning and also consider the possible misconceptions that could be made. 

This reflection time further supports the memorisation of the learned strategy and students recall their learning and verbalise it to their tutor.

References

Baliram, N. & Ellis, A. (2019). The impact of metacognitive practice and teacher feedback on academic achievement in mathematics. School Science and Mathematics, 119(2), 94-104.

Bringula, R., De Leon, J., Rayala, K., Pascual, A. & Sendino, K. (2017). Effects of different types of feedback of a mobile-assisted learning application and motivation towards mathematics learning on students’ mathematics performance. International Journal of Web Information Systems, 13(3), 241-259.

Cromley, J.G. and Kunze, A.J., 2020. Metacognition in education: Translational research. Translational Issues in Psychological Science, 6(1), p.15.

Guo, W. & Wei, J. (2019). Teacher Feedback and Students’ Self-regulated Learning in Mathematics: A Study of Chinese Secondary Students. The Asia-Pacific Education Researcher, 28(3), 265-275.

Manson, E. & Ayres, P. (2019). Investigating how errors should be flagged and worked examples structured when providing feedback to novice learners of mathematics. Educational Psychology.  DOI: 10.1080/01443410.2019.1650895.

Perry, J., Lundie, D. and Golder, G., 2019. Metacognition in schools: what does the literature suggest about the effectiveness of teaching metacognition in schools?. Educational Review, 71(4), pp.483-500.

Flavell, J.H., 1979. Metacognition and cognitive monitoring: A new area of cognitive–developmental inquiry. American psychologist, 34(10), p.906.