One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Arithmetic Quadratic sequences Fractions of amounts Square numbers and square roots Triangles Substitution Quadratic equation Sequences Nth termThis topic is relevant for:

Triangular Numbers
Here we will learn about triangular numbers, including how to find the next triangular number in a sequence (including picture sequences). We will also learn how to find triangular numbers and determine whether a number is a triangular number using the nth term.
There are also triangular numbers worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are triangular numbers?
Triangular numbers are numbers that can be represented as a triangle. The numbers form a sequence known as the triangular numbers.
The first triangular number T_{1}=1 .
The second triangular number is found by adding 2 to the previous one.
So, T_{2}=1+2=3.
The third triangular number is found by adding 3 to the previous one.
So, T_{3}=3+3=6.
Continuing this pattern, you get,
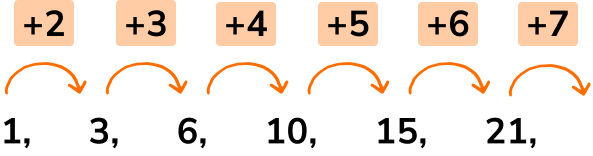
This produces the sequence of triangular numbers,
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, ...To determine the next triangular number in a numerical sequence, when given the sequence, we need to find the difference between the previous two terms and add one more than this value.
Visual representation
Triangular numbers can be represented using equilateral triangles. The number of dots within each triangle determines the value of the term. Each new row of dots in the triangle contains one more dot than the row above, creating a triangular pattern.
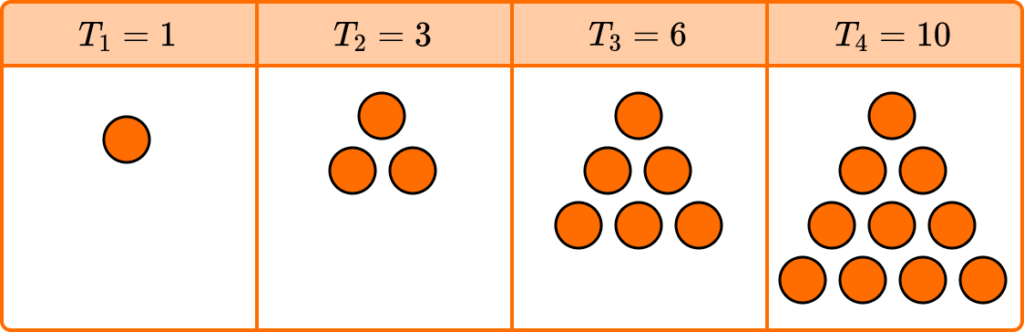
Triangular numbers are natural numbers. Carl Gauss and Pierre de Fermat are known for their work with number theory.
Triangular numbers were originally explored by the Pythagoreans who developed many relationships between different geometric shapes and numbers including triangular numbers, square numbers, pentagonal numbers (numbers represented within a regular pentagon) and hexagonal numbers (numbers represented within a regular hexagon).
These are sometimes known as polygonal numbers or figurate numbers.
To determine the next triangular number in a pictorial sequence, we add another row to the triangle that contains one more element than the previous row.
What are triangular numbers?

Nth term of the sequence of triangular numbers
The triangular numbers form a type of quadratic sequence. The nth term of the sequence is,
T_{n}=\frac{1}{2}n(n+1).To calculate a term within the sequence of triangular numbers, we substitute the position of the term into the nth term (this would be the value of n ) and calculate the resulting value.
For example,
To find the 5th triangular number, n=5, so
T_{5}=\frac{1}{2} \times 5 \times(5+1)=15.Pascal’s triangle
Pascal’s triangle shows the binomial coefficients of a binomial expansion (x+y)^{n} where the value in the row below is the sum of the two values above it.

The triangular numbers appear in Pascal’s triangle next to the natural numbers. This means that if we add these two values together, we will obtain the next triangular number below it.
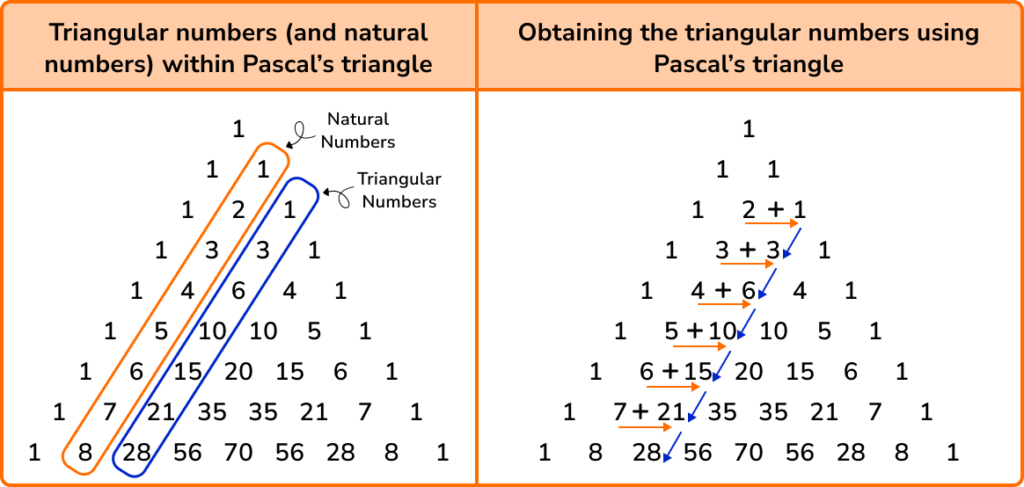
Did you know: given two consecutive triangular numbers, the sum of triangular numbers is a square number!
How to use triangular numbers
In order to calculate a triangular number, given a sequence:
- Calculate the difference between two consecutive terms.
- Add one more than this value to determine the next term.
- Continue until you reach the required term in the sequence.
Explain how to use triangular numbers

Triangular numbers worksheet

Get your free triangular numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Triangular numbers worksheet

Get your free triangular numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREETriangular numbers examples
Example 1: triangular numbers picture sequence
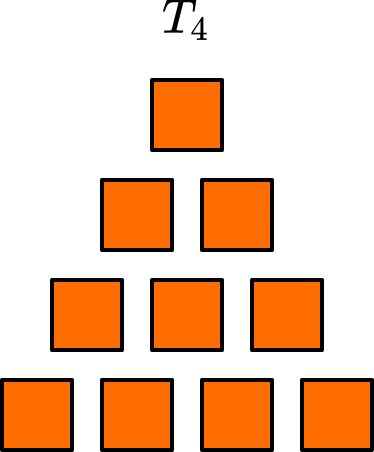
Draw the next picture in the sequence, T_{4}.
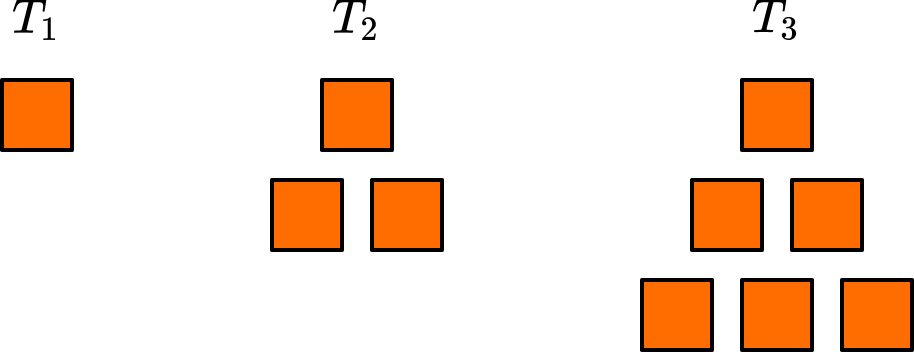
- Calculate the difference between two consecutive terms.
Term 2 contains 3 squares.
Term 3 contains 6 squares.
6-3=3.2Add one more than this value to determine the next term.
Adding one to the previous difference means that the next term will have another row added below containing 3+1=4 squares.
3Continue until you reach the required term in the sequence.
As we want to calculate the next term, we can now draw the picture.
Example 2: triangular number sequence
The first four triangular numbers are 1, 3, 6, and 10. Is 21 a triangular number?
Calculate the difference between two consecutive terms.
As we are given the first four triangular numbers, we can calculate the difference between the last two terms, and add one more than this value to get the next number in the sequence.
10-6=4
Add one more than this value to determine the next term.
Adding one to the previous difference means that the next term will be 5 more than 10.
10+5=15
Continue until you reach the required term in the sequence.
The next term will be 6 more than 15.
15+6=21
So, 21 is a triangular number.
Example 3: triangular numbers – find the position
The first four triangular numbers are 1, 3, 6, and 10. What position in the sequence is the triangular number 45?
Calculate the difference between two consecutive terms.
As we are given the first four triangular numbers, we can calculate the difference between the last two terms and add one more than this value to get the next term.
10-6=4
Add one more than this value to determine the next term.
Adding one to the previous difference means that the next term will be 5 more than 10.
10+5=15
Continue until you reach the required term in the sequence.
The next term will be 6 more than 15.
15+6=21
The next term will be 7 more than 21.
21+7=28
The next term will be 8 more than 28.
28+8=36
The next term will be 9 more than 36.
36+9=45
So, 45 is the 9th triangular number.
How to calculate triangular numbers, using the nth term
In order to calculate a triangular number, using the nth term:
- Substitute the position of the term ( \bf{n} ) into the \bf{nth} term.
\quad \;\, T_{n}=\frac{1}{2}n(n+1) - Complete the calculation.
Explain how to calculate triangular numbers, using the nth term

Example 4: finding a small value using the nth term
Calculate the 10th triangular number.
Substitute the position of the term ( \bf{n} ) into the \bf{nth} term.
The nth term for the sequence of triangular numbers is
T_{n}=\frac{1}{2}n(n+1).
Here, we want to calculate the 10th term and so n=10.
Substituting n=10 into the nth term, you have
T_{10}=\frac{1}{2}\times{10}\times(10+1) .
Complete the calculation.
The 10th term is 55.
Example 5: triangular numbers – large value using the nth term
Calculate the 50th triangular number.
Substitute the position of the term ( \bf{n} ) into the \bf{nth} term.
The nth term for the sequence of triangular numbers is
T_{n}=\frac{1}{2}n(n+1).
Here, we want to calculate the 50th term and so n=50.
Substituting n=50 into the nth term, you have
T_{50}=\frac{1}{2}\times{50}\times(50+1) .
Complete the calculation.
So, the 50th term is 1275.
How to work out if a number is a triangular number
In order to determine whether a number is a triangular number, using the nth term:
- Form an equation where the nth term is equal to the value given.
\quad \;\; \frac{1}{2}n(n+1)= \text{given value} - Multiply both sides by \bf{2} .
- Expand the brackets.
- Rearrange the equation to get a quadratic in the form ax^{2}+bx+c=0 .
- Solve the quadratic using the quadratic formula.
- Write the solution.
Explain how to work out if a number is a triangular number

Example 6: triangular numbers using the nth term
Is 120 a triangular number?
Form an equation where the nth term is equal to the value given.
The nth term of the triangular number sequence is
T_{n}=\frac{1}{2}n(n+1).
As we want to find if 120 is a triangular number, we can form the equation
\frac{1}{2}n(n+1)=120 .
Multiply both sides by \bf{2} .
Expand the brackets.
Rearrange the equation to get a quadratic in the form ax^{2}+bx+c=0 .
We need to subtract 240 from both sides of the equation so that the quadratic is equal to 0.
n^{2}+n-240=0
Solve the quadratic using the quadratic formula.
By solving the quadratic, we determine the position of the term within the sequence. If a solution is a positive integer, then 120 is a triangular number. If both solutions are not a positive integer, then 120 is not a triangular number.
The quadratic formula is
n=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a} .
For the quadratic n^{2}+n-240=0, \ a=1, \ b=1 and c=-240.
Substituting these values into the quadratic formula, we have
n=\frac{-1\pm\sqrt{1^{2}-4\times{1}\times{-240}}}{2\times{1}} .
Simplifying this, we get
n=\frac{-1\pm\sqrt{1--960}}{2}=\frac{-1\pm\sqrt{1+960}}{2}=\frac{-1\pm\sqrt{961}}{2} .
The square root of 961 is 31 and so we now have
n=\frac{-1\pm{31}}{2} .
So our solutions are n=\frac{-1+31}{2}=15 \ or \ n=\frac{-1-31}{2}=-16.
Write the solution.
As one of the solutions is a positive integer (n=15) the number 120 is the 15th term in the sequence of triangular numbers, and so 120 is a triangular number.
Common misconceptions
- The sequence is a linear sequence
The difference between two terms is considered to be common and so the next term is found by adding the difference from the previous two terms, not one more than the difference of the previous two terms.
- Confusing the position and the value of the term
The position of the term is the value of n. The value of the term is what the nth term is equal to, given the position n. This is the difference between substituting n into the nth term, or calculating the value of n using the nth term. (See examples 5 and 6).
Practice triangular number questions
1. Below is a pattern sequence.
Which picture shows the correct pattern for the term T_{5}?


![]()

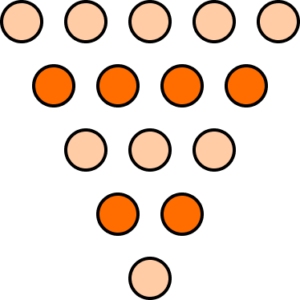

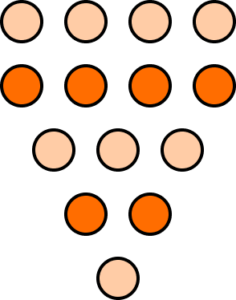

The number of ovals increases by 1 for every new row above the triangle. The new row will contain 5 ovals, above the image for T_{4}.
2. What type of number is 28?
Square Number

Decimal Number

Cube Number

Triangular Number

The sequence of triangular numbers is
1, 3, 6, 10, 15, 21, 28, …
So, 28 is a triangular number.
3. What is the position of the term 36 in the sequence of triangular numbers?
9th term

8th term

36th term

6th term

The sequence of triangular numbers is
1, 3, 6, 10, 15, 21, 28, 36, …
The position of the value 36 is the 8th term.
4. What is the value of the 12th triangular number?




Substituting n=12 into the nth term for the triangular numbers sequence, we have
T_{12}=\frac{1}{2}\times{12}\times{13}=78 .
5. What is the value of the 28th triangular number?




Substituting n=28 into the nth term for the triangular numbers sequence, we have
T_{28}=\frac{1}{2}\times{28}\times{29}=406 .
6. Which method correctly shows that 55 is a triangular number.

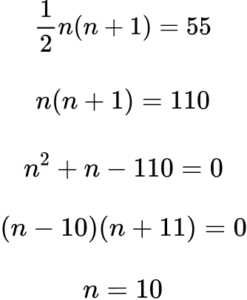

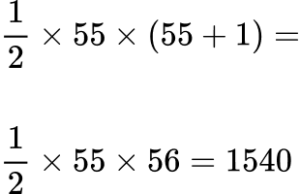

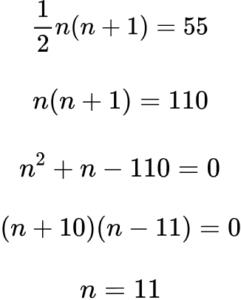

Forming an equation using the nth term of the sequence of triangular numbers, we have
\frac{1}{2}n(n+1)=55 .
Multiplying both sides of the equation by 2, we have
n(n+1)=110.Rearranging the equation to form a quadratic of the form
ax^{2}+bx+c=0 we have
n^{2}+n-110=0 .
As we can factorise 110, we do not need to use the quadratic formula. We just need to be able to solve the quadratic equation we have formed.
(n-10)(n+11)=0
The two possible solutions are
n=10\text{ or }n=-11 .
The position in a sequence must be a positive integer, so n=10.
Therefore, 55 is the 10th triangular number.
Triangular numbers GCSE questions
1. (a) The diagram below shows the number of handshakes made between an increasing number of guests at a party.
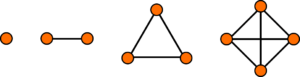
Everyone shakes hands with all of the other guests.
Draw the next pattern in the sequence.
(b) How many handshakes are given between 6 people?
(4 marks)
(a)
(1)

(1)
(b)
0, 1, 3, 6, 10, 15, 21, …
(1)
15 handshakes
(1)
2. (a) Which of the following is the nth term of the sequence of triangular numbers?
\begin{aligned} &2n^{2}+n \quad \quad \quad \quad \quad \quad \frac{n}{2}(n+1) \\\\ &\frac{1}{2}(n+1) \quad \quad \quad \quad \quad \quad n^{2}+ \frac{n}{2} \end{aligned}
(b) Show that the nth term of the sequence 1, 3, 6, 10, 15, … is \ \frac{1}{2}n(n+1).
(5 marks)
(a)
\frac{n}{2}(n+1)
(1)
(b)
Second difference =1 and so a=\frac{1}{2}.
(1)
\frac{1}{2}n^{2}=0.5, \ 2, \ 4.5, \ 8, \ 12.5, …(1)
\frac{1}{2}n=0.5, \ 1, \ 1.5, \ 2, \ 2.5, …(1)
\frac{1}{2}(n^{2}+n)=\frac{1}{2}n(n+1)(1)
3. Show that the sum of any two consecutive triangular numbers is a square number.
(5 marks)
\frac{n}{2}(n+1) \ or \ \frac{n+1}{2}(n+2)
(1)
\frac{n}{2}(n+1) \ and \ \frac{n+1}{2}(n+2)
(1)
\frac{n}{2}(n+1)+\frac{n+1}{2}(n+2)=\frac{n^{2}+n}{2}+\frac{n^{2}+3n+2}{2}(1)
=\frac{2n^{2}+4n+2}{2}=n^{2}+2n+1(1)
=(n+1)^2(1)
Learning checklist
You have now learned how to:
- Recognise and use sequences of triangular numbers
- Use the nth term of a triangular numbers sequence to solve problems
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.