GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Area of a quadrilateral Area of a triangle 3D shapes Faces, edges and vertices

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes Prism

Surface Area

Surface Area Of A Prism

Here we will learn about the surface area of a prism and how to calculate it.

There are also volume and surface area of a prism worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the surface area of a prism?

The surface area of a prism is the total area of all of the faces.

To work out the surface area of a prism, you work out the area of each face and add them all together.

Sketching each face of the prism and labelling its dimensions can help to structure the solution. Below are a few examples of prisms with their component faces.

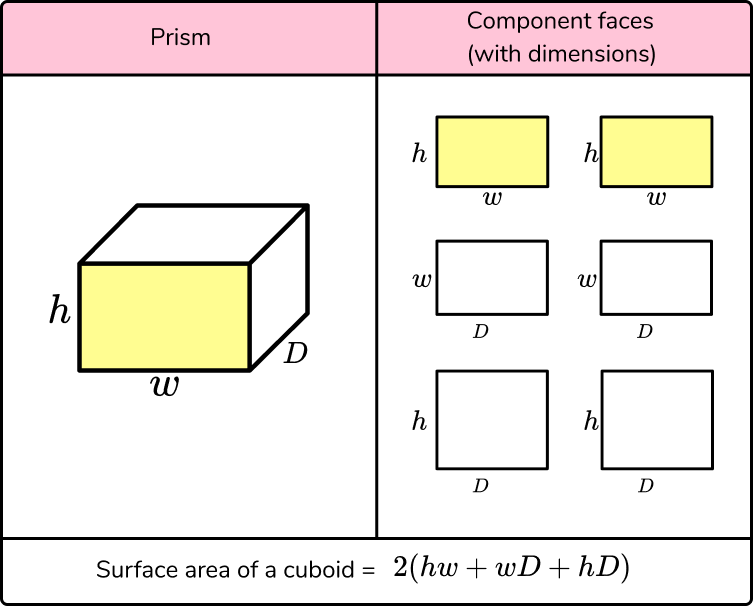
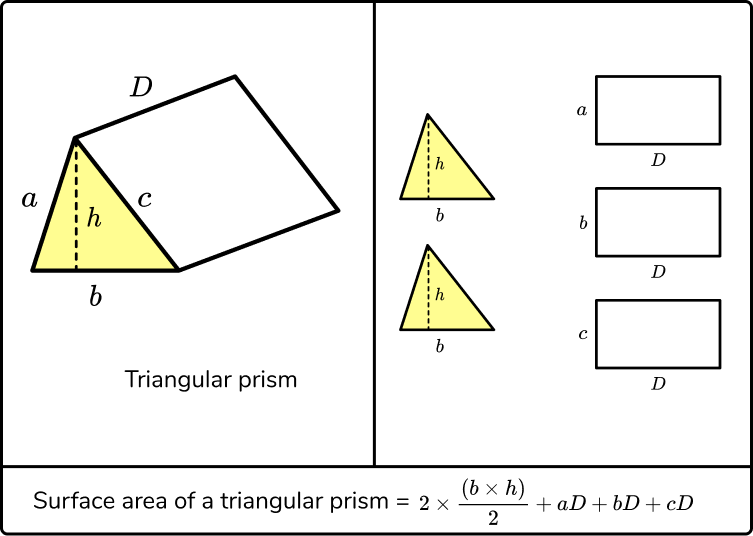
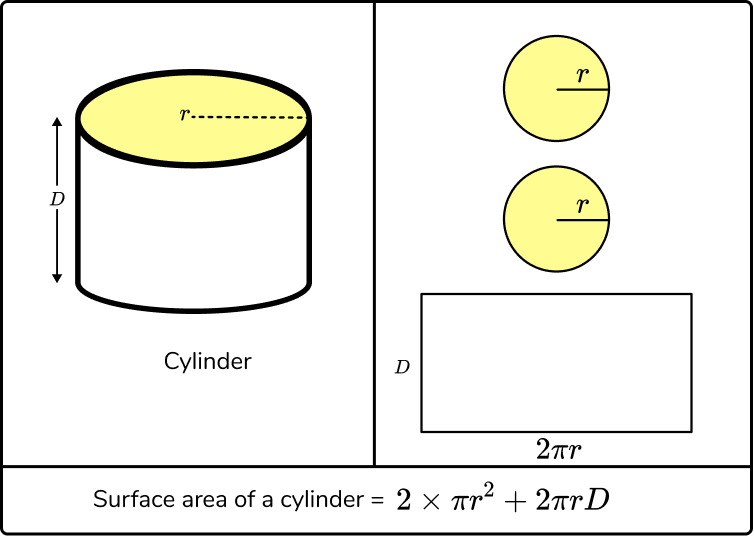
What is the surface area of a prism?

The cuboid

If we inspect a cuboid, we can see that the prism is made up of $6$ rectangular faces.

It specifically has $3$ pairs of congruent faces (not all prisms have this property) as the opposing faces are the same size.

To calculate the surface area of the cuboid, we need to calculate the area of each face, and then add them together.

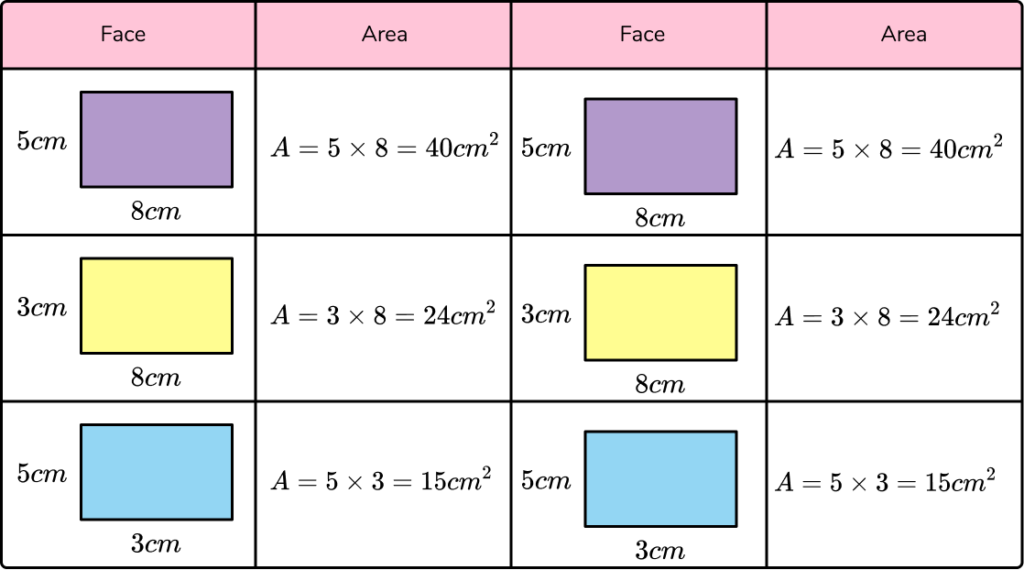
Now that we know the area of each face, the surface area of the prism is the sum of these values.

40+24+15+40+24+15=158.

The surface area of the cuboid is equal to $158cm^2$ .

Note: Surface area is measured in square units (e.c. $mm^2, cm^2, m^2$ etc).

How to calculate the surface area of a prism

In order to work out the surface area of a prism:

Work out the area of each face.
Add the area of each face together.
Write the answer, including the units.

How to calculate the surface area of a prism

Surface area of a prism worksheet

Get your free surface area of a prism worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Surface area of a prism worksheet

Get your free surface area of a prism worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Related lessons on prism shape

Surface area of a prism is part of our series of lessons to support revision on prism shape. You may find it helpful to start with the main prism shape lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Surface area of a prism examples

Example 1: surface area of a triangular prism

Work out the surface area of the prism.

Work out the area of each face.

The area of the front of the prism is $\frac{1}{2} \times 4 \times 3=6\mathrm{cm}^{2}$ . The back face is the same as the front face so the area of the back face is also $6cm^2$ .

The area of the base is $4\times2=8cm^2$ .

The area of the left side is $2\times3=6cm^2$ .

The area of the right side is $2\times5=10cm^2$ .

It will make our working clearer if we use a table.

Face	Area
Front	$\frac{1}{2} \times 4 \times 3 = 6$
Back	$6$
Bottom	$4\times 2 = 8$
Left side	$2\times 3 = 6$
Top	$2\times 5 = 10$

2Add the area of each face together.

The total surface area (SA) is $SA=6+6+8+6+10=36$ .

3Write the answer, including the units.

The measurements on this prism are in cm so the surface area will be measured in $cm^2$ .

Surface area = $36cm^2$ .

Example 2: surface area of a rectangular prism (cuboid)

Work out the surface area of the prism.

Work out the area of each face.

A cuboid has $6$ faces, with $3$ pairs of identical faces.

Face	Area
Front	$7\times 2 = 14$
Back	$14$
Bottom	$7\times 3 = 21$
Top	$21$
Left side	$2\times 3 = 6$
Right side	$6$

Add the area of each face together.

The total surface area (SA) is $SA=14+14+21+21+6+6=82$ .

Write the answer, including the units.

The measurements on this prism are in $m$ so the surface area of the prism is $82m^2$ .

Example 3: surface area of a trapezoidal prism

Work out the surface area of the prism.

Work out the area of each face.

A trapezoidal prism has $6$ faces, with identical trapeziums at either end. Notice that all of the other faces are rectangular.

Face	Area
Front	$\frac{1}{2}(8+18)\times{12}=156$
Back	$156$
Bottom	$20\times 18 = 360$
Top	$20\times 8 = 160$
Left side	$20\times 3 = 260$
Right side	$260$

Add the area of each face together.

The total surface area (SA) is $SA=156+156+360+160+260+260=1352$ .

Write the answer, including the units.

The measurements for this prism are in $cm$ .

The surface area of the prism is $1352cm^2$ .

Example 4: surface area of a parallelogram prism with different units

Work out the surface area of the prism.

Work out the area of each face.

A parallelogram prism has $6$ faces and, like a cuboid, it has $3$ pairs of identical faces. Notice that, once again, all of the other faces are rectangular.

In this example some of the measurements are in cm and some are in $m$ so before we begin we must convert the units so that they are the same. Here, we will convert all the units to metres ( $m$ ), $40cm = 0.4m$ and $50cm = 0.5m$ .

Face	Area
Front	$1.2\times 0.4 = 0.48$
Back	$0.48$
Bottom	$1.2\times 1.5 = 1.8$
Top	$1.8$
Left side	$0.5\times 1.5 = 0.75$
Right side	$0.75$

Add the area of each face together.

The total surface area (SA) is $SA=0.48+0.48+1.8+1.8+0.75+0.75=6.06$ .

Write the answer, including the units.

The measurements that we have used are in m so the surface area of the prism is $6.06m^2$ .

Surface area of a prism: alternative method

The surface area of a prism is special because all of the lateral faces are rectangles. To calculate the surface area of a prism, we calculate twice the area of the cross section and add the perimeter of the cross section multiplied by the depth of the prism.

Here we have a cuboid with a width of $4cm$ , a height of $1cm$ , and a depth of $2cm$ .

We will take the front and back faces of the cuboid as the cross section. The area of the cross section is equal to $4$ x $1 = 4cm^2$ .

As the front and back are congruent, the area of these two faces is equal to $4$ x $2=8cm^2$ .

Now, if we highlight the perimeter of the cross section, then unfold the cuboid so we can see the net, we can see that the perimeter of the cross section is the same as the height of the net.

As the lateral faces are all rectangles, the area of the lateral faces is equal to the perimeter of the cross section, multiplied by the depth of the prism.

(4+1+4+1) \times 2 = 20cm^2

Adding the area of the front and back to this value, we get $20+8=28$ .

The surface area of the cuboid is $28cm^2$ .

General case

In general, the surface area of any prism is

Surface area of a prism = $2A+PD$

where,

$A$ = Area of the cross section
$P$ = Perimeter of the cross section
$D$ = Depth of the prism

Surface area of a prism

How to calculate the surface area of a prism (alternative method)

In order to work out the surface area of a prism:

Calculate the area of the cross section.
Calculate the perimeter of the cross section.
Substitute all known values into the formula and solve.
Write the answer, including the units.

How to calculate the surface area of a prism (alternative method)

Alternative method examples

Example 5: surface area of a compound prism using alternative method

Work out the surface area of the prism.

Calculate the area of the cross section.

The cross section is an L-shape and so we need to split the shape into two rectangles, calculate the area of each rectangle, then add them together to get the area of the cross section.

Area $A$ : $2\times7=14$

Area $B$ : $7\times4=28$

The total area of cross-section is $14+28=42$ .

The area of the cross section $A=42cm^2$ .

Calculate the perimeter of the cross section.

The perimeter of the L-shape is equal to $2\times(9+7)=32cm$ .

P=32cm

Substitute all known values into the formula and solve.

Using the formula,

surface area of a prism $= 2A+PD$ ,

when $A=42$ , $P=32$ and $D=10$ , we have

\[\text{SA}=2\times{42}+(32\times{10})\\ =84+320\\ =404\]

Write the answer, including the units.

The surface area of the prism is $404cm^2$ .

Example 6: surface area of a compound prism using alternative method

Work out the surface area of the prism.

Calculate the area of the cross section.

We can split the cross section into two polygons, a rectangle and a trapezium. We then work out the area of both, and add the values together to get the area of the cross section.

Area $A$ : $5\times2=10$

Area $B$ : $\frac{1}{2}(2+5) \times 4=14$

10+14=24

The area of the cross section $A=24cm^2$ .

Calculate the perimeter of the cross section.

The perimeter of the cross section is equal to the sum of the edges of the cross section.

P=5+2+5+2+6=20cm

Substitute all known values into the formula and solve.

Using the formula,

Surface area of a prism $= 2A+PD$ ,

when $A=24, P=20$ and $D=9$ , we have

\[\text{SA}=2\times{24}+(20\times{9})\\ =48+180\\ =228.\]

Write the answer, including the units.

The surface area of the prism is $228cm^2$ .

Example 7: surface area of a trapezoidal prism using alternative method

Work out the surface area of the prism.

Calculate the area of the cross section.

The cross section is a trapezium with an area formula of $\text{A}=\frac{1}{2}(a+b)h$ .

\[A=\frac{1}{2}(a+b)h\\ =\frac{1}{2}(10+4)\times{4}\\ =28\]

$A=28cm^2$ .

Calculate the perimeter of the cross section.

The perimeter of the trapezium is the sum of the edges, $P=10+5+4+5=24cm$ .

Substitute all known values into the formula and solve.

Using the formula,

Surface area of a prism $= 2A+PD$ ,

when $A=28, P=24$ and $D=12$ , we have

\[\text{SA}=2\times{28}+(24\times{12})\\ =56+288\\ =344.\]

Write the answer, including the units.

The surface area of the trapezoidal prism is $344cm^2$ .

Common misconceptions

Calculating volume instead of surface area

Volume and surface area are different things – volume tells us the space within the shape whereas surface area is the total area of the faces. To find surface area, work out the area of each face and add them together.

Calculating with different units

You need to make sure all measurements are in the same units before calculating surface area. (You can’t have some in $cm$ and some in $m$ , for example).

Using the wrong formula

Be careful to apply the correct prism related formula to the correct question type.

Practice surface area of a prism questions

288cm^2

336cm^2

384cm^2

408cm^2

Calculating the area of each face, we have

Face	Area
Front	$\frac{1}{2}$ × 8 × 6 = 24
Back	24
Bottom	12 × 8 = 96
Left side	12 × 6 = 72
Right side	12 × 10 = 120

Total surface area $=24+24+96+72+120=336cm^{2}$ .

154mm^2

113mm^2

226mm^2

336mm^2

Work out the area of each face,

Face	Area
Front	7 × 2 = 1
Back	14
Bottom	7 × 11 = 77
Top	77
Left side	2 × 11 = 22
Right side	22

Total surface area $=14+14+77+77+22+22=226\mathrm{mm}^{2}$ .

252cm^2

330cm^2

205cm^2

246cm^2

Work out the area of each face,

Face	Area
Front	$\frac{1}{2}$ × 8 × 10.5 = 42
Back	42
Top left	5 × 6 = 30
Top right	30
Bottom left	8.5 × 6 = 51
Bottom right	51

Total surface area $=42+42+30+30+51+51=246\mathrm{cm}^{2}$ .

2658mm^2

7920mm^2

133.5mm^2

833.4mm^2

First we need to convert all of the units to millimetres.

$2.4cm=24mm$ ,
$2.5cm=25mm$ ,
$3cm=30mm$ .

Work out the area of each face,

Face	Area
Front	$\frac{1}{2}$ (15+7) × 24 = 264
Back	264
Top	25 × 30 = 750
Bottom	24 × 30 = 720
Left side	15 × 30 = 450
Right side	7 × 30 = 210

Total surface area $=264+264+750+720+450+210=2658\mathrm{mm}^{2}$ .

742cm^2

462cm^2

1020cm^2

742cm^2

Area $A$ : $5 \times 6=30$
Area $B$ : $7 \times 3=21$

The total area of cross-section is $30+21=51$ .

Work out the area of each face,

Face	Area
Front	51
Back	51
Bottom	7 × 20 = 140
Left side	9 × 20 = 180
Top 1	5 × 20 = 100
Right side 1	6 × 20 = 120
Top 2	2 × 20 = 40
Right side 2	3 × 20 = 60

Total surface area $=51+51+140+180+100+120+40+60=742\mathrm{cm}^{2}$

3210m^2

3570m^2

11700m^2

3330m^2

Area $A$ : $24 \times 30=720$
Area $B$ : $\frac{1}{2} \times 24 \times 5=60$

The total area of cross-section is $720+60=780$ .

Work out the area of each face,

Face	Area
Front	780
Back	780
Left side	30 × 15 = 450
Top	24 × 15 = 360
Right side	30 × 15 = 450
Right bottom	13 × 15 = 195
Left bottom	13 × 15 = 195

Total surface area $=780+780+450+360+450+195+195=3210\mathrm{m}^{2}$

Surface area of a prism GCSE questions

1. Work out the surface area of the prism.

(3 marks)

Show answer

Area of cross-section $=3 \times 3 + 10 \times 6=69$

(1)

The areas of rectangular faces are $180, 162, 54, 54, 126$ and $108$ .

(1)

The total surface area is $69+69+180+162+54+54+126+108=822\mathrm{cm}^{2}$

(1)

2. The two prisms shown have the same volume. Vicky says that means they also have the same surface area. Is Vicky correct? Show how you decide.

(3 marks)

Show answer

The cuboid surface area is $6+6+20+20+30+30=112\mathrm{cm}^{2}$ .

(1)

The triangular prism surface area is $6+6+30+40+50=132\mathrm{cm}^{2}$ .

(1)

No they do not have the same surface area.

(1)

3. Frank wants to paint his rabbit’s hutch. The dimensions of the hutch are shown below.

The paint that Frank wants to use covers $10$ square metres per litre.The paint comes in $100ml, 500ml$ or $1l$ tins.

Frank wants to buy the smallest tin possible.
Which tin should Frank buy? Show your working.

(4 marks)

Show answer

The area of cross-section is $\frac{1}{2}(0.5+0.75) \times 0.6=0.375$ .

(1)

The areas of other faces are $0.9, 1.125, 0.975, 0.75$ .

(1)

The total surface area is $0.375+0.375+0.9+1.125+0.975+0.75=4.5$ .

(1)

Needs to cover $4.5$ square metres so need $0.45l$ – Frank needs to buy $500ml$ .

(1)

Learning checklist

You have now learned how to:

Calculate the surface area of a prism

Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3D

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.