GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Draw and measure line segments and angles
Parts of a circleUsing compasses
This topic is relevant for:

Perpendicular Bisector
Here we will learn about perpendicular bisectors, including how to construct a perpendicular bisector of a line segment using a pencil, a ruler and compasses.
There are also constructions worksheets, which include perpendicular bisectors, based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
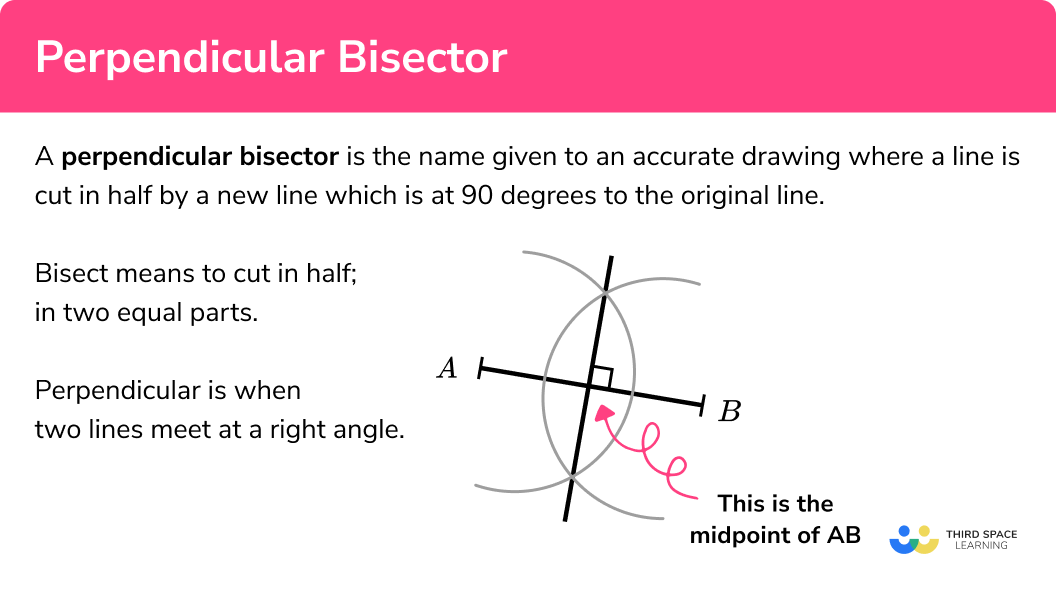
What is a perpendicular bisector?
A perpendicular bisector is the name given to an accurate drawing where a line is cut in half by a new line which is at 90 degrees to the original line.
Bisect means to cut in half, in two equal parts.
Perpendicular is when two lines meet at a right angle.
To do this we need to use a pencil, a straight-edge (a ruler) and compasses.
E.g.
Here is a perpendicular bisector of the line AB .
Arcs are drawn with compasses at the endpoints of the line segment.
A new straight line is drawn through the intersections of the arcs.
What is a perpendicular bisector?
How to construct a perpendicular bisector
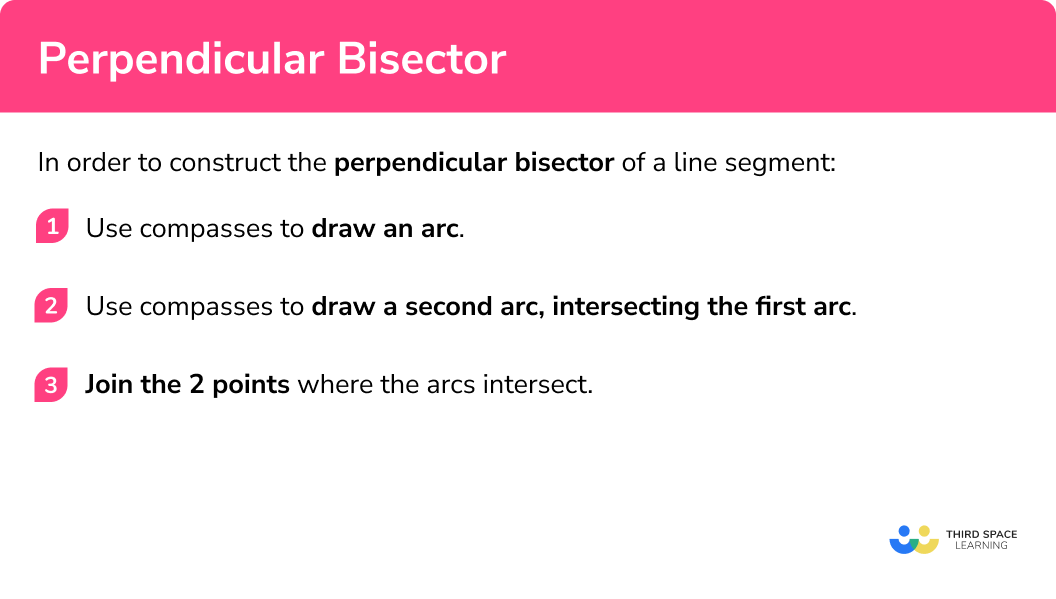
In order to construct the perpendicular bisector of a line segment:
- Use compasses to draw an arc.
- Use compasses to draw a second arc, intersecting the first arc.
- Join the 2 points where the arcs intersect.
Explain how to construct a perpendicular bisector
Perpendicular bisector worksheet

Get your free perpendicular bisector worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Perpendicular bisector worksheet

Get your free perpendicular bisector worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on constructions
Perpendicular bisector is part of our series of lessons to support revision on construction and loci and construction. You may find it helpful to start with the main loci and construction lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Perpendicular bisector examples
Example 1: perpendicular bisector
Construct a perpendicular bisector of the given line AB :
- Use compasses to draw an arc.
Open the compasses to about three-quarters of the length of the line.
Put the point of the compasses on one of the endpoints of the line.
Draw an arc:
2Use compasses to draw a second arc, intersecting the first arc.
Keeping the compasses the same, draw another arc from the other end of the line:
3Join the two points where the arcs intersect.
Using a straight-edge (a ruler), join up the two points where the arcs intersect each other:
The new line is the perpendicular bisector of the original line segment AB .
You can check that the new line goes through the midpoint of the line segment AB by using a ruler to measure. The line AB should have been cut into two equal halves.
You can also check if the lines meet at a right angle.
Example 2: perpendicular bisector
Construct a perpendicular bisector of the given line CD :
Open the compasses to about three-quarters of the length of the line.
Put the point of the compasses on one of the endpoints of the line.
Draw an arc:
Keeping the compasses the same, draw another arc from the other end of the line:
Using a straight-edge (a ruler), join up the two points where the arcs intersect each other:
The new line is the perpendicular bisector of the original line segment CD .
You can check that the new line goes through the midpoint of the line segment CD by using a ruler to measure. The line CD should have been cut into two equal halves.
You can also check if the lines meet at a right angle.
Common misconceptions
- The construction arcs must not be removed
The arcs drawn should be drawn lightly so can be adjusted if needed but they must be visible in your final answer. This is to show that you have used the correct method to draw the perpendicular bisector accurately.
- The construction arcs may be shorter
The arcs drawn may be shorter in length but they must be on both sides of the original line and must cross.
- The compasses should be set about about three-quarters of the length of the given line
The setting of the compasses is important. Too small and it makes it difficult to be accurate. It is easier for errors to be enlarged in a small space. Too large and you might not have enough space on the page to work.
- The pencil should be sharp
A sharp pencil helps your diagram to be accurate. Using a small pencil in compasses can also be helpful.
Practice perpendicular bisector questions
1. Draw a perpendicular bisector of the line CD :
2. Draw a perpendicular bisector of the line MN:
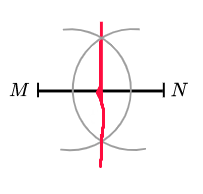




The construction arcs must be seen. The final line should go from one side of the original line to the opposite side of the line. The final line should be drawn with a straight-edge (a ruler), not drawn freehand.
Perpendicular bisector GCSE questions
1. Use ruler and compasses to construct a perpendicular bisector of the line AB.
You must show all your construction lines.
(2 marks)
(1)
(1)
2. The diagram shows the plan of a garden:
An apple tree in the garden is equidistant from S and from R .
The apple tree is exactly 5 m from Q .
On the diagram, mark the position of the apple tree with a cross (\times).
(3 marks)
For perpendicular bisector of SR
(1)
For arc of circle radius 5 cm centre Q
(1)
For the correct point
(1)
Learning checklist
You have now learned how to:
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.