GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Substitution Calculator skills Pi r squared Fractions How to work out perimeterThis topic is relevant for:

Circles, Sectors And Arcs
Here we will learn about circles, arcs and sectors, including how to find the area and circumference of a circle and how to find the area and arc length of a sector.
There are also circles, arcs and sectors worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are circles, arcs and sectors?
Circles are round plane figures whose boundaries consist of points equidistant from a fixed point.

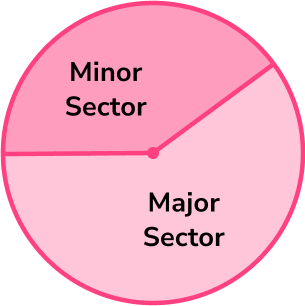
Sector of a circle
Sectors are sections of a circle that are created by two radii and an arc.
Major sector – a major sector has a central angle which is more than 180°.
Minor sector – a minor sector has a central angle which is less than 180°.
Step-by-step guide: Sector of a circle

Arc of a circle
Arcs are portions of the circumference of the circle.
Major arc – a major arc is greater than half the circumference.
Minor arc – a minor arc is less than half the circumference.
Step-by-step guide: Arc of a circle

What are circles, arcs and sectors?

Parts of a circle
The parts of a circle have specific names and properties which you need to know for all circle related questions.
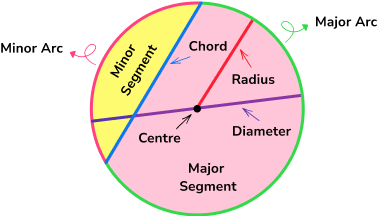
Step-by-step guide: Parts of a circle
Area and circumference of a circle
- Area of a circle (\pi r^{2})
The area of a circle can be found by multiplying the square of the radius by \pi .

For example,
The radius of a circle is 4cm.
The area of the circle is \pi \times 4^{2}=16 \pi \ \mathrm{cm}^{2}= 50.265… \mathrm{cm}^{2}
Step-by-step guide: Area and circumference of a circle
- Circumference of a circle (\pi d)
The circumference of a circle can be found by multiplying the diameter by \pi .

For example,
The diameter of a circle is 5 \ cm.
The circumference of the circle is \pi \times 5=5 \pi \ \mathrm{cm}=15.7079… cm
Step-by-step guide: Circumference of a circle
Area of a sector and arc length
- Area of a sector
The area of a sector is a part of the area of the full circle.
It can be found by using the formula \frac{\theta}{360} \times \pi r^{2}.
For example,
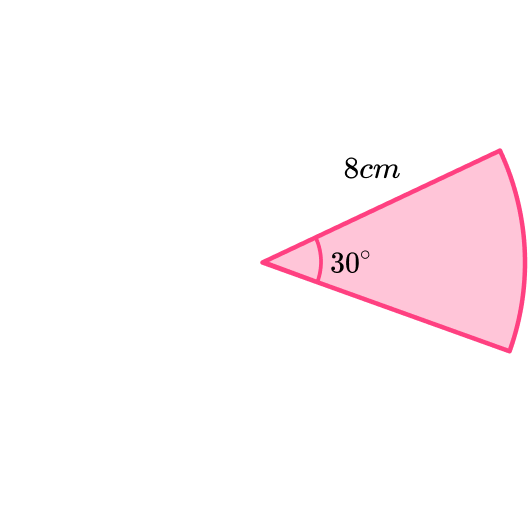
In this sector,
\theta=30^{o}, r=8 \mathrm{~cm}.The area of the sector can be found using the formula.
\begin{aligned} \text{Area of sector }&=\frac{30}{360} \times \pi \times 8^{2}\\\\ &=\frac{16}{3} \pi \ \mathrm{cm}^{2}\\\\ &=16.755… \ \mathrm{cm}^{2} \end{aligned}Step-by-step guide: Area of a sector
- Arc length
The arc of a circle is part of the circle’s circumference.
Its length can be found using the formula \frac{\theta}{360} \times \pi d.
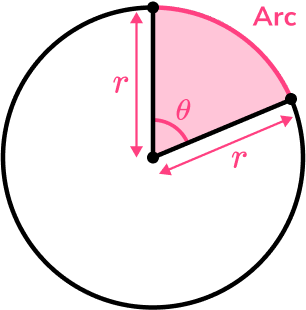
For example,
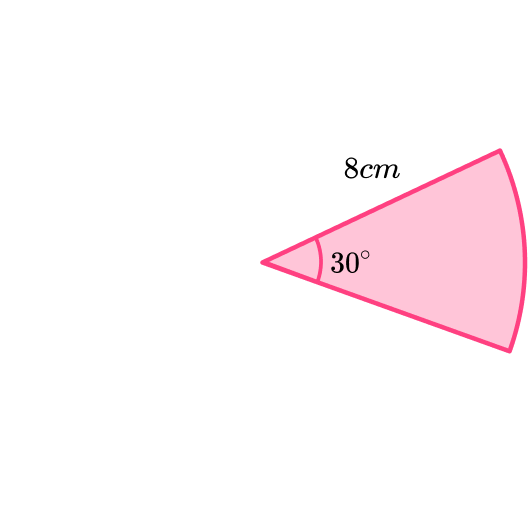
In this sector,
\theta=30^{o} and the radius is 8 \ cm. This means the diameter is 16 \ cm.
The arc length can be found using the formula.
\begin{aligned} \text{Arc length} &= \frac{30}{360} \times \pi \times 16\\\\ &=\frac{4}{3} \pi \ \mathrm{cm}\\\\ &=4.188… \ \mathrm{cm} \end{aligned}Step-by-step guide: Arc of a circle
See also: Arc length
- Perimeter of a sector
To find the perimeter of a sector you need to find the arc length and then add it to the two radii (i.e. find the length around the edge of the sector).

Step-by-step guide: Perimeter of a sector
- Segment of a circle
A segment of a circle is created when a chord is drawn within the circle.
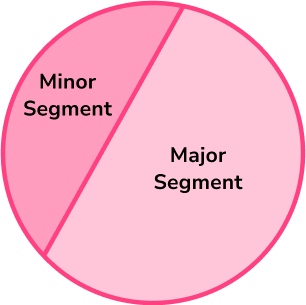
You can find the area of a segment by finding the area of the sector and subtracting the area of the triangle, as shown in the diagram below.
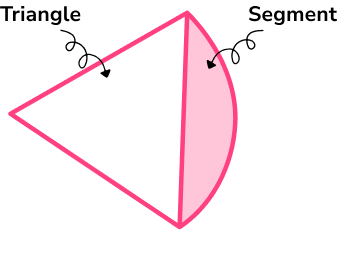
Step-by-step guide: Segment of a circle
See also: Area of a segment
Equation of a circle
- Equation of a circle
The equation of a circle (at GCSE) is given in the form
x^{2}+y^{2}=r^{2}.The circles that we study at GCSE have centre (0,0) and radius r.
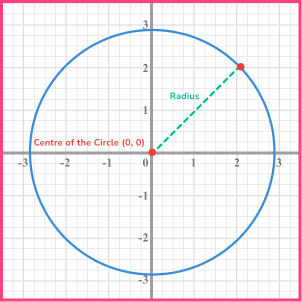
Step-by-step guide: Equation of a circle
- Equation of tangent
A tangent to a circle is a straight line which touches the circle at one point only.
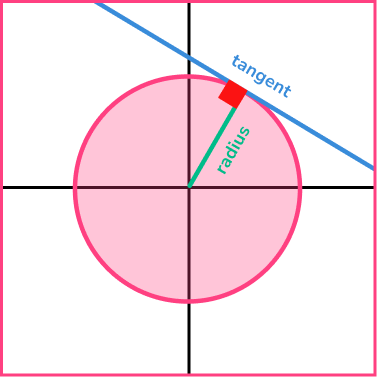
The tangent line is always perpendicular to the radius at that point. To find the equation of the tangent to a circle at a given point,
- Find the gradient of the radius at that point.
- Find the gradient of the tangent at that point.
- Substitute the x and y coordinates of the given point to find the y -intercept of the tangent, and hence the equation of the tangent line.
Step-by-step guide: Equation of tangent
Circles, Sectors, Arcs

Circles, arcs and sectors worksheet

Get your free circles, arcs and sectors worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Circles, arcs and sectors worksheet

Get your free circles, arcs and sectors worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREECircles, arcs and sectors examples
Example 1: find the radius of a circle from its diameter
Find the radius of the circle shown below.

The diagram shows the diameter of the circle as 12 \ cm.
We know the diameter is twice the length of the radius.
12 \ cm \div 2=6 \ cmThe radius of the circle is \bf{6 \ cm} .
Example 2: calculate the area of a circle
Find the area of the circle shown below. Give your answer to 1 decimal place.
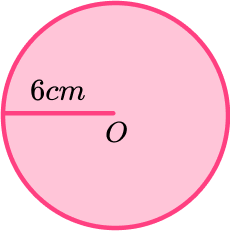
The radius is given in the diagram as 6 \ cm.
\begin{aligned} \text { Area } &=\pi r^{2} \\\\ &=\pi \times 6^{2} \\\\ &=36 \pi \\\\ &=113.0973… \end{aligned}This answer needs to be rounded to 1 decimal place and we need to include the units.
The area of the circle is
113.1 \ cm^{2}.
Example 3: calculate the circumference of a circle
Find the circumference of the circle shown below. Give your answer in terms of \pi .

We are given the diameter of the circle in the diagram as 12 \ cm.
Therefore we can calculate the circumference of the circle.
This answer is in terms of \pi so we just need to include the units.
The circumference of the circle is
12\pi \ \mathrm{cm}.
Example 4: calculate the area of a sector
Find the area of the sector shown below. Give your answer to 3 significant figures.
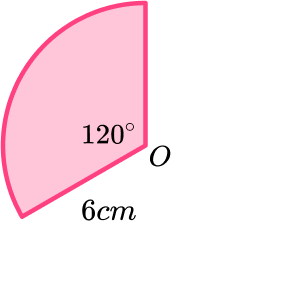
We are given the radius as 6 \ cm .
The angle of the sector is 120°.
The formula for the area of a sector of a circle is
\text{area of a sector }=\frac{\theta}{360} \times \pi r^{2}.
Therefore we can find the area of the sector,
\begin{aligned}
\text{Area }&=\frac{\theta}{360} \times \pi r^{2} \\\\
&=\frac{120}{360} \times \pi \times 6^{2} \\\\
&=12 \pi\\\\
&=37.699...
\end{aligned}
The answer needs to be rounded to 3 significant figures and we need to include the units.
The area of the sector of the circle is
37.7 \ \mathrm{cm}^{2}.
Example 5: calculate the arc length
Find the length of the arc. Give your answer in terms of pi.
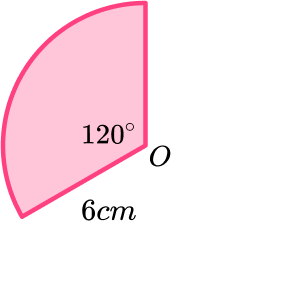
We are given the radius as 6 \ cm .
The angle of the sector is 120°.
The formula for the length of an arc is
\frac{\theta}{360} \times 2\pi r.
Therefore we can find the arc length,
\begin{aligned}
\text{Arc length }&=\frac{\theta}{360} \times 2 \pi r \\\\
&=\frac{120}{360} \times 2 \pi \times 6 \\\\
&=4 \pi
\end{aligned}
This answer is in terms of \pi so we just need to include the units.
The length of the arc is
4 \pi \ \mathrm{cm}.
Example 6: calculate the perimeter of a segment
Find the perimeter of the segment shaded in the diagram below. Give your answer to 3 significant figures.
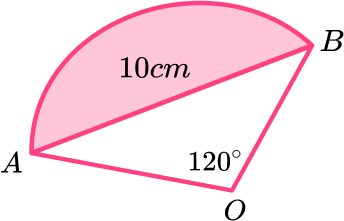
To find the perimeter you need the length of each side.
The shaded segment has two sides, the line AB and the arc. We need the length of both.
\text{Perimeter} = AB \ + \text{arc length} .
AB = 10 \ cm, we need to find out the arc length.
To find the arc length we first need to find the radius of the circle. We can use triangle ABO to help us.
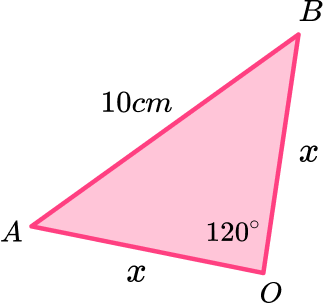
Here we can apply the cosine rule to find the lengths AO and BO. Since they are both radii, they are equal in length, so we can say that the length of each is x.
Then we can write,
\begin{aligned} a^{2}&=b^{2}+c^{2}-2 b c \cos A \\\\ 10^{2}&=x^{2}+x^{2}-2 x^{2} \cos 120 \\\\ 100&=2 x^{2}-\left(2 x^{2} \times-0.5\right) \\\\ 100&=2 x^{2}+x^{2} \\\\ 100&=3 x^{2} \\\\ \sqrt{\frac{100}{3}}&=x \\\\ \pm 5.7735 \ldots&=x \end{aligned}
x is 5.774 to 4sf, we can disregard the negative value as it is a measure of length and lengths cannot be negative.
We can now find the arc length using
Radius = 5.77 \ cm
Angle = 120°
\begin{aligned}
\text { Arc Length }&=\frac{120}{360} \times \pi \times 2(5.774) \\\\
&=12.093 \\\\
&=12.1 \ (3 \mathrm{sf})
\end{aligned}
Perimeter = AB \ + arc length
Perimeter = 10 + 12.1
Perimeter = 22.1 \ cm.
Example 7: equation of a circle
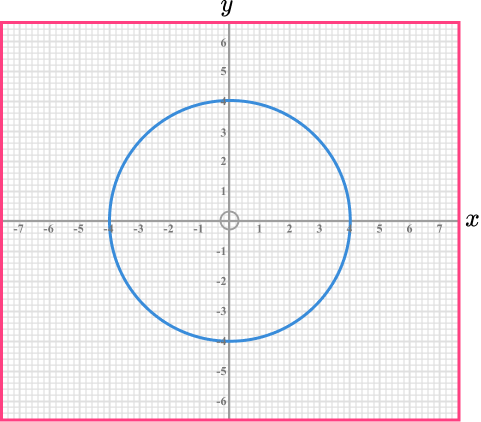
Construct the graph of x^{2}+y^{2}=16.
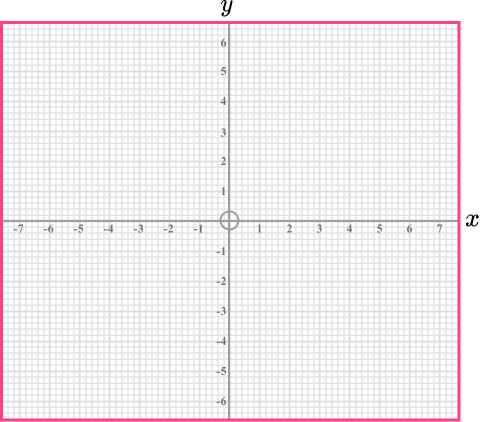
The graph x^{2}+y^{2}=16 is a circle.
The general form of the equation of a circle is x^{2}+y^{2}=r^{2} therefore r^{2}=16.
Taking the square root gives us r=4.
The graph will be a circle, centre (0, 0) and radius 4.
Example 8: equation of a tangent
The circle x^{2}+y^{2}=68 passes through the point P(8, 2).
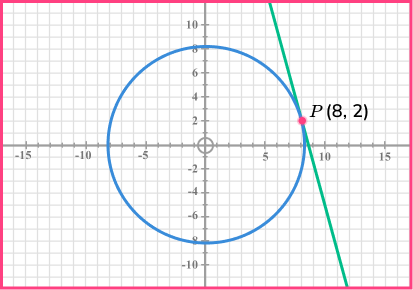
Find the equation of the tangent to the circle at the point P.
First we need to find the gradient of the radius to the point (8, 2).
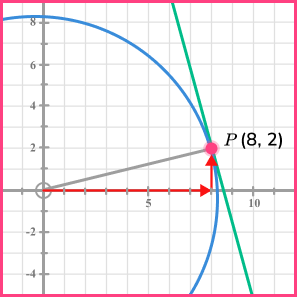
\begin{aligned}
\text{Gradient }&=\frac{\text{change in }y}{\text{change in }x}\\\\
&=\frac{2}{8}\\\\
&=\frac{1}{4}
\end{aligned}
A tangent is always perpendicular to the radius at that point, therefore the gradient of the tangent is the negative reciprocal of \frac{1}{4}.
Gradient of tangent = -4
We now know that the equation of the tangent is y=-4x+c and that the line passes through the point (8, 2).
We can find the value of c by substituting x=8 and y=2 into y=-4x+c.
\begin{aligned} y&=-4x+c\\\\ 2&=-4 \times 8 +c\\\\ 2&=-32+c\\\\ 34&=c \end{aligned}
The equation of the tangent to the circle at the point (8, 2) is y=-4x+34.
Common misconceptions
- Radius and diameters
You will notice some formulas use the radius whilst others refer to the diameter. Make sure you know which one the question gives you, this allows you to find the other if required.
- Not including the correct units
Remember the value of the radius, the diameter, the arc length and the circumference are measures of length.
The value of the area of a sector or segment are measures of area and therefore the units are squared.
- Not giving answer in terms of \textbf{π}
Sometimes the question may ask you to give the answer ‘in terms of \bf{\pi} ’. This means you do not give the numerical answer that is produced when you multiply it by \bf{\pi} .
For example,
6 \times \pi = 6 \bf{\pi} (this is an answer in terms of pi)
6 \times \pi = 18.8495592… (this answer is not in terms of pi)
- Misuse of calculator
Ensure you know how to correctly use the \pi button on your calculator.
Practice circles, sectors and arcs questions
1. What is the radius of the circle?





The radius is half the diameter.
The diameter is given on the diagram as 10 \ cm.
10 \div 2=5
Radius = 5 \ cm
2. What is the area of the circle? Give your answer in terms of pi.





For this circle, the radius is 5 \ cm.
\begin{aligned} \text { Area } &=\pi r^{2} \\\\ &=\pi \times 5^{2} \\\\ &=25 \pi \end{aligned}Units are cm^{2}.
3. What is the circumference of the circle? Give your answer to 1 decimal place.





Units are cm.
4. What is the area of the sector? Give your answer in terms of pi.
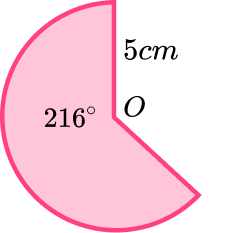




The radius is 5 \ cm and the angle of the sector is 216°.
\begin{aligned}
\text{Area }&=\frac{\theta}{360} \times \pi r^{2} \\\\
&=\frac{216}{360} \times \pi \times 5^{2} \\\\
&=15 \pi \\\\
\end{aligned}
Units are for area so are cm^{2}.
5. What is the length of the major arc? Give your answer to 3 significant figures.
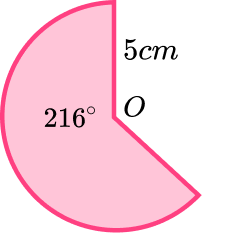




Units are for a length so are cm.
6. What is the perimeter of the sector? Give your answer correct to 1 decimal place.
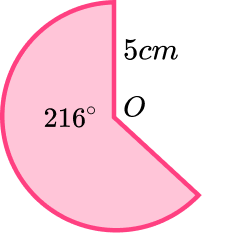




Arc length = 6 \pi (see Q5)
The perimeter of a sector is the length of the two radii plus the arc length.
Therefore the perimeter is
6 \pi + 5+5=28.84955…
Perimeter is a measure of length so the units are cm.
Perimeter =28.8 \ cm
7. Calculate the area of the shaded segment. Give your answer to 3 significant figures.
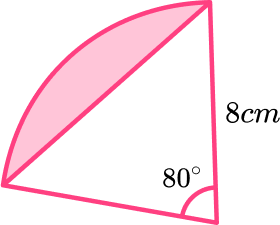




First we need to calculate the area of the sector.
\begin{aligned} \text{Area of sector }&=\frac{80}{360} \times \pi \times 8^{2}\\\\ &=\frac{128}{9} \pi \end{aligned}
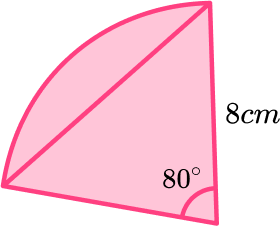
Next we need the area of the triangle. To calculate this we can use
\text{Area of triangle }=\frac{1}{2}ab \sin C.

We get,
\begin{aligned} \text{Area of triangle }&=\frac{1}{2} \times 8 \times 8 \times \sin (80) \\\\ &=31.5138… \end{aligned}
Finally we can subtract the area of the triangle from the area of the sector.
\begin{aligned}
\text{Area of segment }&=\frac{128}{9} \pi -31.5138… \\\\
&=13.16658…
\end{aligned}
The area of the segment is 13.2cm^2 \ (3sf).
8. A circle, centre (0, 0), has a radius of 9. What is the equation of the circle?




The general form for the equation of the circle is x^{2}+y^{2}=r^{2}.
Here r=9 and therefore r^{2} = 81 and x^{2}+y^{2}=81.
Circles, sectors and arcs GCSE questions
1. Look at the diagram below showing a circle.

(a) What is the radius of the circle?
(b) Calculate the area of the circle. Give your answer to 1 decimal place.
(c) Calculate the circumference of the circle. Give your answer to 1 decimal place.
(5 marks)
(a)
8 \ cm
(1)
(b)
\pi \times 8 \times 8 \ oe \ or \ 201.06…
(1)
201.1(1)
(c)
\pi \times 16
(1)
50.3(1)
2. OAB is a sector of a circle.
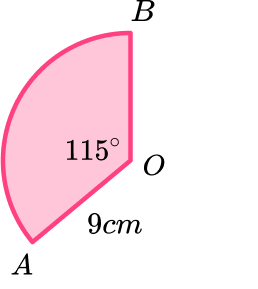
(a) Calculate the area of the sector.
Give your answer to 3 significant figures.
(b) Calculate the length of the arc AB.
Give your answer to 3 significant figures.
(c) Calculate the perimeter of the sector.
Give your answer to 3 significant figures.
(9 marks)
(a)
\frac{115}{360}
(1)
\frac{115}{360} \times \pi \times 9^{2}(1)
81.2887…(1)
81.3(1)
(b)
\frac{115}{360} \times \pi \times 18
(1)
18.064…(1)
18.1(1)
(c)
“18.1” + 18 \ ft
(1)
36.1(1)
3. The area of a circle is 36\pi.
Find the radius of the circle.
(2 marks)
(1)
r=6(1)
4. A circle has the equation x^{2}+y^{2}=10.
(a) Show that the point P (-3, 1) lies on the circle.
(b) Find the equation of the tangent to the circle at the point (-3, 1).
(6 marks)
(a)
(-3)^{2}+(1)^{2}=10
(1)
9+1=10 therefore (-3, 1) lies on the circle.
(1)
(b)
Gradient of radius =-\frac{1}{3}
(1)
Gradient of tangent = 3
(1)
y=3x+c(1)
c=10 \ so \ y=3x+10
(1)
Learning checklist
You have now learned how to:
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.