GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Rearranging equations Plotting graphs Gradient of a lineThis topic is relevant for:
Equation Of A Line
Here we will learn about the equation of a line, including recognising the gradient and y-intercept of a straight line, and finding the equation of a line from a graph.
There are also worksheets on the equation of a line based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is the equation of a line?
The equation of a line is the algebraic representation of a line using cartesian coordinates.
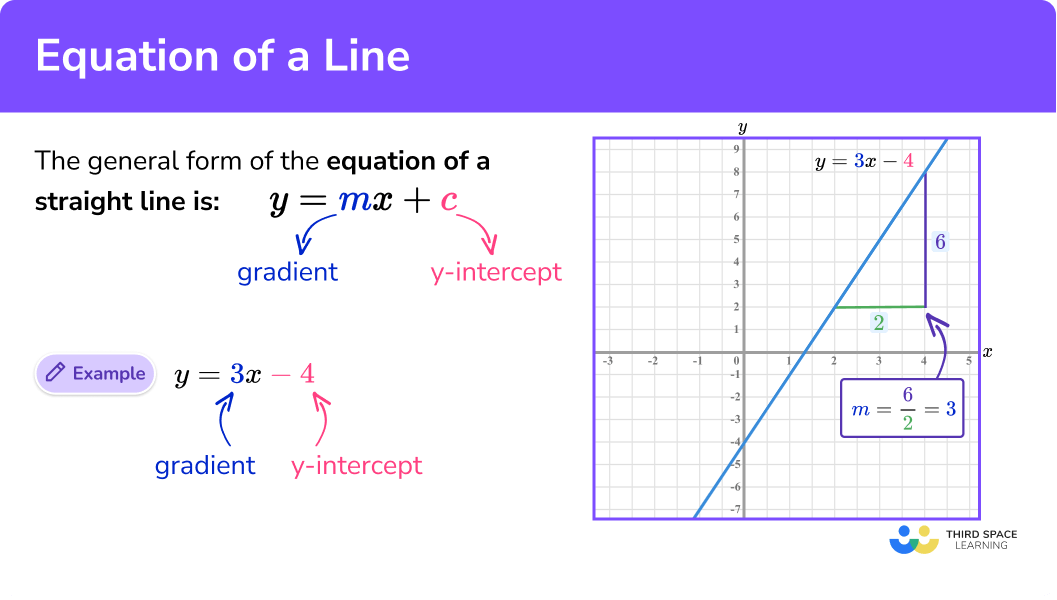
The general form of the equation of a straight line is written as y = mx + c .
Where m is the gradient of the straight line
and c is the y -intercept of the straight line.
The coordinate ( x,y) lies on the line y = mx + c giving us a linear relationship between x and y . The term linear equation is given to any straight line.
E.g.
Let’s look at the line y = 3x − 4 .
Here, we can find any y -coordinate given the value for x by substituting into the equation y = 3x − 4 .
E.g.
When x = 1 ,
So when the x value is 1 and the y value is -1 , this gives us the coordinate ( 1, -1 ) which lies on the line as shown below.
Not all straight lines will appear to be exactly in the form y = mx + c so we need to understand how we determine the gradient (or steepness of the line) m , and the y -intercept (the point where the line intersects the y -axis) c from equations that are not in the form y = mx + c .
Here are some examples of linear equations not in the form y = mx + c
- y + 17 = 6x
- 2y = 10x + 3
- x = 6y −1
- y = −3 (a horizontal line)
- x = y
- x = 0 (a vertical line)
In order to easily determine m and c we need to rearrange the equation to make y the subject.
E.g.
Take the equation above of y + 17 = 6x and make y the subject.
By rearranging the equation into the form y = mx + c we can clearly state that the gradient m = 6 and the y -intercept c = −17 .
From this, we can draw the straight line onto a set of axes.
What is the equation of a line?
How to find the equation of a line
In order to find the equation of a straight line:
- Calculate the gradient of the line
- State the y -intercept of the straight line
- Write the equation of the line in the form y = mx + c
Explain how to find the equation of a line
Equation of a line worksheet
Get your free equation of a line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE Equation of a line worksheet
Get your free equation of a line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on straight line graphs
Equation of a line is part of our series of lessons to support revision on straight line graphs. You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Equation of a line examples
Example 1: Positive gradient, positive y -intercept
Work out the equation of the straight line given in the diagram below.
- Calculate the gradient of the line.
Two points that lie on the line are: ( 0, 4 ) and ( 2, 8 ).The line passes through these two given points.
So the gradient
\begin{aligned} &m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{8-4}{2-0}=\frac{4}{2}=2\\\\ &m=2 \end{aligned}2State the
The y -intercept occurs when x = 0 .
Here, c = 4
3Write the equation of the line in the form y = mx + c .
As the slope m = 2 and y intercept c = 4 ,
y=2x+4Example 2: Positive gradient, negative y -intercept
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( 1, −4 ) and ( 3, 2 ).
So the gradient
\begin{aligned}
&m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2--4}{3-1}=\frac{6}{2}=3\\\\
&m=3
\end{aligned}
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Here, c = −7
Write the equation of the line in the form y=mx+c .
As m = 3 and c = −7, y = 3x − 7
Example 3: Negative gradient, positive y -intercept
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( 1, −2 ) and ( −1, 8 ).
So the gradient
\begin{aligned}
&m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{8--2}{-1-1}=\frac{10}{-2}=-5\\\\
&m=-5
\end{aligned}
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
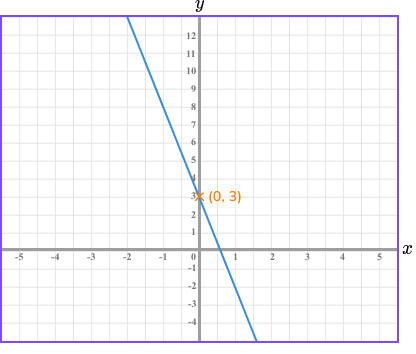
Here, c = 3
Write the equation of the line in the form y=mx+c .
As m = −5 and c = 3, y = −5x + 3
Example 4: Negative gradient, negative y -intercept
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( −3, −2 ) and ( 2, −7 ).
So the gradient
\begin{aligned}
&m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-7--2}{2--3}=\frac{-5}{5}=-1\\\\
&m=-1
\end{aligned}
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Here, c = −5
Write the equation of the line in the form y=mx+c .
As m = −1 and c = −5, y = −x − 5
Example 5: Positive fractional gradient, positive y -intercept
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( 4, 10 ) and ( −2, 7 ).
So the gradient
\begin{aligned}
&m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{7-10}{-2-4}=\frac{-3}{-6}=\frac{1}{2}\\\\
&m=\frac{1}{2}
\end{aligned}
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Here, c = 8
Write the equation of the line in the form y=mx+c .
As m = \frac{1}{2} and c = 8, \;y = \frac{1}{2}x + 8
Example 6: Negative fractional gradient, negative y -intercept
Work out the equation of the straight line given in the diagram below.
Calculate the gradient of the line.
Two points that lie on the line are: ( −2, −4 ) and ( 2, −5 ).
So the gradient
\begin{aligned} &m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-5--4}{2--2}=\frac{-1}{4}\\\\ &m=\frac{-1}{4} \end{aligned} .
State the y -intercept of the straight line.
The y -intercept occurs when x = 0 .
Here, c = -4.5 or c=-\frac{9}{2} .
Write the equation of the line in the form y=mx+c .
As m=-\frac{1}{4} and c=-\frac{9}{2}, \;y=-\frac{1}{4}x-\frac{9}{2} .
Common misconceptions
- Mixing up the gradient and the y -intercept
The coefficient of x is the gradient m and the constant term is the y -intercept c . If the coefficient of x is 1 , remember this is written as x only as 1x = x .
- The gradient is positive or negative
Ignoring the negative values in a coordinate means that the gradient will be calculated incorrectly. When picking two coordinates, make sure that the coordinates go through the corner of a grid square. If there are negative values, make sure you use them with the negative symbol.
- Mixing up the coordinates
When calculating the gradient of a straight line, be careful to not mix up the coordinates.
E.g.
Looking back at example 5 , we have the two points that lie on the line being ( 1, −2 ) and ( −1,8 ).
The change in y could be correctly calculated as 8 \; − \; −2 but the change in x is then incorrectly calculated as 1 \; − \; −1 . This would result in the gradient of the line being 5 and not −5 .
Correct answer: m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{8--2}{-1-1}=\frac{10}{-2}=-5
- Incorrect change in x or y
Avoid counting squares to work out the change in x or y . Use the axes scales or label the coordinates, then find the difference between them.
- Not calculating the gradient
A common error is to not calculate the gradient of the line.
Let’s look at example 1 ,
A error could be made by identifying the y -intercept and determining that the equation of the line is y = x + 4 .
This will only work when x = 0 but not for any other value for x .
Practice equation of a line questions
1. Work out the equation of the straight line
Two coordinates: (0,1) and (2,11)
m=\frac{11-1}{2-0}=\frac{10}{2}=5
c=1
2. Work out the equation of the straight line
Two coordinates: (0,-8) and (1,-2)
m=\frac{-2- -8}{1-0}=\frac{6}{1}=6
c=-8
3. Work out the equation of the straight line
Two coordinates: (2,0) and (1,5)
m=\frac{5-0}{1-2}=\frac{5}{-1}=-5
c=10
4. Work out the equation of the straight line
Two coordinates: (3,-3) and (4,-4)
m=\frac{-4- -3}{4-3}=\frac{-1}{1}=-1
c=0
5. Work out the equation of the straight line
Two coordinates: (0,2) and (3,4)
m=\frac{4-2}{3-0}=\frac{2}{3}
c=2
6 Work out the equation of the straight line
Two coordinates: (3,-8) and (-3,-5)
m=\frac{-5- -8}{-3-3}=\frac{3}{-6}=-\frac{1}{2}
c=-\frac{13}{2}
Equation of a line GCSE questions
1. Here is the graph of a straight line.
Work out the equation of the line in the form y=mx+c.
(3 marks)
Two coordinates: (12,-2) and (0,6) and Gradient m=\frac{6- -2}{0-12}=\frac{8}{-12}=-\frac{3}{4}
(1)
c=6
(1)
y=-\frac{3}{4}x+6
(1)
2. (a) Calculate the slope of the line in the diagram below.
(b) Show that the equation of the line is the same as \frac{1}{2}y=x+2.
(4 marks)
(a)
Two coordinates: (0,4) and (2,8) and Gradient m=\frac{8-4}{2-0}=\frac{4}{2}=2
(1)
(b)
c=4
(1)
y=2x+4
(1)
(1)
3. The two straight lines A and B are parallel. The equation of line A is y=\frac{1}{2}x+7.
Given that equation B passes through the coordinate (4,3) , work out the equation of the straight line, B .
(4 marks)
Parallel line so m=\frac{1}{2}
(1)
At (4,3), \; 3=4\times\frac{1}{2}+c
(1)
c=1
(1)
y=\frac{1}{2}x+1
(1)
Learning checklist
You have now learned how to:
- Reduce a given linear equation in 2 variables to the standard form y = mx + c ; calculate and interpret gradients and intercepts of graphs of such linear equations numerically, graphically and algebraically
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.