FREE DOWNLOAD
Volume And Surface Area Of A Cone Worksheet
Help your students prepare for their Maths GCSE with this free volume and surface area of cones worksheet of 34 questions and answers
- Section 1 of the volume and surface area of cones worksheet contains 27 skills-based volume and surface area of cones questions, in 3 groups to support differentiation
- Section 2 contains 4 applied volume and surface area of cones questions with a mix of worded problems and deeper problem solving questions
- Section 3 contains 3 foundation and higher level GCSE exam style volume and surface area of cones questionsΒ
- Answers and a mark scheme for all volume and surface area of cones questions are provided
- Questions follow variation theory with plenty of opportunities for students to work independently at their own level
- All questions created by fully qualified expert secondary maths teachers
- Suitable for GCSE maths revision for AQA, OCR and Edexcel exam boards
Unlock access to download your free resource
You can unsubscribe at any time (each email we send will contain an easy way to unsubscribe). To find out more about how we use your data, see our privacy policy.
Raise maths attainment across your school with hundreds of flexible and easy to use GCSE maths worksheets and lessons designed by teachers for teachers.
Volume and surface area of cones at a glance
A cone is a 3d shape. It has a circular base and one continuous face which tapers to a point, often referred to as the apex. The apex of a right circular cone is directly above the centre of the circular base.
To find the volume of a cone we use the formula: V = one thirdβΟr2βh where r is the radius of the base of the cone, and h is the perpendicular height of the cone.Β
For example, the volume of the cone with radius r=3cm and height h=10cm is V=30Ο.
To find the total surface area of a cone, we find the area of each face and add them together. The area of the base of the cone is found using the formula: A = Οβr2 . The curved surface area of a cone is found using the formula: A = Οrl, where r is the radius of the base and l is the slant height of the cone. These areas are then added to give the total surface area of the cone. Note, if you flatten the curved surface area of the cone, you will get a major sector of a circle with radius l (the slant height of the cone).
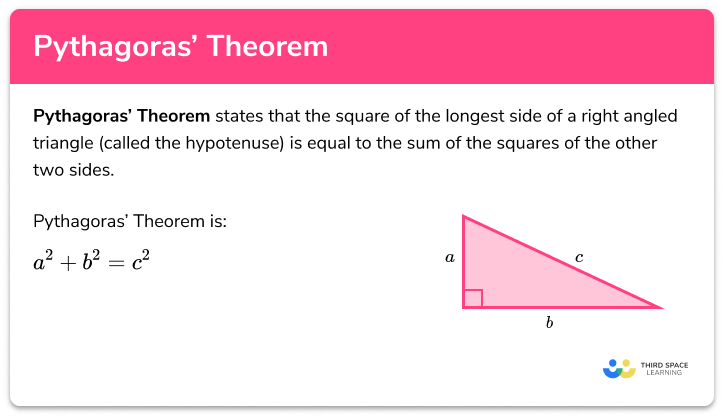
If we do not know the slant height l of the cone, we can use Pythagorasβ Theorem where the base of the right-angled triangle is the radius of the base of the cone, and the perpendicular height of the right-angled triangle is the height of the cone.
Looking forward, students can then progress to additionalΒ 3D shapes worksheets and more geometry worksheets, for example anΒ angles in polygons worksheetΒ orΒ how to calculate volume worksheet.
For more teaching and learning support on Geometry our GCSE maths lessons provide step by step support for all GCSE maths concepts.
Do you have students who need additional support?
With Third Space Learning's secondary maths tutoring programmes, students in Year 7-11 receive regular one to one maths tutoring to address gaps, build confidence and boost progress.
"My confidence in the tutoring is high. We've had some phenomenal results. I even had one girl get a Grade 8 this year; she came to every tutoring session."
Stacey Atkins, Maths Director, Outwood Grange Academies Trust