Directly Proportional Graph/Inversely Proportional Graph Worksheet

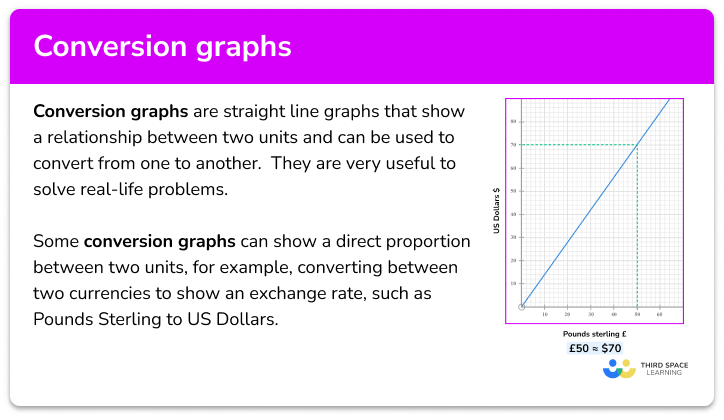
Directly proportional graph/ Inversely proportional graph at a glance

If two amounts are proportional then the ratio between them is always the same. There are two types of proportionality; direct or inverse (indirect). For direct proportion, as one amount increases so does the other, e.g. converting currency. For inverse proportion, as one amount increases the other decreases, e.g. the number of hours to complete a task assigned to multiple people. 

We can draw graphs to represent proportional relationships. Graphs showing direct proportion will always pass through the origin. Their shape will depend on the nature of the relationship. If y is directly proportional to x then the graph will be a straight line. The gradient of the straight line is the rate of change, known as the constant of proportionality, k. A good real life example of this is a currency conversion graph, where the gradient is equal to the exchange rate. 

If y is directly proportional to x2 then the graph will take the shape of a quadratic graph. 

If y is inversely proportional to x, then y is proportional to 1 divided by x. The shape of a graph showing inverse proportion is that of a reciprocal graph. 

We can read and find missing values from proportion graphs and use these to solve proportion problems.

Looking forward, students can then progress to additional ratio and proportion worksheets, for example a ratio worksheet or a ratio worksheet.

For more teaching and learning support on Ratio and Proportion our GCSE maths lessons provide step by step support for all GCSE maths concepts.