GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Arithmetic How to calculate volume Units of measurement Converting metric units

This topic is relevant for:

GCSE Maths Ratio and Proportion Compound Measures MDV

Density

Formula For Density

Here we will learn about the formula for density, including how to calculate density, mass and volume and how to solve problems involving these measures.

There are also formula for density worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the formula for density?

The formula for density is:

\text{Density}=\frac{\text{mass}}{\text{volume}}.

“Density equals mass divided by volume.”

Density is a compound measure which tells us about the mass of an object in relation to its volume.

For example, if an object has a mass of $500 \ kg$ and a volume of $2.5$ cubic metres then the density would be

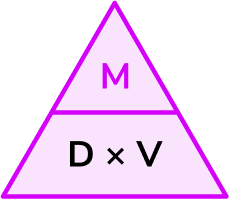
\text{Density } = \text{ mass } \div \text{ volume } = 500 \div 2.5 = 200 \ kg/m^{3}.

The density formula can be rearranged to calculate mass or calculate volume given the other two measures. An easy way to remember the formula and the different rearrangements is to use this density mass volume triangle.

From this triangle we can work out how to calculate each measure. We can “cover up” what we are trying to find and the formula triangle tells us what calculation to do.

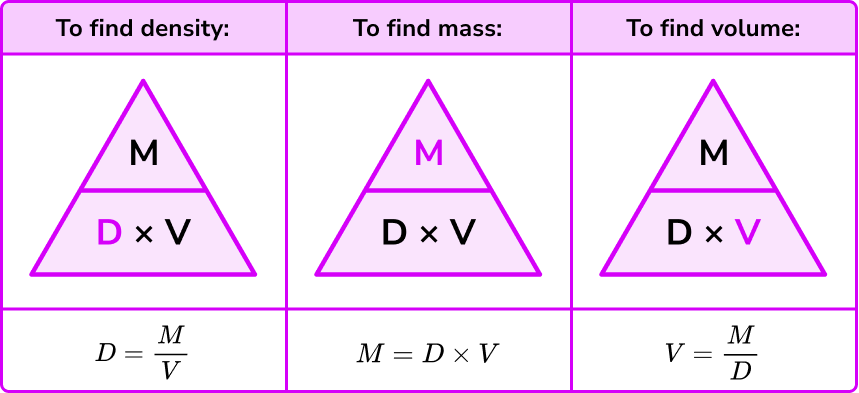
For example, if an object that has a density of $750 \ kg/m^{3}$ and a mass of $225 \ kg$ then its volume would be

\text{Volume } = \text{ mass } \div \text{ density } = 225 \div 750 = 0.3 \ m^{3}.

For example, if an object that has a density of $6.8 \ g/cm^3$ and a volume of $2.7 \ g/cm^3,$ then its mass would be

\text{Mass } = \text{ density } \times \text{ volume } = 6.8 \times 2.7 = 18.36 \ grams.

What is the formula for density?

Density, mass, volume and units of measure

Density is a compound measure and therefore involves two units; a combination of a mass in relation to volume.

It is very important to be aware of the units being used when using the density formula to calculate density, mass or volume.

Examples of units of mass: grams $(g),$ kilograms $(kg),$ milligrams $(mg).$
Examples of units of volume: cubic centimetres $(cm^{3}),$ cubic metres $(m^{3}),$ litres $(l),$ millilitres $(ml).$
Examples of units of density: grams per cubic centimetre $g/cm^{3},$ kilograms per cubic metre $kg/m^{3}.$

When you use the formula for density you must check that each measure is in the appropriate unit before you carry out the calculation. Sometimes you will need to convert a measure into different units. Here are some useful conversions to remember;

Units of Mass:

1 \ g = 1000 \ mg

1 \ kg = 1000 \ g

Units of Volume:

1\ m^{3}=1000000\ cm^{3}

1 \ litre = 1000 \ ml

1 \ ml=1 \ cm^{3}

1 \ litre = 1000 \ cm^{3}

For example, let’s calculate the density of an object that has a mass of $5300 \ g$ and a volume of $0.02$ cubic metres.

For density the units that should be used are $kg/m^{3}$ or $g/cm^{3}.$

The units given in this question are $g$ and $m^{3}$ so we need to convert one of them.

1000 \ g = 1 \ kg

Therefore,

5300 \ g = 5.3 \ kg.

Then we can calculate the density in $kg/m^{3},$

\text{Density } = \text{ mass } \div \text{ volume } = 5.3 \div 0.02 = 265\ kg/m^{3}.

Note also that sometimes you may need to convert an answer into different units at the end of a calculation.

Density in science

Using the formula for density we can calculate the density of a variety of things such as the density of a material, the density of liquid, the density of air. The greek letter $\rho$ (pronounced ‘rho’) is sometimes used to represent density.

In science there is an international system of units, known by the abbreviation SI.

This is the most modern form of the metric system and is most commonly used across the world.

The SI unit for mass is kilograms $(kg).$

The SI unit for length is metres $(m).$

The SI unit for volume is cubic metres $(m^{3}).$

These units would then calculate a density in kilograms per cubic metre $(kg/m^{3}).$ However the density unit of grams per cubic centimetres $(g/cm^{3})$ is often used.

How to use the formula for density

In order to use the formula for density to calculate density, mass or volume:

Write down the values of the measures you know with the units.
Write down the formula you need to use from the density, mass, volume triangle.
Check that the units are compatible with each other, converting them if necessary.
Substitute the values into the selected formula and carry out the resulting calculation.
Write your final answer with the required units.

Explain how to use the formula for density

Density worksheet (includes formula for density)

Get your free formula for density worksheet of 20+ density questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Density worksheet (includes formula for density)

Get your free formula for density worksheet of 20+ density questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on compound measures

Formula for density is part of our series of lessons to support revision on compound measures. You may find it helpful to start with the main compound measures lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Formula for density examples

Example 1: calculating density

A bar is made from aluminium.

It has volume $50\ cm^{3}$ and mass $135 \ g.$

Calculate the density of the object.

Write down the values of the measures you know with the units.

\text{Density } = \ ?

\text{Mass } = 135 \ g

\text{Volume } = 50 \ cm^{3}

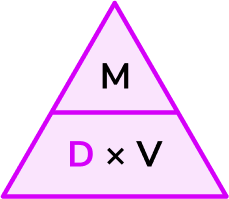
2Write down the formula you need to use from the density, mass, volume triangle.

We want to calculate density.

\text{Density}=\frac{\text{mass}}{\text{volume}}

3Check that the units are compatible with each other, converting them if necessary.

The units are $g$ and $cm^{3}$ which are compatible to calculate a density in $g/cm^{3}.$

4Substitute the values into the selected formula and carry out the resulting calculation.

\text{Density}=\frac{\text{mass}}{\text{volume}}=\frac{135}{50}=2.7

5Write your final answer with the required units.

2.7 \ g/cm^{3}

Example 2: calculating density

A block of ice has a volume of $576 \ cm^{3}$ and a mass of $530 \ g.$

Calculate the density of the ice.

Give your answer to $3$ significant figures.

Write down the values of the measures you know with the units.

\text{Density } = \ ?

$\text{Mass } = 530 \ g$

$\text{Volume } = 576\ cm^{3}$

Write down the formula you need to use from the density, mass, volume triangle.

We want to calculate density.

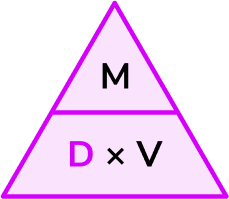
$\text{Density}=\frac{\text{mass}}{\text{volume}}$

Check that the units are compatible with each other, converting them if necessary.

The units are $g$ and $cm^{3}$ which are compatible to calculate a density in $g/cm^{3}.$

Substitute the values into the selected formula and carry out the resulting calculation.

\text{Density}=\frac{\text{mass}}{\text{volume}}=\frac{530}{576}=0.920138….

Write your final answer with the required units.

$0.920 \ g/cm^{3}$ (to 3 sf)

Example 3: calculating volume

A student weighs a piece of granite and records its mass as $800 \ g.$ The teacher tells the student that the density of the granite is $2.5\ g/cm^{3}.$

Using this information, calculate the volume of the piece of granite.

Write down the values of the measures you know with the units.

\text{Density } = 2.5 \ g/cm^{3}

$\text{Mass } = 800 \ g$

$\text{Volume } = \ ?$

Write down the formula you need to use from the density, mass, volume triangle.

We want to calculate volume.

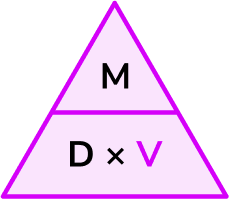
$\text{Volume}=\frac{\text{mass}}{\text{density}}$

Check that the units are compatible with each other, converting them if necessary.

The units are $g$ and $g/cm^{3}$ which are compatible to calculate a volume in $cm^{3}.$

Substitute the values into the selected formula and carry out the resulting calculation.

\text{Volume}=\frac{\text{mass}}{\text{density}}=\frac{800}{2.5}=320

Write your final answer with the required units.

320 \ cm^{3}

Example 4: calculating volume with unit conversion

The mass of an object is $2.8 \ kg.$ The object is made of a substance which has a density of $5.2 \ g/cm^{3}$ .

Calculate the volume of the object.

Give your answer to $1$ significant figure.

Write down the values of the measures you know with the units.

\text{Density } = 5.2 \ g/cm^{3}

$\text{Mass } = 2.8 \ kg$

$\text{Volume } = \ ?$

Write down the formula you need to use from the density, mass, volume triangle.

We want to calculate volume.

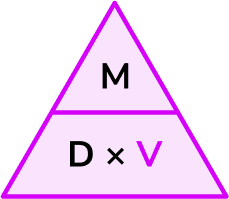
$\text{Volume}=\frac{\text{mass}}{\text{density}}$

Check that the units are compatible with each other, converting them if necessary.

The units are $kg$ and $g/cm^{3}$ which are not compatible to be used in the formula.

First we must convert mass from $kg$ into $g.$

$1 \ kg = 1000 \ g$

$2.8 \ kg = 2.8 \times 1000=2800 \ g$

Substitute the values into the selected formula and carry out the resulting calculation.

\text{Volume}=\frac{\text{mass}}{\text{density}}=\frac{2800}{5.2}=538.46...

Write your final answer with the required units.

$500 \ cm^{3}$ (1sf)

Example 5: calculating mass with unit conversion

Liquid benzene has a density of $0.9 \ g/cm^{3}.$

Find the mass of $5 \ litres$ of liquid benzene.

Write down the values of the measures you know with the units.

\text{Density } = 0.9 \ g/cm^{3}

$\text{Mass } = \ ?$

$\text{Volume } = 5 \ litres$

Write down the formula you need to use from the density, mass, volume triangle.

We want to calculate mass.

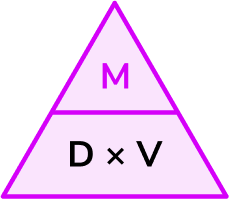
$\text{Mass}=\text{density}\times \text{volume}$

Check that the units are compatible with each other, converting them if necessary.

The units are $litres$ and $g/cm^{3}$ which are not compatible to be used in the formula.

First we must convert the volume from litres into $cm^{3}.$

$1 \ litre = 1000 \ cm^3$ so,

$5 \ litres = 5 \times 1000 = 5000 \ cm^3.$

We can now use the formula and calculate the mass in grams.

Substitute the values into the selected formula and carry out the resulting calculation.

\text{Mass}=\text{density}\times \text{volume}=0.9\times 5000=4500

Write your final answer with the required units.

4500 \ g

Example 6: calculating mass with unit conversion

Iron has a density of $7.8 \ g/cm^{3}.$

Find the mass of $620 \ cm^{3}$ of iron.

Give your answer in kilograms correct to $2$ significant figures.

Write down the values of the measures you know with the units.

\text{Density } = 7.8 \ g/cm^{3}

$\text{Mass } = \ ?$

$\text{Volume } = 620 \ cm^{3}$

Write down the formula you need to use from the density, mass, volume triangle.

We want to calculate mass.

$\text{Mass}=\text{density}\times \text{volume}$

Check that the units are compatible with each other, converting them if necessary.

The units are $cm^{3}$ and $g/cm^{3}$ which are compatible to calculate the mass in grams.

Substitute the values into the selected formula and carry out the resulting calculation.

\text{Mass}=\text{density}\times \text{volume}=7.8\times 620=4836

Write your final answer with the required units.

4836 \ g

$1 \ kg = 1000 \ g$

$4836 \div 1000 = 4.836$

$4.8 \ kg$

Common misconceptions

Thinking that density cannot be calculated because the volume is missing

When you are asked to calculate density you need to know what the mass and volume are. In some cases you will simply be given the volume but in other cases you may have to calculate the volume for yourself. Remember the volume of a cuboid is the product of its three dimensions.

For example,

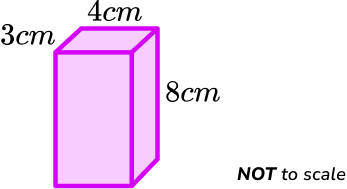
Formula for density misconception image 1

$\text{Volume}=3\times 4\times 8 = 96\ cm^3$

Step-by-step guide: How to calculate volume

Using incompatible units in a calculation

When using the formula for density you must ensure that the units of the measures are compatible. Density is usually measured in $g/cm^{3}$ or $kg/m^{3}.$ This table shows the compatible units.

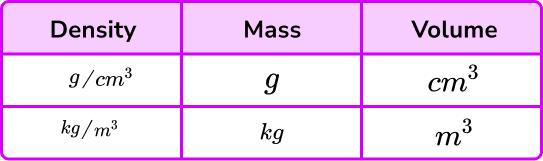
Formula for density misconception image 2

So, for example, if you are given a mass in grams but a volume in $m^{3}$ then these are not compatible and you must convert one of the measures.

Doing the correct calculation but writing your final answer incorrectly

Always think about the units of your final answer. Read the question carefully and check to see if any specific units are required. In some cases you may have to convert your answer into different units after a calculation.

Also check to see if the question requires your answer to be to a certain degree of accuracy such as one decimal place, or $2$ significant figures.

Practice formula for density questions

3 \ g/cm^3

\frac{1}{3} \ g/cm^3

270000 \ g/cm^3

0.3 \ kg/cm^3

\text{Density}=\frac{\text{mass}}{\text{volume}}=\frac{900}{300}=3 \ g/cm^3

0.726 \ g/cm^3

0.727 \ g/cm^3

1.38 \ g/cm^3

1.37 \ g/cm^3

$\text{Density}=\frac{\text{mass}}{\text{volume}}=\frac{950}{690}=1.3768…=1.38 \ g/cm^3$ (to 3 sf)

0.02 \ cm^3

50 \ cm^3

7200 \ cm^3

0.02 \ m^3

\text{Volume}=\frac{\text{mass}}{\text{density}}=\frac{600}{12}=50 \ cm^3

0.0452 \ cm^3

22.2 \ cm^3

22.1 \ cm^3

0.0453 \ cm^3

$\text{Volume}=\frac{\text{mass}}{\text{density}}=\frac{230}{10.4}=22.115…=22.1\ cm^3$ (to 3 sf)

0.6

0.6

3.84

3840

\text{Mass}=\text{density}\times \text{volume}=8\times 480=3840 \ g

But the question asks for the answer in $kg.$

3840 \ g= 3.84 \ kg

89.6 \ g

22.4 \ g

5.6 \ g

1.4 \ g

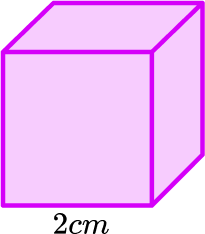
First we need the volume of the cube.

\text{Volume}=2\times 2\times 2=8\ cm^3

Then we can find the mass by multiplying the density by the volume.

\text{Mass}=\text{density}\times \text{volume}=11.2\times 8=89.6 \ g

Formula for density GCSE questions

1. A bouncy ball is made from a special type of material.

The ball has a mass of $450 \ g.$

The ball has a volume of $200 \ cm^3.$

Calculate the density of the material.

(2 marks)

Show answer

D=\frac{M}{V}=\frac{450}{200}=

(1)

2.25 \ g/cm^3

(1)

2. An iron bar has a mass of $25 \ kg.$

The density of iron is $7.8 \ g/cm^3.$

Work out the volume of the iron bar.

Give your answer in $cm^3$ correct to $3$ significant figures.

(3 marks)

Show answer

25\times 1000=25 \ 000 \ g

(1)

V=\frac{M}{D}=\frac{25 \ 000}{7.8}=3205.1…

(1)

$3210\ cm^3$ (to 3 sf)

(1)

3. The density of orange juice is $1.3 \ g/cm^3.$

The density of fizzy water is $0.98 \ g/cm^3.$

$30 \ cm^3$ of orange juice is mixed with $220 \ cm^3$ of fizzy water to make a fizzy orange drink.

Work out the density of the fizzy orange drink.

Give your answer correct to $3$ significant figures.

(4 marks)

Show answer

1.3\times 30=39

0.98\times 220=215.6

For mass of orange juice OR mass of fizzy water

(1)

39+215.6=254.6

(1)

Total volume $30 + 220 = 250$

D=\frac{M}{V}=\frac{254.6}{250}=1.0184

(1)

$1.02\ g/cm^3$ (to 3 sf)

(1)

Learning checklist

You have now learned how to:

Calculate the density of a substance

Calculate the volume of an object given its mass and density

Calculate the mass of an object given its volume and density

Change between related standard units

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.