Less than sign

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Place value Types of numbers Equivalent fractions Simplifying fractions

This topic is relevant for:

GCSE Maths Algebra Inequalities

Less Than Sign

Here we will learn about the less than sign including the symbol used to represent it, other comparison symbols and comparing numbers and expressions using the less than sign.

There are also inequality worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the less than sign?

The less than sign is a mathematical symbol used to compare numbers and expressions. Otherwise known as a comparison symbol.

The less than sign is

The wide end of the symbol always faces the bigger number or expression – the symbol looks open towards the bigger number and ‘points’ at the smaller value like an arrow.

For example,

This is read as $‘4$ is less than $9’.$

$11<18$ is read as $‘11$ is less than $18’.$

$1.3<1.7$ is read as $‘1.3$ is less than $1.7’.$

The less than sign is also used to represent inequalities in maths.

For example, $x<3$ is read as $‘x$ is less than $3’.$

Step-by-step guide: Inequalities

There are more comparison symbols (or inequality symbols) you need to know.

Equal to $=$ using the equal symbol denotes when two values are exactly equal.

For example, $3+4=7.$

Not equal to ≠ this not equal sign means two values are definitely not equal.

For example, $3+4$ ≠ $10.$

Identical to $\equiv$ symbol means two values are identical, even though they may be written in different forms.

For example, $4(x+2)\equiv 4x+8.$

Greater than $>$ denotes when one value is bigger than another.

For example, $8>7.$

Step-by-step guide: Greater than sign (coming soon)

Less than or equal to $\le$ denotes when we know a value is smaller or equal to.

Greater than or equal to $\ge$ denotes when we know a value is bigger or equal to.

What is the less than sign?

How to compare values using the less than sign

In order to compare values using the less than sign:

Compare the values given.
If less than, write the smaller value on the left hand side.
If less than, write the bigger value on the right hand side.
Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

Explain how to compare values using the less than sign

Inequalities on a number line worksheet (includes less than sign)

Get your free less than sign worksheet of 20+ inequalities on a number line questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Inequalities on a number line worksheet (includes less than sign)

Get your free less than sign worksheet of 20+ inequalities on a number line questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on inequalities

Less than sign is part of our series of lessons to support revision on inequalities. You may find it helpful to start with the main inequalities lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Less than sign examples

Example 1: comparing numbers

Write the correct sign, $>$ or $< ,$ in the box.

Compare the values given.

Both values are negative numbers.

$-28$ is further away from zero, so it is the smaller of the two values.

2If less than, write the smaller value on the left hand side.

$-28$ is the smaller number, and is written on the left side, so the less than symbol is pointing to it like an arrow.

3If less than, write the bigger value on the right hand side.

$-20$ is the greater number, and is written on the right side, so we draw the less than symbol with the open end next to the larger value.

4Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

Example 2: comparing numbers

Write the correct sign, $>$ or $< ,$ in the box.

Compare the values given.

Both values are positive.

$1.1$ is smaller than $1.8.$

If less than, write the smaller value on the left hand side.

$1.1$ is the smaller number, and is written on the left side, so the less than symbol is pointing to it like an arrow.

If less than, write the bigger value on the right hand side.

$1.8$ is the larger number, and is written on the right side, so we draw the less than symbol with the open end next to the larger value.

Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

Example 3: comparing fractions

Which is smaller, $\frac{3}{8}$ or $\frac{4}{9}?$

Write your answer using the correct comparison symbol.

Compare the values given.

To make it easier to compare the fractions we can write them with a common denominator.

$\frac{3}{8}=\frac{27}{72}$

$\frac{4}{9}=\frac{32}{72}$

$\frac{27}{72}$ is the smaller of the two values so $\frac{3}{8}$ is the smallest.

If less than, write the smaller value on the left hand side.

$\frac{3}{8}$ is the smallest value, so we write it on the left of the less than symbol.

$\frac{3}{8}<$

If less than, write the bigger value on the right hand side.

$\frac{4}{9}$ is the biggest value, so we write it on the right of the less than symbol.

$<\frac{4}{9}$

Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

\frac{3}{8}<\frac{4}{9}

Example 4: comparing fractions

Which is smaller, $3 \frac{4}{7}$ or $3 \frac{4}{9}?$

Write your answer using the correct comparison symbol.

Compare the values given.

To make it easier to compare the fractions we can write them as improper fractions with a common denominator.

$3 \frac{4}{7}=\frac{25}{7}=\frac{225}{63}$

$3 \frac{4}{9}=\frac{31}{9}=\frac{217}{63}$

$\frac{217}{63}$ is the smaller of the two values, so, $3 \frac{4}{9}$ is the smallest.

If less than, write the smaller value on the left hand side.

$3 \frac{4}{9}$ is the smallest value, so we write it on the left of the less than symbol.

$3 \frac{4}{9}<$

If less than, write the bigger value on the right hand side.

$3 \frac{4}{7}$ is the biggest value, so we write it on the right of the less than symbol.

$<3 \frac{4}{7}$

Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

3 \frac{4}{9}<3 \frac{4}{7}

Example 5: comparing expressions

Which is smaller, $18 \times 9$ or $186-35?$

Write your answer using the correct comparison symbol.

Compare the values given.

First we need to evaluate the expressions.

$18 \times 9=162$

$186-35=151$

So, $186-35$ is smaller than $18 \times 9.$

If less than, write the smaller value on the left hand side.

$186-35$ is the smallest value, so we write it on the left of the less than symbol.

$186-35<$

If less than, write the bigger value on the right hand side.

$18 \times 9$ is the biggest value, so we write it on the right of the less than symbol.

$<18 \times 9$

Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

186-35<18 \times 9

Example 6: comparing expressions

Which is smaller, $5(3x+8)$ or $3(5x+8)?$

Write your answer using the correct comparison symbol.

Compare the values given.

First we need to manipulate the expressions by expanding the brackets.

$5(3x+8)=15x+40$

$3(5x+8)=15x+24$

So, $3(5x+8)$ is smaller than $5(3x+8).$

If less than, write the smaller value on the left hand side.

$3(5x+8)$ is the smallest value, so we write it on the left of the less than symbol.

$3(5x+8)<$

If less than, write the bigger value on the right hand side.

$5(3x+8)$ is the biggest value, so we write it on the right of the less than symbol.

$<5(3x+8)$

Write the values with the correct symbol, or place the numbers on the correct sides of a given symbol.

3(5x+8)<5(3x+8)

We can only compare these two expressions as the coefficient of the term involving $x$ is the same.

Common misconceptions

Confusing the less than and greater than symbols

The biggest mistake is writing the symbols the wrong way round. Remember, the sign should point at the smallest number like an arrow.

For example, $15>8, \ ‘15$ is greater than $8’,$ or $8<15, ‘8$ is less than $15’.$

Equivalent fractions

When comparing fractions, we have to convert them into equivalent fractions with common denominators, so we can compare the numerators.

Practice less than sign questions

\frac{4}{11}>\frac{4}{9}

\frac{4}{11}<\frac{4}{9}

\frac{4}{9}>\frac{4}{11}

\frac{4}{9}<\frac{4}{11}

Convert the fractions to equivalents with a common denominator.

\frac{4}{11}=\frac{36}{99}

\frac{4}{9}=\frac{44}{99}

Comparing the numerators tells us that $\ \frac{36}{99}<\frac{44}{99} \$ so $\ \frac{4}{11}<\frac{4}{9}.$

-10>-18

-10<-18

-18>-10

-18<-10

Both values are negative. $-18$ is further from zero than $-10,$ so $-18$ is smaller than $-10.$

2 \frac{6}{7}<2 \frac{4}{5}

2 \frac{6}{7}>2 \frac{4}{5}

2 \frac{4}{5}>2 \frac{6}{7}

2 \frac{4}{5}<2 \frac{6}{7}

Convert the fractions to equivalents with a common denominator.

2 \frac{6}{7}=\frac{100}{35}

2 \frac{4}{5}=\frac{98}{35}

Comparing the numerators tells us that $\ \frac{98}{35}<\frac{100}{35} \$ so $\ 2 \frac{4}{5}<2 \frac{6}{7}$

7 \times 16>15 \times 8

7 \times 16<15 \times 8

15 \times 8<7 \times 16

15 \times 8>7 \times 16

Evaluating each expression gives,

7 \times 16=112

15 \times 8=120

So, $7 \times 16<15 \times 8.$

$20 \%$ of $3894<15 \%$ of $5686$

$20 \%$ of $3894>15 \%$ of $5686$

$15 \%$ of $5686<20 \%$ of $3894$

$15 \%$ of $5686>20 \%$ of $3894$

Evaluating each expression gives,

$20 \%$ of $3894=778.8$

$15 \%$ of $5686=852.9$

So, $20 \%$ of $3894<15 \%$ of $5686.$

6(2x+4)>3(4x+9)

6(2x+4)<3(4x+9)

3(4x+9)>6(2x+4)

3(4x+9)<6(2x+4)

Evaluating each expression gives,

6(2x+4)=12x+24

3(4x+9)=12x+27

So, $6(2x+4)<3(4x+9).$

Less than sign GCSE questions

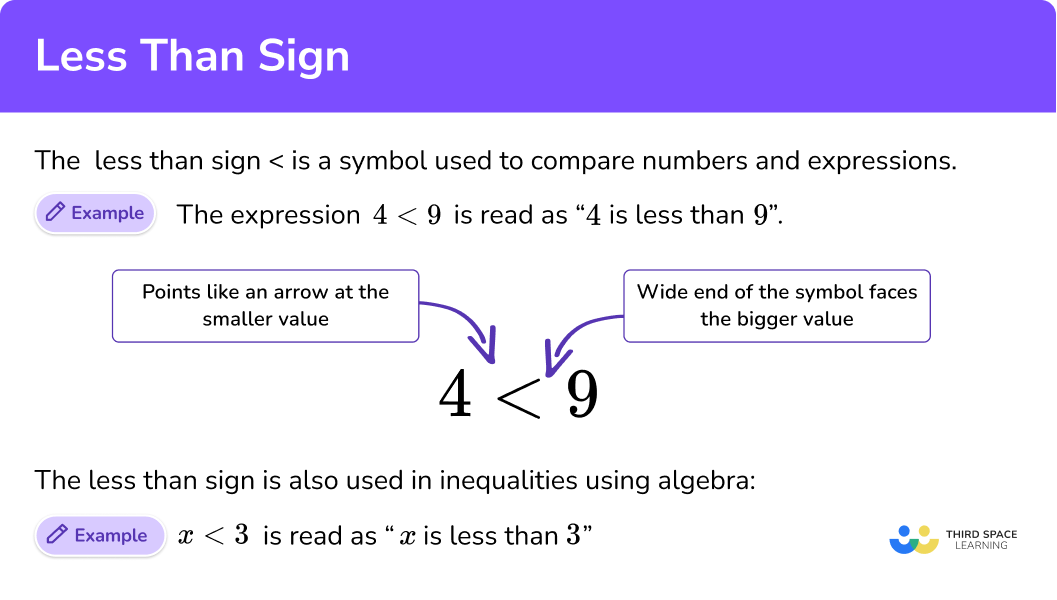
1. Write the correct sign $<, =,$ or ≠ in each box.

Less than sign GCSE question 1

(3 marks)

Show answer

100=10^2

(1)

$42+82$ ≠ $150-28$

(1)

25\times 6 <15\times 11

(1)

2. Here are four number cards.

Less than sign GCSE question 2

Arrange the cards to give a possible expression below.

Less than sign GCSE question 2-1

(1 mark)

Show answer

Any correct expression where the LHS is smaller than the RHS.

For example, $23<57 .$

(1)

3. Here are two fractions.

\frac{3}{4} \quad \quad \frac{7}{9}

Which fraction is smaller?

Complete the inequality expression below.

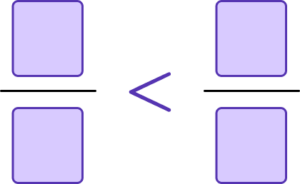
Less than sign GCSE question 3

(2 marks)

Show answer

$\frac{3}{4}=\frac{27}{36} \$ or $\ \frac{7}{9}=\frac{28}{36}$

(1)

\frac{3}{4}<\frac{7}{8}

(1)

Learning checklist

You have now learned how to:

Recognise the less than sign

Compare numbers and expressions

Write expressions using the less than sign

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction

What is the less than sign?

How to compare values using the less than sign

Less than sign worksheet

Less than sign examples

↓

Example 1: comparing numbers Example 2: comparing numbers Example 3: comparing fractions Example 4: comparing fractions Example 5: comparing expressions Example 6: comparing expressions

Common misconceptions

Practice less than sign questions

Less than sign GCSE questions

Learning checklist

Next lessons

Still stuck?