GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
This topic is relevant for:
Congruent Shapes
Here we will learn about congruent shapes, including what they are and how to recognise them.
There are also congruent shapes worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are congruent shapes?
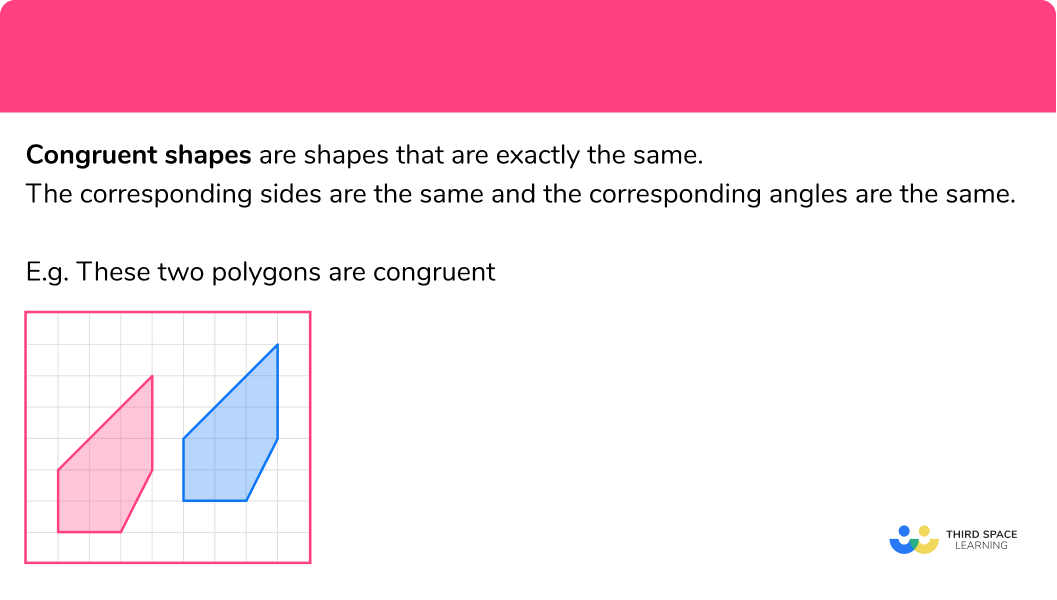
Congruent shapes are shapes that are exactly the same.
The corresponding sides are the same and the corresponding angles are the same.
To do this we need to check all the angles and all the sides of the shapes. If two shapes are congruent they will fit exactly on top of one another.
E.g.
These two polygons are congruent.
The red shape has been translated to give the blue shape.
E.g.
These two quadrilaterals are congruent.
The red shape has been reflected to give the blue shape.
E.g.
These two polygons are congruent.
The red shape has been rotated to give the blue shape.
E.g.
These two polygons are NOT congruent. They are similar.
The red shape has been enlarged by multiplying by a scale factor to give the blue shape.
If two shapes are the same but different sizes, one being an enlargement of the other, these are known as similar shapes.
What are congruent shapes?
Congruent triangles
There are four conditions to be able to prove if a pair of triangles are congruent.
Reasons for congruency:
SSS (three sides the same),
RHS (right-angled triangle, hypotenuse and a side the same),
ASA or AAS (two angles and one side the same),
SAS (side-angle-side, two sides and the included angle the same).
E.g.
These two triangles are congruent triangles.
They have two angles that are the same.
The side in between the angles is also equal.
The congruence condition would be angle-side-angle (which is abbreviated to ASA).
How to recognise congruent shapes
In order to recognise congruent shapes:
- Check the type of 2D shape.
- Check the corresponding angles and corresponding sides.
- State if the shapes are congruent or not.
Explain how to recognise congruent shapes
Congruent shapes worksheet
Get your free congruent shapes worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE Congruent shapes worksheet
Get your free congruent shapes worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on congruence and similarity
Congruent shapes is part of our series of lessons to support revision on congruence and similarity. You may find it helpful to start with the main congruence and similarity lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Congruent shapes examples
Example 1: congruent shapes
Are these 2D shapes congruent?
- Check the type of 2D shape.
Both shapes are rectangles.
2Check the corresponding angles and corresponding sides.
All the angles are 90^{\circ} .
The short sides on both rectangles are 1.
The long sides on both rectangles are 3.
3State if the shapes are congruent or not.
The shapes are the shape shape and the same size – they are congruent shapes.
Example 2: congruent shapes
Are these 2D shapes congruent?
Check the type of 2D shape.
Both shapes are rectangles.
Check the corresponding angles and corresponding sides.
All the angles are 90^{\circ} .
The short sides on both rectangles are 2.
The long sides on both rectangles are different.
State if the shapes are congruent or not.
The shapes are both rectangles but – they are NOT congruent shapes.
Example 3: congruent shapes
Are these 2D shapes congruent?
Check the type of 2D shape.
Both shapes are trapeziums.
Check the corresponding angles and corresponding sides.
The angles are 90^{\circ} , 45^{\circ} and 135 ^{\circ} .
They are in corresponding positions.
The lengths of the corresponding sides are different lengths.
The side lengths of the second shape are double the lengths of the first shape.
State if the shapes are congruent or not.
The shapes are the same shape, but different sizes. They are similar shapes but – they are NOT congruent shapes.
Example 4: congruent shapes
Are these 2D shapes congruent?
Check the type of 2D shape.
One shape looks like a capital letter “C” and the other shape looks like a capital letter “L”.
Check the corresponding angles and corresponding sides.
There are lots of right angles in both shapes.
There are lots of sides of length 1 and 3 .
But they are not in corresponding positions as the shapes are different shapes.
State if the shapes are congruent or not.
The shapes are different shapes. They are NOT congruent shapes.
Example 5: congruent shapes
Are these 2D shapes congruent?
Check the type of 2D shape.
It can be tricky to see if these shapes are the same type of 2D shape. They both have 6 sides so they are irregular hexagons.
Check the corresponding angles and corresponding sides.
The angles are 90^{\circ}, 225^{\circ} and 135^{\circ} .
They are in corresponding positions as you go the same direction around the shapes.
Looking at the side lengths – they are in corresponding positions as you go round the shapes in the same direction.
State if the shapes are congruent or not.
The shapes are the same shape and the same size. A rotation is involved. They are congruent shapes.
Example 6: congruent shapes
Are these 2D shapes congruent?
Check the type of 2D shape.
It can be tricky to see if these shapes are the same type of 2D shape. They both have 6 sides so they are irregular hexagons.
Check the corresponding angles and corresponding sides.
There are 4 right angles in both shapes.
The two other angles are equal and are in corresponding positions as you go round the shapes. But one in clockwise direction, one in an anticlockwise direction.
Looking at the side lengths there are lots of sides of length 1 and 3 and a diagonal.
They are in corresponding positions as you go round the shapes. But one in clockwise direction, one in an anticlockwise direction.
State if the shapes are congruent or not.
The shapes are the same shape and the same size. A rotation and a mirror image is involved. They are congruent shapes.
Common misconceptions
- Shapes can be congruent but in different orientations
The second shape may be in a different orientation to the first shape. The shapes can still be congruent. Perhaps use tracing paper to help you check.
- Shapes can be congruent but mirror images
The second shape may be a mirror image of the first shape. The shapes can still be congruent. Perhaps use tracing paper to help you check.
- Use the grid lines to help you compare shapes
Some shapes on a grid can be tricky. Use the straight lines on the grid to help you identify right angles and work out the side lengths. Be careful with the diagonals.
- In most diagrams the diagrams are NOT drawn to scale
Questions about congruent shapes are often on grids. But sometimes diagrams may have shapes which are NOT drawn to scale. So use the measurements given, rather than measuring for yourself.
Practice congruent shapes questions
1. Which shape is congruent to shape X?
A
B
C
D
The original shape is a rectangle with sides 1 and 4 . So has shape C.
2. Which shape is congruent to shape X?
A
B
C
D
Shape A is the same as the original shape, but has been rotated.
3. Which shape is congruent to shape X?
A
B
C
D
The original shape is a rectangle with sides 3 and 4. So has shape D.
4. Which shape is congruent to shape X?
A
B
C
D
Shape B is the same as the original shape, but is upside down.
5. Which shape is congruent to shape X?
A
B
C
D
Shape C is the same as the original shape, but is a reflection.
6. Which shape is congruent to shape X?
A
B
C
D
Shape C is the same as the original shape.
Congruent shapes GCSE questions
1. Which shape is congruent to shape X?
(1 mark)
Shape A
(1)
2. Which shape is congruent to shape A?
(1 mark)
Shape Y
(1)
3. Which shape is congruent to shape M?
(1 mark)
Shape D
(1)
Learning checklist
You have now learned how to:
- What congruent shapes are
- How to identify congruent shapes
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.
Find out more about our GCSE maths tuition programme.