GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Fractions Decimals Indices Coordinates maths Straight line graphsThis topic is relevant for:

Transformations
Here we will learn about transformations, including similar shapes and congruent shapes and triangles, reflections, translations, rotations and enlargements.
There are also transformations worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are transformations?
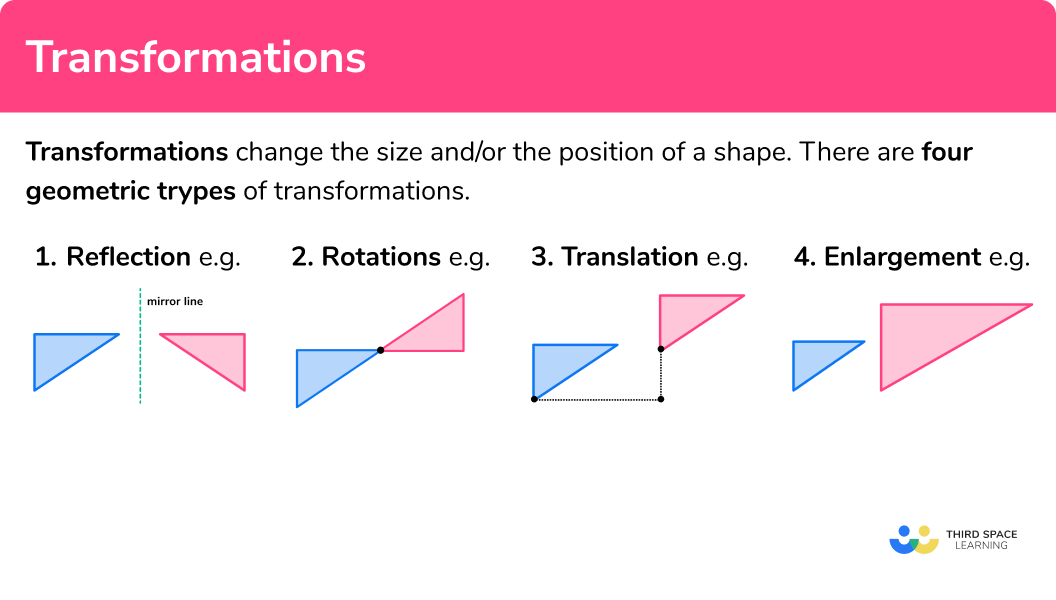
Transformations change the size and/or the position of a shape.
To do this we need a 2D shape (such as a polygon) and to follow the instructions given. These instructions are sometimes known as a mapping.
There are four geometric types of transformations:
Reflection
Reflections involve a mirror line, also known as a line of reflection.
E.g.
The shapes are congruent.
Step-by-step guide: Reflection
Rotations
Rotations involve a centre of rotation, an angle of rotation and a direction of rotation (clockwise or anticlockwise).
E.g.
The shapes are congruent.
Step-by-step guide: Rotations
Translation
Translations involve a move in a horizontal direction and a move in a vertical direction.
E.g.
The shapes are congruent.
Step-by-step guide: Translation
Enlargement
Enlargements make a shape bigger or smaller. They must have a scale factor and they may involve a centre of enlargement.
E.g.
The shapes are similar.
Questions can involve a single transformation or at Higher, GCSE questions can combine transformations.
When we combine transformations we need to do the first transformation on the original shape, then carry out a second transformation on the new shape.
Step by step guide: Enlargement
What are transformations?
What are scale factors?
Scale factors tell us how much bigger or smaller a shape will become when it is enlarged.
To enlarge a shape we multiply each side length of the shape by the scale factor.
They can be integers or fractions.
- If the scale factor is greater than
1 , the shape gets larger.
E.g.
The scale factor of enlargement from shape A to shape B is 2
- If the scale factor is between
0 and1 , the shape gets smaller.
E.g.
The scale factor of enlargement from shape A to shape B is \frac{1}{2} or 0.5
At GCSE Higher, there may be a negative scale factor of enlargement.
Step-by-step guide: Scale factor
What are invariant points?
Invariant points are points which have stayed in the same place after a transformation.
E.g.
Here is a reflection. The invariant point is labelled.
Similar and congruent shapes
For geometrical transformations we need to understand the terms similar and congruent.
- Similar shapes
Similar shapes are two or more shapes which are the same shape, but different sizes. One shape is an enlargement of the other.
E.g.
These two triangles are similar.
Step-by-step guide: Similar shapes
- Congruent shapes
Congruent shapes are shapes that are exactly the same.
E.g.
These two triangles are congruent.
Step-by-step guide: Congruent shapes
- Congruent triangles
Congruent triangles also have special conditions of congruence. These involve looking at their sides and angles.
The four conditions are known by abbreviations:
SSS (three sides the same),
RHS (right-angled triangle, hypotenuse and a side the same),
ASA or AAS (two angles and one side the same),
SAS (side-angle-side, two sides and the included angle the same).
Step-by-step guide: Congruent triangles
How to use transformations
- Use a pencil, additional construction lines and tracing paper to help.
- Remember:
Reflections have a mirror line.
Rotations have an angle of rotation, a direction and a centre of rotation.
Enlargements have a scale factor (and sometimes a centre of enlargement).
Translations have a distance across and a distance up or down. - Similar shapes are linked to enlargements.
- Congruent shapes are linked to reflection, rotations and translations.
Transformations worksheet

Get your free transformations worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Transformations worksheet

Get your free transformations worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREETransformations examples
Example 1: similar shapes
These shapes are similar. Find the value of x.
- Match up the corresponding sides and consider the ratio.
4:x=7:14
- Find a scale factor.
14\div 7 =2
- Use the scale factor to find the missing side.
x=4\times 2=8
The missing side is 8 cm .
Example 2: congruent shapes
Which shape is congruent to shape A?
- Look at the shapes and see if any are the same type of shape.
- Then look carefully and check the corresponding angles and sides. Congruent shapes can be rotated or reflected or both.
- Shape Y is congruent to shape A.
Example 3: congruent triangles
Are these triangles congruent?
- Check the corresponding sides and angles.
\begin{aligned} &\text{side} \ AC = \text{side} \ DE \\ &\text{angle} \ BAC = \text{angle} \ EDF\\ &\text{angle} \ BCA = \text{angle} \ FED \end{aligned}
- Triangle ABC is congruent to triangle DEF.
This is because they have two equal corresponding angles and the included side in both triangles is also equal. This is known as angle-side-angle (ASA).
Example 4: reflection
Reflect the shape in the mirror line.
- Consider each point (the vertices of the original shape) and reflect it in the mirror line. The new points will be the same distance from the mirror line as the original points.
- Then join up the new points.
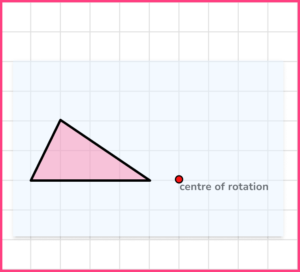
Example 5: rotations
Rotate the shape 90^{\circ} clockwise about the centre of rotation.
- Use tracing paper. Trace the original shape and check where the centre of rotation is.
- Put the tip of your pencil on the centre of rotation. Rotate the correct angle and in the right direction.
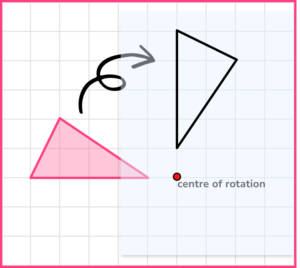
- Then draw your new shape onto the paper.
Example 6: translation
Translate the shape using the vector
\begin{pmatrix} 3\\ -1 \end{pmatrix}- Choose a point (vertex) of the original shape and move it using the column vector.
- The column vector gives instructions on how to move the original point.
\begin{pmatrix} 3\\ -1 \end{pmatrix} \text{is} \begin{pmatrix} 3 \ \text{right}\\ 1 \ \text{down}\\ \end{pmatrix}
- Repeat for the other points (vertices). Or you can just draw in the rest of the polygon. You may use tracing paper to check.
- Then join up the new points.
Example 7: enlargements – scale factor
Enlarge the shape by scale factor 3
- Choose a side to enlarge first. The left-side in the original shape is 1 , so the left-side in the new shape will be 9 . This can be drawn anywhere on the grid.
3\times3=9
- Enlarge the other sides using the same scale factor.
The lengths of the sides of the second shape are three times the lengths of the original shape.
Example 8: enlargements – centre of enlargement
Enlarge the shape by scale factor 2 , using the centre of enlargement.
- Draw ray lines through the centre of enlargement and each of the vertices of the original shape.
- Measure the distance from the centre of enlargement to a point (vertex) and then use the scale factor of 2 and mark the position of the new point.
- Repeat for the other points (vertices).
- Then join up the new points.
Example 9: combined transformations (Higher)
Reflect triangle A in the line x=1 to give triangle B. Reflect triangle B in the line y=0 to give triangle C.
Carry out the first transformation on the original shape (triangle A).
Then carry out the second transformation on the new shape (triangle B).The line y=0 is the x-axis.
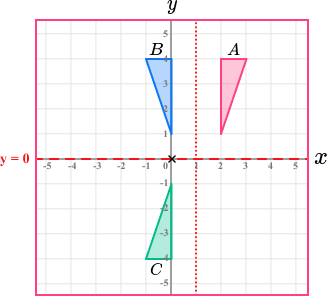
You may be asked to describe the single transformation that maps triangle A onto triangle C.
For this example the single transformation would be:Rotate triangle A 180° about (1,0) to give triangle C.
Common misconceptions
- Use the grid to help put the vertices of the shape in the correct position
Geometric transformations of shapes are often on grid paper. Use the lines and squares on the grid to help you be accurate about the position of the new shape.
- You can add extra details onto your diagram to help you
Try not to do transformation work in your head. Make use of your pencil and ruler to add marks to help you. You may also use tracing paper.
- Describe transformations fully
When you are asked to describe a transformation make sure you state which kind of transformation it is and all other details.
- Make sure you have the object and the image the right way around
The original shape is the object and the translated shape is the image. Make sure you know which shape is the original shape and start there when describing transformations such as translations.
Practice transformations questions
1. These two shapes are similar. Find the missing value of x .




Sides BC and CE are a pair of corresponding sides. Sides AC and CD are also a pair of corresponding sides.
\begin{aligned} BC:CE&=AC:CD\\\\ 4:12 \; &= \; 6:x \end{aligned}
The scale factor is
12\div4=3
x=6\times3=18
2. Reflect the shape in the mirror line.




Reflect each point in the mirror line. The new points will be the same distance from the mirror line as the original points.
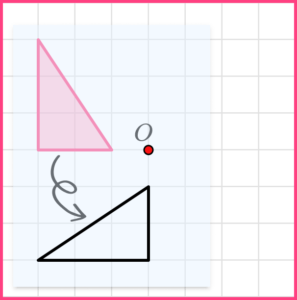
3. Rotate the shape 90^{\circ} anti-clockwise about the point O.




Use tracing paper to help with the rotation.
4. Translate the shape using the vector
\begin{pmatrix} -1\\ 4 \end{pmatrix}




The column vector gives the instructions on how to move each of the points.
\begin{pmatrix} -1\\ 4 \end{pmatrix} \; \text{is} \;\; \begin{aligned} &1 \ \text{left}\\ &4 \ \text{up}\\ \end{aligned}
5. Enlarge the shape using the scale factor \frac{1}{2}




The scale factor is \frac{1}{2} . The side lengths of the original shape need to be halved (or divided by 2 ). The height of the original shape is 4 , so the height of the new shape will be 2 .
4\times \frac{1}{2}=2
The base of the original shape is 2 , so the base of the new shape will be 1.
2\times \frac{1}{2}=1
6. Enlarge the shape by scale factor 3 , using the centre of enlargement O.




The distances between the points of the original shape and the centre of enlargement need to be multiplied by three.
\begin{aligned} &OP=2\\ &OP’=2\times 3=6 \end{aligned}
Transformations GCSE questions
1. Give a reason why the two triangles are congruent.
(1 mark)
Side-side-side (SSS)
(1)
2. Triangles ABC and DEF are similar.
Work out the value of x
(2 marks)
For the scale factor
(1)
x=3\times3=9For the correct value of x
(1)
3. (a) Translate shape A using the vector
\begin{pmatrix} 4\\ -1 \end{pmatrix}
(b) Describe the single transformation that maps shape A onto shape P.
(4 marks)
(a)
(2)
(b)
Reflection
(1)
In the line x=4
(1)
4 (higher). Triangle A is rotated 90^{\circ} clockwise about the point (0, 0) to give triangle B.
Triangle B is translated by the vector \begin{pmatrix} 3\\ 2 \end{pmatrix} to give triangle C.
Describe fully the single transformation that maps triangle A onto triangle C.
(3 marks)
Rotation
(1)
180^{\circ}(1)
About (1.5,2)
(1)
Learning checklist
You have now learned how to:
-
Recognise congruent shapes and triangles
-
Find missing lengths of similar shapes using a scale factor
-
Reflect shapes in a mirror line
-
Rotate shapes about a point
-
Translate shapes using a column vector
-
Enlarge shapes using a scale factor
-
Enlarge shapes with a centre of enlargement
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.