GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Probability tree diagram Fractions Decimals Independent events Mutually exclusive events Venn diagram Two-way tablesThis topic is relevant for:

Conditional Probability
Here we will learn about conditional probability, including the definition of conditional probability and how to calculate probabilities when there are conditional elements.
There are also conditional probability worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is conditional probability?
Conditional probability is the probability of an event occurring based on the occurrence of another event. Conditional probability is a fundamental aspect of probability theory.
Conditional probability questions often involve picking two objects from a set. This is because once you have picked the first object, the probabilities change for the second pick, based on the outcome of the first pick.
For example,
If we have a bag containing 3 strawberry sweets and 4 lemon sweets.

The probabilities of picking each type of sweet are
P(Strawberry) = \frac{3}{7}
P(Lemon) =\frac{4}{7}
If we picked out one strawberry sweet, there would be 2 strawberry sweets and 4 lemon sweets left.

The probabilities would now be
P(Strawberry) = \frac{2}{6}
P(Lemon) =\frac{4}{6}
If instead we picked out one lemon sweet, there would be 3 strawberry sweets and 3 lemon sweets left.
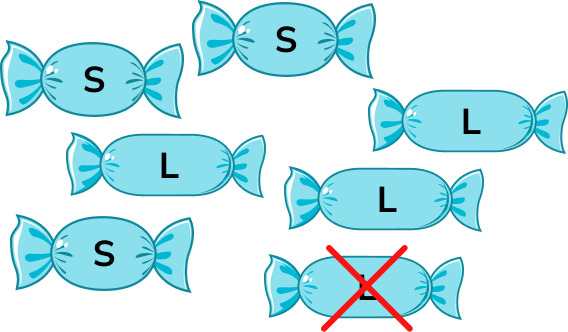
The probabilities would now be
P(Strawberry) = \frac{3}{6}
P(Lemon) =\frac{3}{6}
The probabilities are calculated based on what has already occurred.
What is conditional probability?

What is conditional probability?

How to calculate conditional probability
In order to calculate conditional probability:
- Identify the number of desired outcomes under the condition.
- Identify the total number of outcomes under the condition.
- Write the probability.
\text{Probability }=\frac{\text{number of desired outcomes}}{\text{total number of outcomes}}
Explain how to calculate conditional probability

Conditional probability worksheet
Get your free conditional probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONConditional probability worksheet
Get your free conditional probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONConditional probability examples
Example 1: using a Venn diagram
The diagram below shows the results when 25 students were asked whether they can speak French or Spanish.
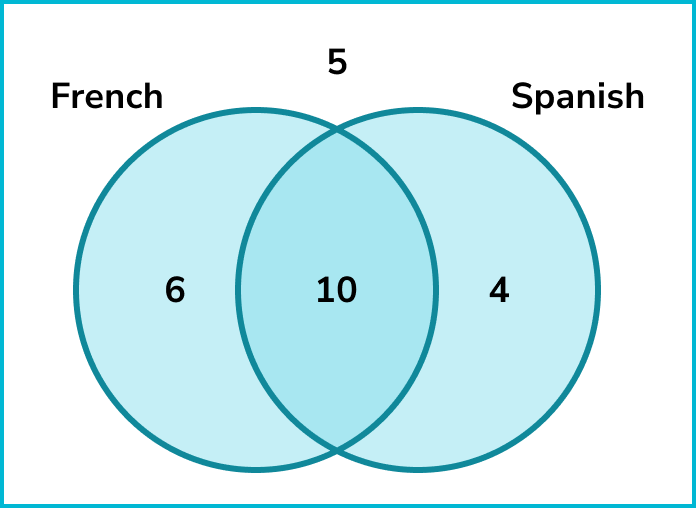
A student is chosen at random. Find the probability that the student can speak French given that they can speak Spanish.
- Identify the number of desired outcomes under the condition.
The desired outcome here is that the student speaks French.
The condition is that they speak Spanish.
We need to identify the number of students who speak French and Spanish.
There are 10 students who speak French and Spanish.
This will be the numerator of our fraction.
2Identify the total number of outcomes under the condition.
The condition is that they speak Spanish so we need to consider all the students who speak Spanish.
There are 10+4=14 students who speak Spanish.
This will be the denominator of our fraction.
3Write the probability.
\begin{aligned} \text{Probability }&=\frac{\text{number of desired outcomes}}{\text{total number of outcomes}}\\\\ \text{Probability }&=\frac{10}{14} \end{aligned}This probability can cancel to \frac{5}{7} .
Example 2: using a two-way table
The table below shows the hair and eye colour of a group of people.
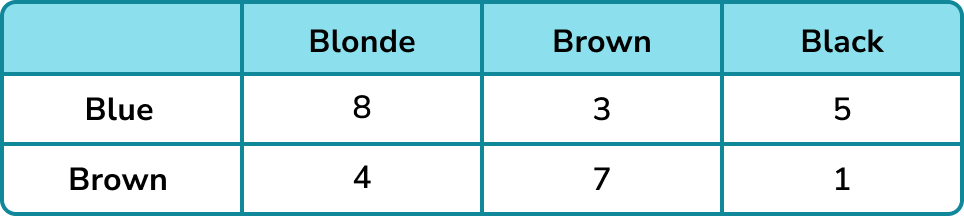
A person from the group is chosen at random. Find the probability that the person has blonde hair given that they have blue eyes.
Identify the number of desired outcomes under the condition.
The desired outcome here is that the person has blonde hair.
The condition is that they have blue eyes.
We need to identify the number of people who have blonde hair and blue eyes.
8 people have blonde hair and blue eyes.
Identify the total number of outcomes under the condition.
The condition is that the person has blue eyes.
There are 8+3+5=16 people with blue eyes.
Write the probability.
This probability can cancel to \frac{1}{2} .
Example 3: probability of one event given another event has occurred
A bag contains 6 blue balls and 10 yellow balls. One ball is picked and it is yellow, it is not put back into the bag. A second ball is then picked. Find the probability that the second ball is yellow given that the first ball was yellow.
Identify the number of desired outcomes under the condition.
The desired outcome here is picking a yellow ball.
The condition is that 1 yellow ball has already been picked.
Given that 1 yellow ball has already been picked and not replaced, there are now 9 yellow balls.
Identify the total number of outcomes under the condition.
The condition is that 1 yellow ball has already been picked.
Given that there were 16 balls to begin with and 1 has already been picked, there are 15 balls remaining.
Write the probability.
The probability the second ball is yellow is \frac{9}{15} .
This probability can cancel to \frac{3}{5} .
Example 4: probability of one event given another event
Lauren has a deck of cards. Lauren draws one card from the deck and does not replace it. The card she draws is an ace. Lauren then picks a second card. Find the probability that the second card is not an ace given the first card was an ace.
Identify the number of desired outcomes under the condition.
The desired outcome here is not picking an ace.
The condition is that one ace has already been picked.
There are 52 cards in a deck of cards, 4 of the cards are aces.
Given that there were originally 48 cards that were not aces and it is an ace that has been picked, so there are still 48 cards that are not aces.
Identify the total number of outcomes under the condition.
The condition is that one ace has been picked. If one card has been picked from the original 52 cards, there are a total of 51 cards left.
Write the probability.
The probability the next card is not an ace is \frac{48}{51} .
Example 5: probability of two events using a tree diagram
There are 12 socks in a drawer. 4 are white and 8 are black. William picks one sock and then picks a second sock without replacing the first. Find the probability that both socks are white.
We can draw a tree diagram to represent the possible outcomes,
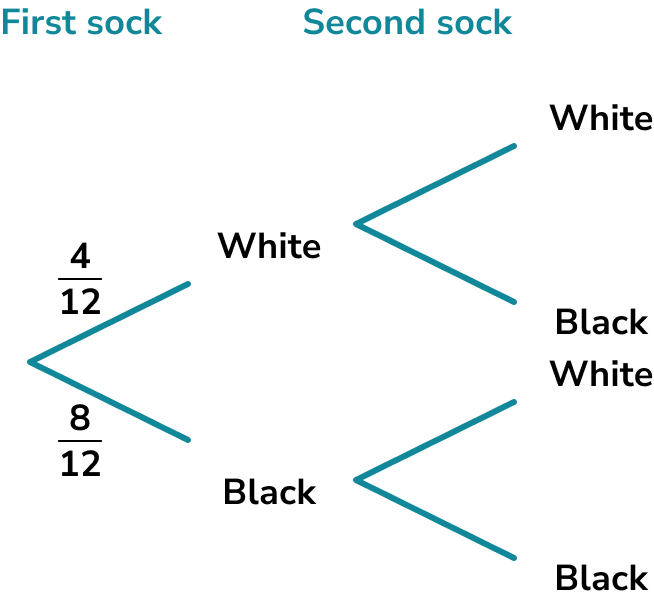
Since there are 12 socks to begin with, 4 of them white and 8 black, the probability of picking a white sock on the first pick is \frac{4}{12} and the probability of picking a black sock is \frac{8}{12}.
The probabilities for the second pick need to be calculated given the condition that the first pick has already occurred.
Let’s first assume that the first pick was a white sock.
Identify the number of desired outcomes under the condition.
If a white sock has already been picked there are now 3 white socks and 8 black socks.
Identify the total number of outcomes under the condition.
If a white sock has been picked, there are now 11 socks left altogether.
Write the probability.
Now let’s assume the first sock was black.
Identify the number of desired outcomes under the condition.
If a black sock has already been picked there are now 4 white socks and 7 black socks.
Identify the total number of outcomes under the condition.
If a black sock has been picked, there are now 11 socks left altogether.
Write the probability.
We can fill the rest of the tree diagram in.
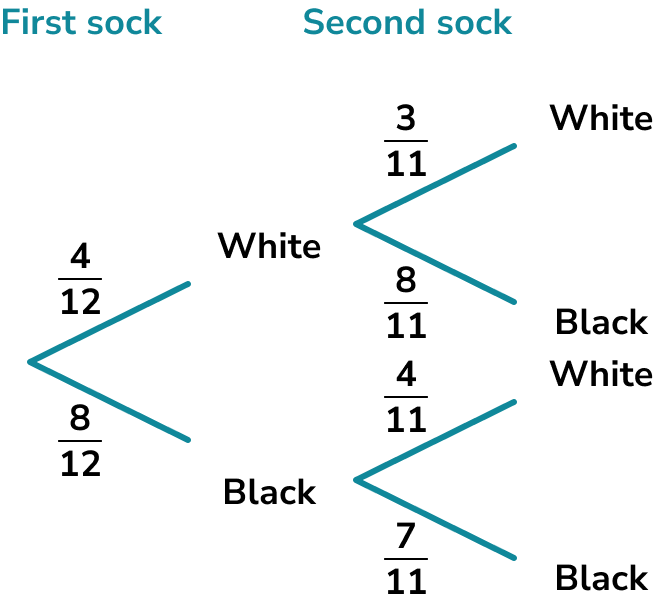
To find the joint probability that both socks are white we use
\text{P(A and B)}=\text{P(A)} \times \text{P(B)}
\begin{aligned}
\text{P(white and white)}&=\frac{4}{12} \times \frac{3}{11}\\\\
&=\frac{12}{132}\\\\
&=\frac{1}{11}
\end{aligned}
Example 6: probability of two events using a tree diagram
Karam has a box of chocolates containing 14 milk chocolates and 6 white chocolates. Karam eats 2 chocolates. Find the probability that Karam eats two chocolates of the same type.
We can represent this using a tree diagram.
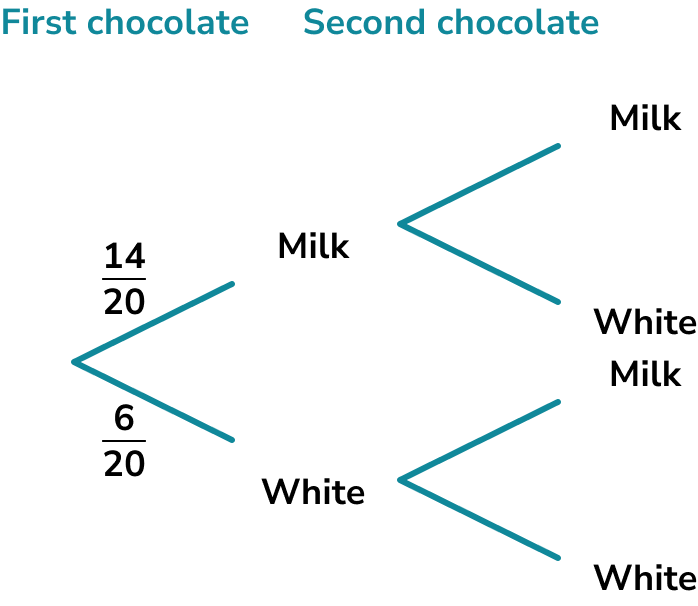
We need to work out the probabilities for the second chocolate.
If we assume the first chocolate was milk…
Identify the number of desired outcomes under the condition.
If the first chocolate was milk then there are 13 milk chocolates and 6 white chocolates left.
Identify the total number of outcomes under the condition.
If one chocolate has been picked, there are 19 chocolates left.
Write the probability.
If we assume the first chocolate was white…
Identify the number of desired outcomes under the condition.
If the first chocolate was milk then there are 14 milk chocolates and 5 white chocolates left.
Identify the total number of outcomes under the condition.
If one chocolate has been picked, there are 19 chocolates left.
Write the probability.
We can fill the rest of the tree diagram in.

To find the probability that he eats two of the same chocolates, we need the probability that he eats two milk chocolates or two white chocolates.
\begin{aligned} &\text{P(milk and milk)}=\frac{14}{20} \times \frac{13}{19} = \frac{182}{380}\\\\ &\text{P(white and white)}=\frac{6}{20} \times \frac{5}{19} = \frac{30}{380} \end{aligned}
The probability that Karam eats two of the same type of chocolate is
\frac{182}{380} + \frac{30}{380} = \frac{212}{380} = \frac{53}{95} .
Common misconceptions
- Not changing the probability for the second pick when picking two objects
For example, if you have a bag containing 3 blue balls and 7 yellow balls, the probability of picking a blue ball on the first pick is \frac{3}{10}.
If a blue ball has been picked on the first pick and not replced, then the probability of a blue ball on the second pick is \frac{2}{9} because there are 2 blue balls left and 9 balls altogether.
- Incorrect fraction work
Adding, subtracting, multiplying or dividing fractions incorrectly.
- Simplifying fractions
Usually when we have fractions in maths we simplify them. In probability questions it is usually better to leave fractions in their unsimplified form. This is because we often need to add fractions to solve probability problems.
Remember that fractions need a common denominator in order to add them. Check with the question if you are asked to give your final answer as a fraction in its simplified form or not.
Practice conditional probability questions
1. This Venn diagram shows the results when 30 people were asked whether they have a cat or a dog.
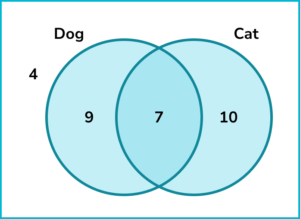
Find the probability that a person selected at random has a cat given that they have a dog.




The desired outcome is that the person has a cat and the condition is that they have a dog.
There are 7 people who have both a cat and a dog.
The condition is that the person has a dog. Altogether there are 16 people who have a dog.
The probability that the person has a cat given that they have a dog is \frac{7}{16}.
2. The two way table shows information about the gender and age of employees at a company.

A person from the company is chosen at random. Find the probability that the person is female given that they are 30 or over.




The desired outcome is that the person is female and the condition is that they are 30 or over.
There are 19 females who are 30 or over.
The condition is that the person is 30 or over. Altogether there are 36 people who are 30 or over.
The probability that the person is female given that they are 30 or over is \frac{19}{36} .
3. Lily has the following cards,
![]()
Lily picks two cards. The first card is an A. Find the probability that the second card is also an A.




If one A has already been picked, there will be one A left. There will be 7 cards left in total.
The probability that the second card is an A is \frac{1}{7} .
4. A football team contains 9 boys and 6 girls. The coach is choosing players at random for a match. The first player picked is a boy. Find the probability that the second player picked is a girl.




If one boy has been picked, there are 8 boys and 6 girls left, giving a total of 14 players. The probability the second player picked is a girl is \frac{6}{14}.
5. Ben and Jacob randomly pick a packet of crisps from a multipack containing 6 packs of ready salted and 6 packs of cheese and onion. What is the probability they both pick a packet of ready salted crisps? Give the answer in its simplest form.




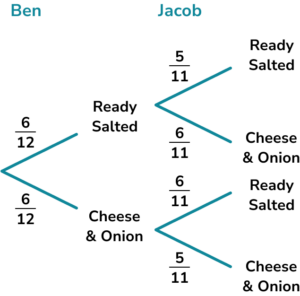
The probability they both pick ready salted is
\frac{6}{12} \times \frac{5}{11} = \frac{30}{132}=\frac{5}{22} .
6. Fred is a golf player. The probability that Fred gets a hole in one on a dry day is 0.2 and the probability that Fred gets a hole in one on a rainy day is 0.1. Fred is going to play golf tomorrow.
The probability that it will be raining is 0.7. Find the probability that Fred will get a hole in one.





We need to consider the probability of Fred getting a hole in one on a dry day or a rainy day.
The probability that Fred gets a hole in one and it is a dry day is
0.3 \times 0.2 = 0.06 .
The probability that Fred gets a hole in one and it is a wet day is
0.7 \times 0.1=0.07 .
The total probability that Fred gets a hole in one is
0.06+0.07=0.13.
Conditional probability GCSE questions
1. Vicky has a box of chocolates containing 5 white chocolates and 11 milk chocolates. Vicky eats one milk chocolate.
Find the probability that the next chocolate she picks is also a milk chocolate.
(2 marks)
10 or 15
(1)
Probability =\frac{10}{15} or \frac{2}{3}
(1)
2. (a) This two way table shows information about a group of people’s favourite preferred cereal. Complete the two way table.

(b) Find the probability that a person picked at random prefers muesli given that they are female.
(4 marks)
(a)

For 2 correct values.
(1)
For all 4 values correct.
(1)
(b)
12 or 45 seen
(1)
\frac{12}{45} or \frac{4}{15}
(1)
3. There are 8 counters in a bag. Three of the counters are red and the rest are blue. A counter is chosen at random. It is not replaced. A second counter is chosen at random.
Calculate the probability that both counters are blue.
(3 marks)
P(first counter is blue) =\frac{5}{7}
(1)
P(second counter is also blue) =\frac{4}{6}
(1)
P(both counters are blue) =\frac{5}{8} \times \frac{4}{7}
(1)
\frac{20}{56} or \frac{5}{14}
(1)
4. Tom designs a game. Players must roll a fair dice. If they get a multiple of 3 , they pick a ball from bag A. If they get any other number, they pick a ball from bag B.
Bag A contains 4 red balls and 6 blue balls.
Bag B contains 2 red balls and 8 blue balls.
A player wins if they pick a red ball. Find the probability a player wins the game.
(4 marks)
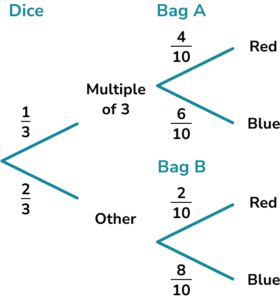
\begin{aligned} &\text{P(multiple of 3)}=\frac{1}{3}\\ &\text{P(not multiple of 3)}=\frac{2}{3} \end{aligned}
(1)
\text{P(red A)}=\frac{1}{3} \times \frac{4}{10} = \frac{4}{30}(1)
\text{P(red B)}=\frac{2}{3} \times \frac{2}{10}=\frac{4}{30}(1)
\text{P(red total)}=\frac{4}{30}+\frac{4}{30}=\frac{8}{30}=\frac{4}{15}(1)
Learning checklist
You have now learned how to:
-
Calculate probabilities of given events based on conditions
-
Apply conditional probability of events to solve problems
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.