GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Area of a triangle Inverse functions Rounding to decimal places Rounding to significant figures Pythagorean theorem

This topic is relevant for:

GCSE Maths Geometry and Measure Trigonometry Trigonometry Formula

Area Of A Triangle Trig

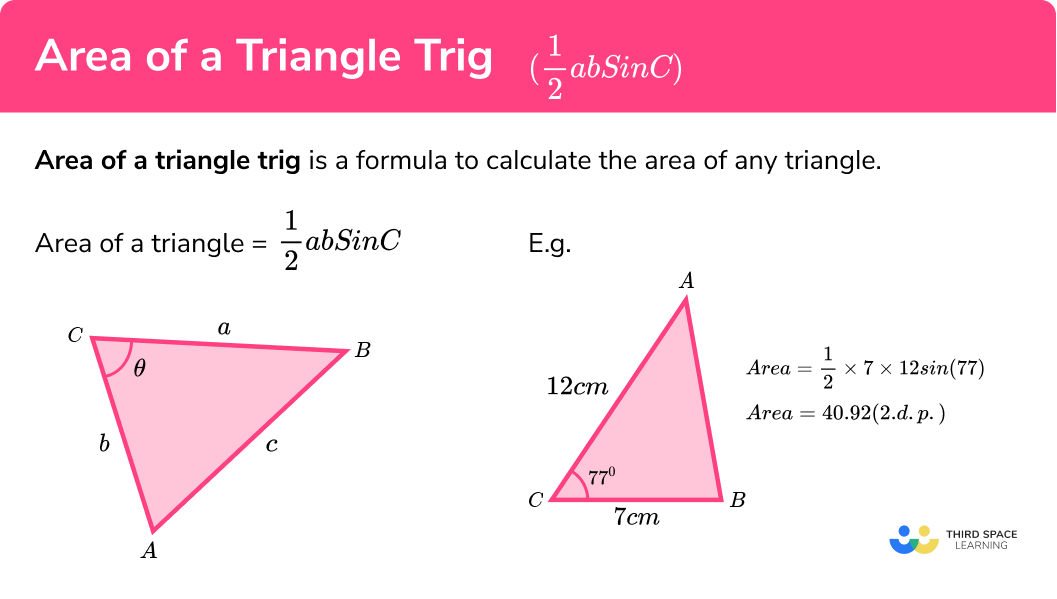
Area Of A Triangle Trig (½abSinC)

Here is everything you need to know about finding the area of a triangle using trigonometry for GCSE maths (Edexcel, AQA and OCR). You’ll learn how to generate the area of a triangle formula, use the formula to find the area of a triangle and apply this formula to other polygons.

Look out for the Area of a Triangle worksheets and exam questions at the end.

What is the area of a triangle ‘trig’ (½abSinC)

Area of a triangle trig is a formula to calculate the area of any triangle:

\[\text{Area of triangle }=\frac{1}{2}ab\sin C \]

Previously, we have calculated the area of a triangle using another formula:

\[\text{Area of a triangle }=\frac{\text{base} \times \text{height}}{2}\]

To use this we need to know the vertical height (perpendicular height to the base) of the triangle and the base of the triangle.

We can adapt this formula using the trigonometric ratio $\sin(\theta)=\frac{O}{H}$ to work out the area of a triangle when we do not know its vertical height. The formula we get is:

\[\text{Area of triangle }=\frac{1}{2}ab\sin C\]

The triangle should be labelled as follows, with the lower case letter for each side opposite the corresponding upper case letter for the angle.

We need to know:

The length of at least 2 sides of the triangle.
The included angle between these two sides.

For example, triangle ABC has been labelled where C is the included angle between the two edges of the triangle a and b.

What is the area of a triangle trig (½abSinC)?

Which area of a triangle formula should I use?

If we know or can work out the vertical height of a triangle, it can be easier to use the following formula:

\[\text{Area of a triangle }=\frac{\text{base} \times \text{height}}{2}\]

E.g.

However, if the vertical height is not labelled and we know two sides and the angle in between, we would need to use the following:

\[\text{Area of triangle }=\frac{1}{2}ab\sin C\]

Once we know which formula to use we need to substitute the correct values into it and then solve the equation to calculate the area. The area is always written with square units.

Remember: other polygons can be split into triangles to find the interior angles,

so:

\[\text{Area of triangle }=\frac{1}{2}ab\sin C\]

can be applied to find the area of a rectangle, the area of an equilateral triangle, the area of a pentagon, the area of a parallelogram, etc.

Step by step guide: Angles in polygons.

How to find the area of a triangle using Area = ½abSinC

In order to find the area of a triangle using

\[\text{Area of triangle }=\frac{1}{2}ab\sin C\]

Label the angle we are going to use angle C and its opposite side c. Label the other two angles B and A and their corresponding side b and a.
Substitute the given values into the formula $\text{Area }=\frac{1}{2}absinC.$
Solve the equation.

How to find the area of a triangle using Area = ½abSinC.

Area of a triangle trig ½abSinC worksheet

Get your free area of a triangle trig ½abSinC worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area of a triangle trig ½abSinC worksheet

Get your free area of a triangle trig ½abSinC worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area of a triangle (½abSinC) examples

Example 1: with two sides and the angle in between

Calculate the area of the triangle ABC. Write your answer to 2 decimal places.

Label the angle we are going to use angle C and its opposite side c.
Label the other two angles A and B and their corresponding side a and b.

2Substitute the given values into the formula

\[A=\frac{1}{2}ab\sin(C)\]

\[A=\frac{1}{2}\times12\times7\times\sin(77)\]

3Solve the equation.

\[\begin{aligned} A&=\frac{81.84708544}{2}\\ A&=40.92\mathrm{cm}^{2} \end{aligned}\]

Example 2: with two sides and the angle in between

Calculate the area of the triangle. Write your answer to 2 decimal places.

Label the angle we are going to use angle C and its opposite side c. Label the other two angles A and B and their corresponding side a and b.

Here, we label each side a, b, and c and each vertex A, B and C.

Substitute the given values into the formula.

\[A=\frac{1}{2}ab\sin(C)\]

\[A=\frac{1}{2}\times18.2\times10\times\sin(65)\]

Solve the equation.

\[\begin{aligned} A&=\frac{164.9480172}{2}\\ A&=82.47\mathrm{m}^{2} \end{aligned}\]

Example 3: with three sides and one angle

Calculate the area of the scalene triangle PQR. Write your answer to 3 significant figures.

Label the angle we are going to use angle C and its opposite side c. Label the other two angles A and B and their corresponding side a and b.

Here, we label each side and each angle.

Substitute the given values into the formula.

\[A=\frac{1}{2}ab\sin(C)\]

\[A=\frac{1}{2}\times5.5\times3.6\times\sin(24)\]

Solve the equation.

\[\begin{aligned} A&=\frac{8.053385533}{2}\\ A&=4.03\mathrm{cm}^{2} \end{aligned}\]

Example 4: area of an isosceles triangle with a known angle

Triangle XYZ is an isosceles triangle. Find the area of the triangle to 2 decimal places.

Label the angle we are going to use angle C and its opposite side c. Label the other two angles A and B and their corresponding side a and b.

Here, we label each side and each angle.

Substitute the given values into the formula.

\[A=\frac{1}{2}ab\sin(C)\]

As the triangle XYZ is isosceles, b=c.

\[A=\frac{1}{2}\times 9.7\times11.8\times\sin(45)\]

Solve the equation.

\[\begin{aligned} A=\frac{80.93544217}{2}\\ A=40.47\mathrm{km}^{2} \end{aligned}\]

Example 5: with two sides and two angles

Calculate the area of the triangle ABC. Write your answer to 2 decimal places.

Label the angle we are going to use angle C and its opposite side c. Label the other two angles A and B and their corresponding side a and b.

Here, we label 22^o as C as this angle is between two known sides.

Substitute the given values into the formula.

\[A=\frac{1}{2}ab\sin(C)\]

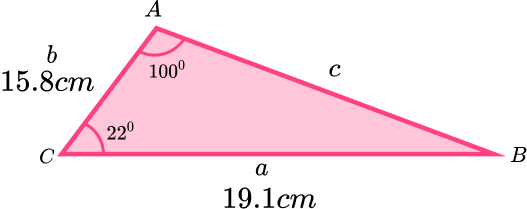
Here, we need to be careful to use the correct angle of C=22^o.

\[A=\frac{1}{2}\times19.1\times15.8\times\sin(22)\]

Solve the equation.

\[\begin{aligned} A&=\frac{113.0487778}{2}\\ A&=56.52\mathrm{cm}^{2} \end{aligned}\]

Example 6: with two sides and two angles

Calculate the area of the triangle ABC. Write your answer to 4 significant figures.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

Here, we have to think carefully because a, b, and C do not correspond to a, b and C in

\[A=\frac{1}{2}ab\sin(C)\]

As the known sides b and c have the included angle at A with all three values known, we can adjust the sine rule to make

\[A=\frac{1}{2}bc\sin(A)\]

Substitute the given values into the formula.

\[A=\frac{1}{2}bc\sin(A)\]

\[A=\frac{1}{2}\times 165\times131\times\sin(9)\]

Solve the equation.

\[\begin{aligned} A&=\frac{3381.330962}{2}\\ A&=1691\mathrm{mm}^{2} \end{aligned}\]

Example 7: finding a length given the area

The area of this triangle is 30cm². Find the length labelled x.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

Substitute the given values into the formula.

\[A=\frac{1}{2}ab\sin(C)\]

This time we know the area, one side and the angle.

Therefore:

\[30=\frac{1}{2}\times x\times12\times\sin(38)\]

Solve the equation.

\[\begin{aligned} 30&=6 \times x \times 0.616\\ 30&=3.694x\\ 8.12&=x \end{aligned}\]

x is 8.12cm.

Example 8: finding an angle given the area

The area of this triangle is 42cm². Find the angle labelled x.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

Substitute the given values into the formula.

\[A=\frac{1}{2}ab\sin(C)\]

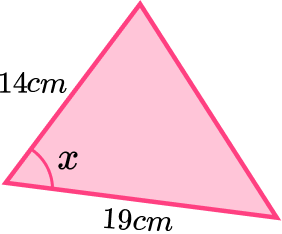
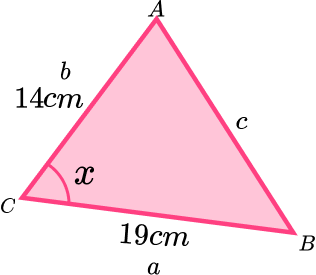
This time we know the area and two sides.

Therefore:

\[42=\frac{1}{2}\times 19\times14 \times\sin(x)\]

Solve the equation.

\[\begin{aligned} 42&=133\sin(x)\\ \frac{42}{133}&=\sin(x)\\ 0.316&=\sin(x)\\ x&=sin^{-1}(0.316)\\ x&=18.4^{\circ} \end{aligned}\]

Where does the formula Area = ½abSinC come from?

We derive the formula for the area of any triangle by taking the triangle ABC, with vertical height, h:

By applying the usual formula for the area of a triangle $(\frac{\text{base}\times\text{height}}{2})$ we have $A=\frac{1}{2}(a\times{h})$ .

We can also state, using trigonometry, that $\sin(C)=\frac{h}{b}$ which we can rearrange to make h the subject $h=b\sin(C)$ .

Substituting $h=b\sin(C)$ into $A=\frac{1}{2}(a\times{h})$ , we obtain: $A=\frac{1}{2}ab\sin(C)$ .

It is important to notice that C is the included angle between the sides of a and b.

Common misconceptions

Incorrectly labelling the triangle so the substitution is incorrect

Not using the included angle between $a$ and $b$ .

The triangle is assumed to contain a right angle and so the area is calculated by halving the base times the height.

Using inverse sine instead of sine of the angle to find the area.

Area of a triangle trig is part of our series of lessons to support revision on trigonometry. You may find it helpful to start with the main trigonometry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice area of a triangle trig questions

189\mathrm{m}^{2}

163.7\mathrm{m}^{2}

94.5\mathrm{m}^{2}

378\mathrm{m}^{2}

Label the triangle:

\begin{aligned} \text{Area }&=\frac{1}{2}ab \sin(C)\\ \text{Area }&=\frac{1}{2} \times 21 \times 18 \times \sin(30)\\ \text{Area }&=94.5 \mathrm{m}^{2} \end{aligned}

32.85\mathrm{m}^{2}

7.95\mathrm{m}^{2}

31.87\mathrm{m}^{2}

18.60\mathrm{m}^{2}

Label the triangle:

\begin{aligned} \text{Area }&=\frac{1}{2}ab \sin(C)\\ \text{Area }&=\frac{1}{2} \times 7.3 \times 9 \times \sin(76)\\ \text{Area }&=31.87 \mathrm{m}^{2} \end{aligned}

74.31\mathrm{m}^{2}

42.90\mathrm{m}^{2}

85.81\mathrm{m}^{2}

81.72\mathrm{m}^{2}

Label the triangle:

\begin{aligned} \text{Area }&=\frac{1}{2}ab \sin(C)\\ \text{Area }&=\frac{1}{2} \times 13.1 \times 13.1 \times \sin(60)\\ \text{Area }&=74.31 \mathrm{m}^{2} \end{aligned}

125.41\mathrm{mm}^{2}

250.81\mathrm{mm}^{2}

376.22\mathrm{mm}^{2}

225.83\mathrm{mm}^{2}

We need to look at the two triangles individually. The triangles are congruent (exactly the same) since all three of their lengths are equal (SSS). Therefore we can calculate the area of one triangle and then double it.

Label one triangle:

\begin{aligned} \text{Area }&=\frac{1}{2}ab \sin(C)\\ \text{Area }&=\frac{1}{2} \times 15 \times 22.5 \times \sin(48)\\ \text{Area }&=125.406 \mathrm{mm}^{2}\\ \text{Total area }&=2\times125.406=250.81\mathrm{mm}^{2} \end{aligned}

18.7\mathrm{cm}^{2}

12.4\mathrm{cm}^{2}

10.6\mathrm{cm}^{2}

17.3\mathrm{cm}^{2}

First, calculate angle PQR: $180-28.3-28.3=123.4{\circ}$ .

Then label the triangle:

\begin{aligned} \text{Area }&=\frac{1}{2}ab \sin(C)\\ \text{Area }&=\frac{1}{2} \times 6.7 \times 6.7 \times \sin(123.4)\\ \text{Area }&=18.7 \mathrm{cm}^{2} \end{aligned}

\theta=60^{\circ}

\theta=14.5^{\circ}

\theta=0.5^{\circ}

\theta=30^{\circ}

\begin{aligned} \text{Area } &=\frac{1}{2}ab \sin(C)\\ 210&=\frac{1}{2} \times 24 \times 35 \times \sin(\theta)\\ 210&=420 \sin(\theta)\\ 0.5&= \sin(\theta)\\ \sin^{-1}(0.5)&=\theta\\ 30^{\circ}&=\theta \end{aligned}

Area of a triangle trig GCSE questions

1. In triangle {katex]ABC[/katex], $AB$ =8m, $AC$ =18m and angle $BAC$ = $31^{\circ}$ . Calculate the area of triangle $ABC$ .

(2 marks)

Show answer

A=\frac{1}{2}\times 8 \times 18 \times \sin(31)

(1)

A=37.1\mathrm{m}^{2}

(1)

2. Quadrilateral $ABCD$ is made from two triangles.

a) Work out the length $AC$ .
b) Calculate the total area of the quadrilateral.

(5 marks)

Show answer

\begin{aligned} 11^{2}&=7^{2}+b^{2}\\ b^{2}&=11^{2}-7^{2} \end{aligned}

(1)

\begin{aligned} b^{2}&=72\\ b&=\sqrt{72}\\ b&=8.49\mathrm{cm} \end{aligned}

(1)

\text{Area ABC: } \frac{1}{2} \times 7 \times 8.49 =29.72 \mathrm{cm}^{2}

(1)

\begin{array}{l} \text{Area ACD: } \frac{1}{2} \times 8 \times 8.49 \times \sin(64)\\ \text{Area ACD }=30.52 \mathrm{cm}^2 \end{array}

(1)

\text{Total area: }29.72+30.52=60.2\mathrm{cm}^{2}

(1)

3. The area of triangle PQR is $55cm^2$ . Work out the value of $x$ . Give your answer to 2dp.

(4 marks)

Show answer

\frac{1}{2} \times x \times 2x \times \sin(29) = 55

(1)

\begin{aligned} x^{2} \times \sin(29) &=55\\ 0.485x^{2}&=55 \end{aligned}

(1)

x^{2}=113.447

(1)

x=10.65cm

(1)

Learning checklist

You have now learned how to:

Know and apply

\text{Area}=\frac{1}{2}ab\sin C

to calculate the area, sides or angles of any triangle

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.