3D trigonometry

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

In order to access this I need to be confident with:

Sine rule Cosine rule Tangent of a circle Plans and elevations Exact trig values Surds Decimal places How to find the midpoint

This topic is relevant for:

GCSE Maths Geometry and Measure Trigonometry

3D Trigonometry

Here we will learn about 3D trigonometry including how to combine your knowledge of Pythagoras’ Theorem, Trigonometric Ratios, The Sine Rule and The Cosine Rule and apply it to find missing angles and sides of triangles in 3-dimensional shapes.

There are also 3D trigonometry worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is 3D trigonometry?

3D trigonometry is an application of the trigonometric skills developed for 2 dimensional triangles.

To find missing sides or angles in 3 dimensional shapes, we need to be very clear which rules and formulae we need to use in order to find different angles and side lengths.

The flowchart below can help determine which function you need to use:

You may need to carry out this process several times in a question to fully answer what is being asked. You must be able to justify which rule or formulae you need to use.

Top Tip: Look out for common angles or common sides.

What is 3D trigonometry?

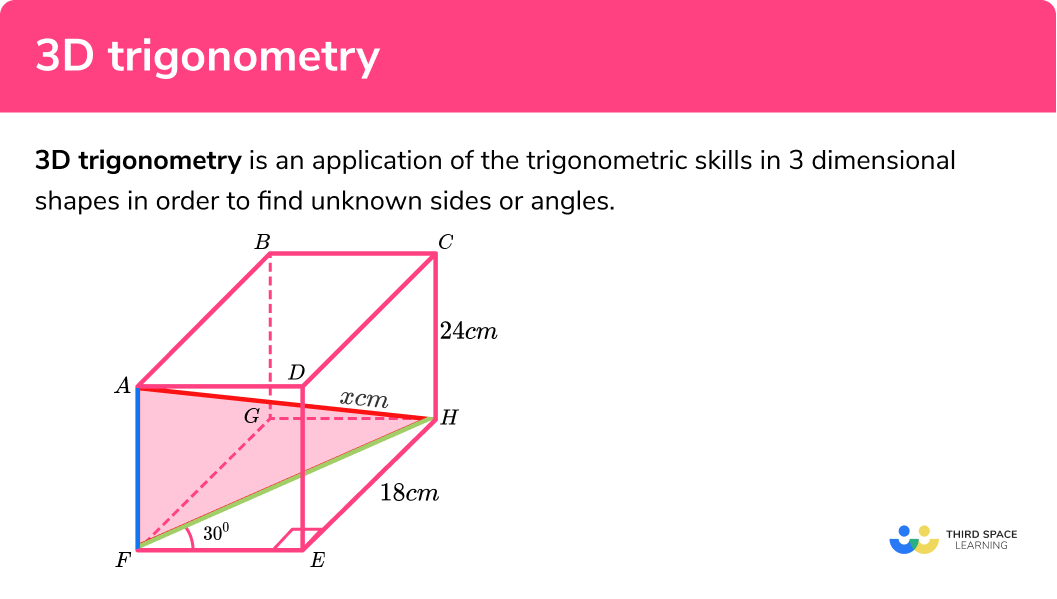
How to use 3D trigonometry to find a missing angle or side length

In order to find a missing angle or side within a 3-dimensional shape:

Calculate the necessary missing angle or side of a triangle.
Sketch and label the second triangle using information from Step 1.
Calculate the missing angle or side of the final triangle.

Explain how to use 3D Trigonometry to find a missing angle or side length.

3D trigonometry worksheet

Get your free 3D trigonometry worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

3D trigonometry worksheet

Get your free 3D trigonometry worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

3D trigonometry examples

Example 1: missing side using trigonometry and Pythagoras’ theorem

The diagram shows a cuboid.

Calculate the length of the line $AH$ . Write your answer in the form $a\sqrt{b}\mathrm{cm}$ where $a$ and $b$ are integers.

Calculate the necessary missing angle or side of a triangle.

The line FH is shared between the two triangles EFH and AFH. We can find the length of FH by using simple trigonometric ratios.

Here we need to find the value of FH (the hypotenuse):

\[\begin{aligned} H&=\frac{O}{\sin(\theta)}\\\\ H&=\frac{18}{\sin(30)}\\\\ H&=36\mathrm{cm}\\\\ FH&=36\mathrm{cm} \end{aligned} \]

2Sketch and label the second triangle using information from step 1.

3Calculate the missing angle or side of the final triangle.

AFH is a right angle triangle, so we can use Pythagoras’ Theorem to find the value of x:

\[\begin{aligned} c^{2}&=a^{2}+b^{2}\\\\ x^{2}&=24^{2}+36^{2}\\\\ x^{2}&=1872\\\\ x&=12\sqrt{13}\mathrm{cm} \end{aligned} \]

Example 2: finding length using trigonometric ratios

ABCDEF is an isosceles triangular prism. DF is 7cm, Angle DFE is 75^o and angle ECF is 40^o. Find the length of the line CE.

Calculate the necessary missing angle or side of a triangle.

The triangle DEF is isosceles. We can split it in two and find the length of EF by using trigonometric ratios.

We need to find the value of x (the hypotenuse):

\[\begin{aligned} &H=\frac{A}{\cos(\theta)}\\\\ &x=\frac{3.5}{ \cos(75)}\\\\ &x=13.52296157\mathrm{cm} \end{aligned} \]

Sketch and label the second triangle using information from step 1.

You must remember not to round your solution too early. Here we will continue to use the full decimal given for x = 13.52296157 .

Calculate the missing angle or side of the final triangle.

Here we have a right angle triangle so we can use another trigonometric ratio to find the length CE:

\[\begin{aligned} H&=\frac{O}{\sin(\theta)}\\\\ CE&=\frac{13.52296157}{\sin(40)}\\\\ CE&=21.03799352…\\\\ CD&=21.34\mathrm{cm}\qquad(3.d.p) \end{aligned} \]

Example 3: missing angle including midpoint

ABCDEFGH is a cuboid with the following information:

The front face of the cuboid is a square.
The midpoint M lies half-way between E and F .
The line AC is at 30^o from the line AB .
BCM is a triangle.
AC = 52cm
$CE=26\sqrt{3}$

Using the diagram below, calculate the size of angle BMC, to 2 decimal places.

Calculate the necessary missing angle or side of a triangle.

The line BC is shared between the two triangles ABC and BCM. We can find the length of BC by using trigonometric ratios.

Here we need to find the value of BC (the opposite side to the angle $\theta$ ):

\[\begin{aligned} O&=H\sin(\theta)\\\\ O&=52\sin(30)\\\\ O&=26\mathrm{cm}\\\\ BC&=26\mathrm{cm} \end{aligned} \]

Sketch and label the second triangle using information from step 1.

As M is a midpoint along EF, this gives us an isosceles triangle BCM. As we know $CE=26\sqrt(3)$ this is the vertical height of the triangle.

Calculate the missing angle or side of the final triangle.

As we can split an isosceles triangle into two right-angle triangles, and we can use trigonometric ratios to find the angle $\frac{\theta}{2}$ then multiply by $2$ to find $\theta$ :

\[\begin{aligned} \frac{\theta}{2}&=\tan^{-1}(\frac{O}{A})\\\\ \frac{\theta}{2}&=\tan^{-1}(\frac{13}{26\sqrt(3)})\\\\ \frac{\theta}{2}&=16.10211375…\\\\ \theta&=32.20\mathrm{cm}\qquad(2dp) \end{aligned} \]

Example 4: missing angle using the cosine rule

ABCDEFGH is a cuboid. BH, FH and BF are straight lines that connect to make a triangle BFH. Using the information in the diagram, calculate the size of angle HFB.

Calculate the necessary missing angle or side of a triangle.

Each side of the triangle BFH is the hypotenuse of one of the three faces of the cuboid. As we have all three dimensions of the cuboid, we can calculate each value (x, y, z) as follows:

Here we need to find the value of x (the hypotenuse):

\[\begin{aligned} x^{2}&=5^{2}+12^{2}\\\\ x&=\sqrt{25+144}\\\\ x&=13\mathrm{cm}\\\\ BF&=13\mathrm{cm}\\\\ \end{aligned} \]

Here we need to find the value of y (the hypotenuse):

\[\begin{aligned} y^{2}&=9^{2}+5^{2}\\\\ y&=\sqrt{81+25}\\\\ y&=\sqrt{106}\mathrm{cm}\\\\ BH&=\sqrt{106}\mathrm{cm} \end{aligned}\]

Here we need to find the value of z (the hypotenuse):

\[\begin{aligned} z^{2}&=9^{2}+12^{2}\\\\ z&=\sqrt{81+144}\\\\ z&=\sqrt{225}\mathrm{cm}\\\\ FH&=15\mathrm{cm} \end{aligned} \]

Sketch and label the second triangle using information from step 1.

Keeping $BH=\sqrt{106}$ , we now have the triangle BFH:

Calculate the missing angle or side of the final triangle.

As we know the three side lengths of the triangle, we can use the cosine rule to find the missing angle $\theta.$

\[\begin{aligned} \cos(A)&=\frac{b^{2}+c^{2}-a^{2}}{2bc}\\\\ \cos(A)&=\frac{288}{390}\\\\ A&=cos^{-1}(\frac{288}{390})\\\\ A&=42.39947336…\\\\ A&=42.4^{\circ} (1.d.p) \end{aligned} \]

Example 5: missing angle using the sine rule

The diagram shows a triangular prism.

Angle DEC = 50º
Angle EBC = 55º
AE = AD

The angle ϴ lies between the two lines CE and BE. Calculate the size of angle ϴ. Show all your working.

Calculate the necessary missing angle or side of a triangle.

The line CE is shared between the two triangles CDE and BCE. We can find the length of CE by using trigonometric ratios.

Here we need to find the value of CE (the hypotenuse):

\begin{aligned} \\H&=\frac{O}{\sin(\theta)}\\ \\H&=\frac{25}{\sin(50)}\\ \\CE&=32.63518223…\mathrm{cm}\\ \end{aligned}

Sketch and label the second triangle using information from step 1.

Calculate the missing angle or side of the final triangle.

We know two sides and one of the two opposite angles so we need to use the sine rule to find the value for ϴ.

\begin{aligned} \\\sin(\theta)&=\frac{\sin(55)}{32.63518223…}\times{23}\\ \\\theta&=\sin^{-1}(0.5773063219)\\ \\\theta&=35.26130584…\\ \\\theta&=35.26^{\circ}\quad(2dp)\\ \end{aligned}

Example 6: missing side using the sine rule

The diagram shows a cylinder:

A, B and D are points on the circumference of the circles.
C is the centre of the circle.
ABC is a triangle
AD is the diameter of the cylinder.

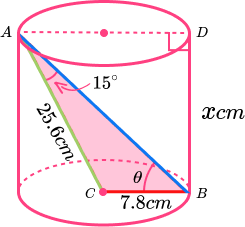
By calculating the size of angle $\theta$ , work out the height of the cylinder.

Calculate the necessary missing angle or side of a triangle.

As we know two sides and one of the two opposite angles, we can use the sine rule to find the missing angle $\theta$ .

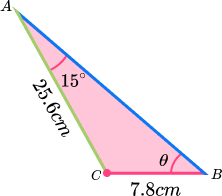
3D Trigonometry (Example 6 Step 1) Image 20

Here we need to find the value of $\theta$ :

$\begin{aligned} \sin(\theta)&=\cfrac{\sin(15)}{7.8}\times{25.6} \\\\ \theta&=\sin^{-1}(0.8494573788) \\\\ \theta&=58.15269987… \\\\ \theta&=58.2^{\circ} \; (2dp) \end{aligned}$

Sketch and label the second triangle using information from step 1.

As AD is the diameter of the circle, we can label AD as 2 × BC = 15.6cm.

As the angle CBD is 90º, we can calculate the angle ABD to equal $90-58.1526…=31.8473…^{\circ}.$

We now have enough information on the second triangle to calculate the height of the cylinder. Remember not to round too early.

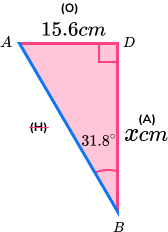
3D Trigonometry (Example 6 Step 2) Image 21

Calculate the missing angle or side of the final triangle

To find the value of x, we use a simple trigonometric ratio.

\begin{aligned} A&=\cfrac{O}{\tan(\theta)} \\\\ x&=\cfrac{15.6}{\tan(31.8473….)} \\\\ x&=25.1139…. \\\\ x&=25.11 \; cm \; (2dp) \end{aligned}

Common misconceptions

Using Pythagoras’ Theorem instead of trigonometry

Using two sides of a non right-angle triangle to find the third side instead of using the cosine rule.

Incorrect trigonometric ratio used

Incorrect labelling of any triangle can lead to the wrong trig function being used.

Confusing the Sine Rule with the Cosine Rule

Misunderstanding when to use the sine rule or cosine rule to find a missing side or angle.

Using the inverse trig function instead and inducing a mathematical error

If the inverse trig function is used instead of the standard trig function, the calculator may return a maths error as the solution does not exist.

3D trigonometry is part of our series of lessons to support revision on trigonometry. You may find it helpful to start with the main trigonometry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice 3D trigonometry questions

9.04cm

10.33cm

7.53cm

15.82cm

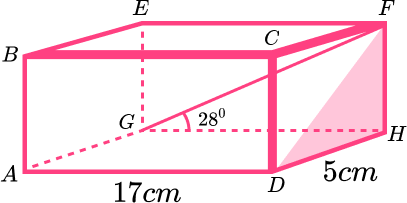
Let’s first look at triangle $FGH:$

We want to know the length of $FH$ which is the opposite.

$\begin{aligned} O&=A \tan(\theta)\\\\ O&=17 \tan(28)\\\\ O&=9.039060338 \mathrm{cm} \end{aligned}$

Now that we know the length of $FH$ , we can consider the triangle $DFH:$

Since we know two sides and we want to calculate the third side, we can use Pythagoras Theorem:

 $\begin{aligned} c^{2}&=a^{2}+b^{2}\\\\ c^{2}&=5^{2}+9.039060338^{2}\\\\ c^{2}&=106.7046118\\\\ c&=\sqrt{106.7046118}\\\\ c&=10.33 \mathrm{cm} \end{aligned}$

43.7^{\circ}

21.0^{\circ}

35.8^{\circ}

39.3^{\circ}

First we need to look at the triangle $DEF:$

We need to find the length of $DE$ , which is the opposite.

\begin{aligned} O&=H \sin(\theta)\\\\ O&=9sin(62)\\\\ O&=7.946528336 \mathrm{cm} \end{aligned}

Now that we know the length of $DE,$ we can consider the triangle $ADE$ :

We want to find the angle $DAE.$ We know $O$ and $A$ .

\begin{aligned} \tan(\theta)&=\frac{O}{A}\\\\ \tan(\theta)&=\frac{7.946528336}{11}\\\\ \theta&=\tan^{-1}(\frac{7.946528336}{11})\\\\ \theta&=35.8^{\circ} \end{aligned}

282.84m

400m

565.69m

70.71m

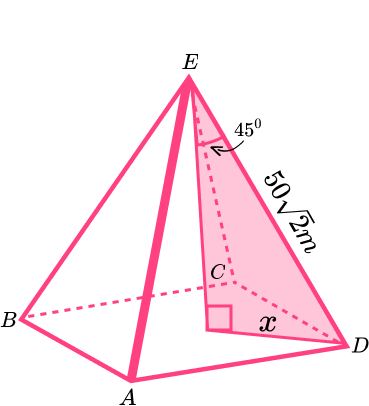
First we need to work out the value of $x:$

\begin{aligned} O&= H \sin(\theta)\\\\ O&=50 \sqrt{2} \sin(45)\\\\ O &=50 \mathrm{m} \end{aligned}

Now we can look at the base:

The length of the sides can be found using Pythagoras Theorem:

\begin{aligned} &c^2=a^2+b^2\\\\ &c^2=50^2+50^2\\\\ &c^2=5000\\\\ &c=70.71m \end{aligned}

Each side is $70.71m$ therefore the perimeter is:

4 \times 70.71=282.84 \mathrm{m}

76.60^{\circ}

38.22^{\circ}

32.01^{\circ}

51.78^{\circ}

$AB, AC$ and $BC$ can all be worked out using Pythagoras Theorem:

\begin{aligned} &AB^2=500^2+800^2\\ &AB^2=890000\\ &AB=943.3981132\\\\ &AC^2=750^2+800^2\\ &AC^2=1202500\\ &AC=1096.58561\\\\ &BC^2=500^2+750^2\\ &BC^2=812500\\ &BC=901.388189\\ \end{aligned}

We can then apply the cosine rule:

The length of the sides can be found using Pythagoras Theorem:

\begin{aligned} \cos(A)&=\frac{b^{2}+c^{2}-a^{2}}{2bc}\\\\ \cos(A)&=\frac{1096.58561^{2}+943.3981132^{2}-901.388189^{2}}{2 \times 1096.58562 \times 943.3981132}\\\\ \cos(A)&=0.6186459892\\\\ A&=\cos^{-1}(0.6186459892)\\\\ A&=51.87^{\circ} \end{aligned}

38.7^{\circ}

38.5^{\circ}

51.3^{\circ}

36.4^{\circ}

First we need to calculate the length of $EH.$ We can do this using Pythagoras Theorem:

\begin{aligned} a^{2}&=c^{2}-b^{2}\\\\ a^{2}&=20^{2}-12^{2}\\\\ a^{2}&=256\\\\ a&=16 \mathrm{cm} \end{aligned}

We can now look at the triangle $EGH:$

We can calculate angle $GEH$ using the sine rule:

\begin{aligned} \frac{\sin(A)}{a} &= \frac{sin(B)}{b}\\\\ \frac{\sin(\theta)}{10} &= \frac{sin(85)}{16}\\\\ \sin(\theta)&= \frac{sin(85)}{16} \times 10\\\\ \sin(\theta)&= 0.6226216863\\\\ \theta&= \sin^{-1}(0.6226216863)\\\\ \theta&=38.5^{\circ} \end{aligned}

36.5^{\circ}

51.3^{\circ}

9.2^{\circ}

18.0^{\circ}

We need to calculate the length $XZ$ using the triangle $CXZ:$

\begin{aligned} O&=A \tan(\theta)\\\\ O&=5 \tan(76)\\\\ O&=20.05390467 \mathrm{cm} \end{aligned}

We can now look at triangle $XYZ:$

Using the cosine rule:

\begin{aligned} \cos(A) &= \frac{b^{2}+c^{2}-a^{2}}{2bc}\\\\ \cos(\theta)&= \frac{32^{2}+32^{2}-20.05390467^{2}}{2 \times 32 \times 32}\\\\ \cos(\theta)&=0.8036332556\\\\ \theta&= \cos^{-1}(0.8036332556)\\\\ \theta&=36.5^{\circ} \end{aligned}

3D Trigonometry GCSE questions

1. $ABCDEFGH$ is a cuboid.

Calculate the angle between the diagonal DF and the base $AEHD$ .

Give your answer to $3$ sf.

3D Trigonometry (Exam question 1)

(4 marks)

Show answer

Triangle $ADE:$

DE^{2}=8^{2}+12^{2}

(1)

\begin{aligned} DE&=\sqrt{208}\\\\ DE&=14.4222\mathrm{cm} \end{aligned}

(1)

Triangle $DEF:$

\tan(\theta)=\frac{8}{14.4222}

(1)

\begin{aligned} \theta&=\tan^{-1}(\frac{8}{14.4222})\\\\ \theta&=29.0^{\circ} \end{aligned}

(1)

2. $ABCDEF$ is a triangular prism.

The cross-section of the prism is an isosceles triangle.

$M$ is the midpoint of $AC$ .

Calculate the length of $EM$ .

3D Trigonometry (Exam question 2)

(4 marks)

Show answer

\tan(70)=\frac{x}{4.5}

(1)

\begin{aligned} 4.5\tan(70)&=x\\\\ 12.364&=x \end{aligned}

(1)

\begin{aligned} EM^{2}&=16^{2}+12.364^{2}\\\\ EM^{2}&=408.868 \end{aligned}

(1)

\begin{aligned} EM&=\sqrt{408.868}\\\\ EM&=20.2\mathrm{cm} \end{aligned}

(1)

3. Find the size of the angle $AFH$ .

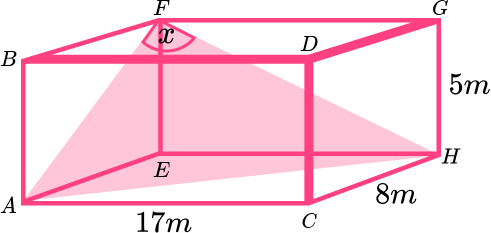
(6 marks)

Show answer

\begin{aligned} AF^{2}&=8^{2}+5^{2}\\\\ AF&=9.434 \end{aligned}

(1)

\begin{aligned} FH^{2}&=17^{2}+5^{2}\\\\ FH&=17.720 \end{aligned}

(1)

\begin{aligned} AH^{2}&=17^{2}+8^{2}\\\\ AH&=18.788 \end{aligned}

(1)

\cos(x)=\frac{9.434^{2}+17.720^{2}-18.788^{2}}{2\times9.434\times17.720}

(1)

\cos(x)=0.1096

(1)

\begin{aligned} x&=\cos^{-1}(0.1496)\\\\ x&=81.4^{\circ} \end{aligned}

(1)

Learning checklist

You have now learned how to:

Apply Pythagoras’ Theorem and trigonometric ratios to find angles and lengths in right-angled triangles (and, where possible, general triangles) in 2 (and 3) dimensional figures

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction

What is 3D trigonometry?

How to use 3D trigonometry to find a missing angle or side length

3D trigonometry worksheet

3D trigonometry examples

↓

Example 1: missing side using trigonometry and Pythagoras’ Theorem Example 2: finding length using trigonometric ratios Example 3: missing angle including midpoint Example 4: missing angle using the cosine rule Example 5: missing angle using the sine rule Example 6: missing side using the sine rule

Common misconceptions

Related lessons

Practice 3D trigonometry questions

3D trigonometry GCSE questions

Learning checklist

Next lessons

Still stuck?