The 18 Maths Formulas Students Need To Learn For GCSE And How To Teach Them 

GCSE maths formulas are a fundamental part of GCSE maths preparation. This blog looks at strategies to help students in the run-up to their exams with a couple of common related problems: remembering formulae and concepts, and working out which formula or concept to apply to a question.

What is a formula in maths?

A formula in maths is a rule, fact or key principle expressed in mathematical symbols, rather than words. Equations, inequalities and equalities can all be formulae. However, at GCSE, a formula usually includes an equals sign (equality), and two or more variables.  

In GCSE mathematics, the general definition of a formula is that there is some kind of application of the algebraic rule, either to solving a mathematical problem, such as trigonometric formulae, or modelling a real-world concept, such as the SUVAT formulae. Most formulae in GCSE maths come up in Geometry and Measures.

What formulas are needed for GCSE maths exams?

The formulas listed by the three main exam boards (Edexcel, AQA and OCR) as necessary for students to memorise are given below.

Formulae with a star (*) are required for Higher maths only.

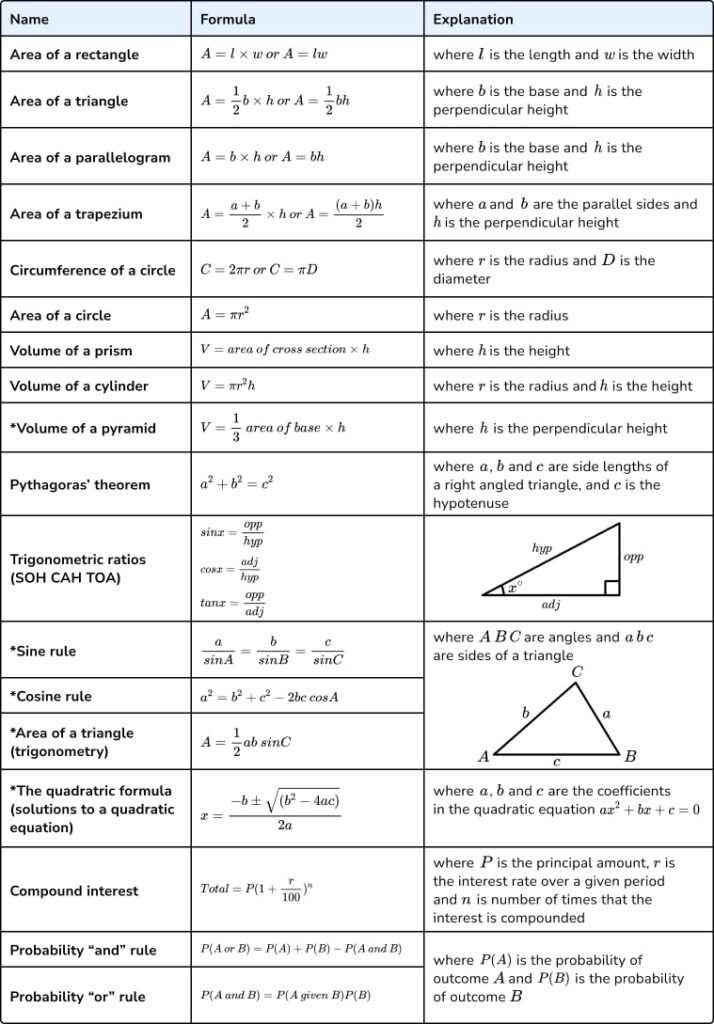
Students are given these formulae in the exam when required, but they still need to be familiar with their use:

There are also a few other concepts that students need to memorise, such as the general form for the equation of a circle centred at (0,0), the equation of a straight line, and so on.

See also: Maths curriculum

What formulas are needed for GCSE Science?

Students also encounter formulae in other subjects such as physics and chemistry – this is a great opportunity for cross-curricular work with your science department.

Some formulae that students may come across in Science include:

This is a broad, general list – I recommend liaising with your Science department to work out which are applicable for the specific board and qualifications studied by your students.

Make sure students aren’t trying to ‘memorise’ methods!

The first thing to establish with students is exactly what they’re trying to memorise; some students try to patch over a shaky understanding of key concepts by attempting to memorise every step of a process. 

While memorisation of key formulae is necessary for success at GCSE, students should be discouraged from trying to memorise methods without underlying conceptual understanding. We also need to be aware of the capacity of working memory and the speed at which we move away from modelling and diagrams.

Memorisation vs conceptual understanding

Consider students working on a standard procedural fraction addition, such as \frac{1}{4}+\frac{2}{5}. Student A has attempted to memorise and follow a series of steps, whereas Student B is happier working with bar modelling. If Student A is unable to recall a step in a learned procedure (for example, getting a common denominator) they will be unable to progress with the question, whereas Student B may be more likely to recall that equal sized pieces are important, as this is the case with most bar modelling of fraction arithmetic. 

The key point here is that, for some students on some topics, a diagrammatic approach may well be an appropriate end point, and forcing more formal written methods can sometimes result in them jumbling up which method applies to which case.

This is not just the case for simpler or lower-level concepts – I’ve taught completing the square using a pictorial method (algebra tiles) before moving to the more formal ‘half b’ method; some students felt more comfortable remaining with the algebra tile method and applied this successfully in their exams.

If a student is complaining of being unable to ‘remember the method’, or is mixing up methods, such as applying KFC (keep, flip, change) to a fraction addition, it is likely that there are misconceptions around the underlying principles, so these should be addressed if possible. This is more achievable the earlier the problem is highlighted, which is why early intervention is important.

At Third Space Learning, our online one-to-one GCSE revision programme is personalised to each individual student and aims to fill the gaps in conceptual understanding. We work to go beyond memorisation, familiarising students with formulas and illustrating their meanings to teach to understanding. 

See also:

• How to revise for GCSE
• How to revise for maths

In the rest of the article, we’ll look at some strategies to help students memorise the formulae they need at GCSE, and how to help students correctly identify what formula to apply when faced with GCSE maths questions.

Strategies for helping students to learn formulas

1. Teach the conceptual ideas behind a mathematical formula

It’s really helpful if students have some conceptual understanding behind a new mathematical formula – otherwise it becomes a bit like a sleight-of-hand magic trick where you’re saying to students, “Yes, this always works, just trust me.” 

In many cases, a pure mathematical derivation will be beyond the capabilities of most students – for example, some of the volume and surface area formulae derivations involve calculus. However, visual demonstrations are incredibly useful to show students that these formulae aren’t just random numbers.

In some cases, such as the quadratic formula, students can attempt their own derivations with some scaffolding. However, this kind of more rigorous work is best left until after students are more familiar with the ideas involved – so I probably wouldn’t show students how to derive the quadratic formula by completing the square until they were really confident with both of those concepts individually.

2. Embed recall of formulae into classroom teaching

My rule of thumb here is to only ever tell them a formula once – so, for example, as soon as they have the quadratic formula written down in their exercise books and we’ve done a worked example to go with it, I then expect them to refer back to that each time they identify a question that requires the quadratic formula. A few other strategies you can use include:

• When working on an example, ask all students to write the required formula on a mini-whiteboard before starting the problem. Wait for all students to write something, or have a guess if they can’t remember.
• Provide students with a formula sheet to stick in the front of their exercise books so they’re not rifling through pages and pages to find the correct information.
• Get students to Google the formula they need (depending on your school’s mobile device policy) – and have a discussion about reliable sources of information!
• Make sets of flashcards with key formulae and get students to practise in pairs in the run-up to exams.

3. Include plenty of deliberate skills practise using formulae

One of the best ways to memorise a fact or formula is to use it frequently. Give students the opportunity to frequently practise previously-learned skills, particularly AO1-type recall questions, including plenty requiring applications of formulae.

4. Use units within a problem to derive compound measure formulae

When calculating speed, density and pressure, the units provided in the question are a great reminder of the formula to use.

Here we can see the density is given in g/cm³. Get students to think about what each of these units measure – grams is mass, and cm³ is volume, so we have the density is grams / cm³, or mass / volume.

5. Teach mnemonic and memory strategies for memorising formulae

Mnemonics can be a fantastic way of remembering key maths formulae – but ensure these don’t replace the underlying principles of understanding.

It may be useful to leave introduction of mnemonics and other memory tricks to Year 11, so that the mathematics takes precedence in the earlier years. We’ve all seen students happily write SOH CAH TOA on the top of an exam question and then not have a clue on how to proceed further.

Here are a few that my students have found useful:

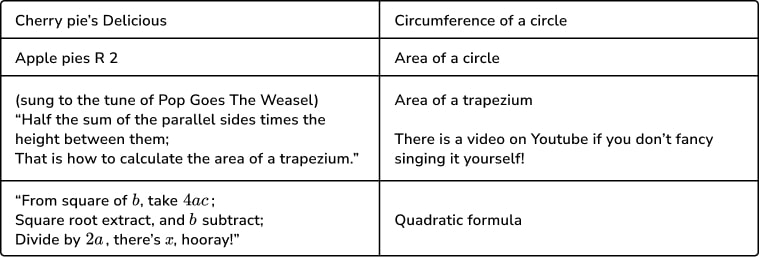
You can also get students to make up their own mnemonics or memory aides.

Strategies for identifying which formula to use

Students struggle massively with this one – they know the formulae, but they get to an exam question and can’t work out how to start. Here are a few tips:

1. Make sure they’ve read the question carefully

Quite a simple one to start off with: get them in the habit of making sure they haven’t missed anything, particularly key formulae that may be given as part of the question! It can sometimes be easy to overlook these.

2. Check for conceptual understanding

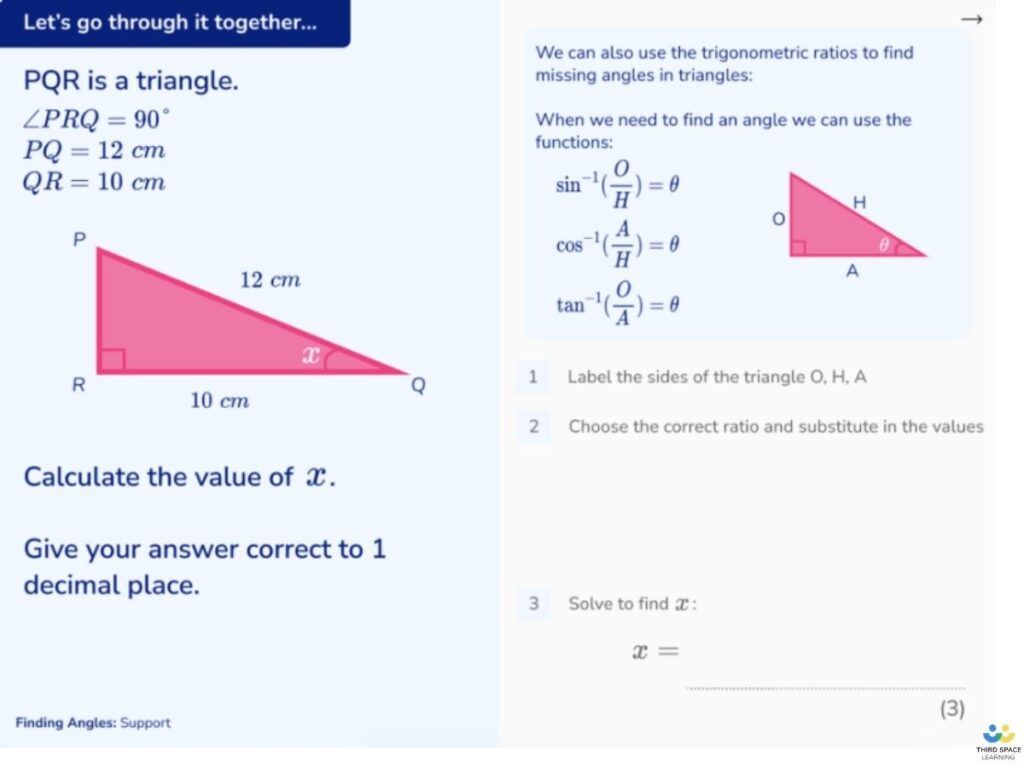
If a student is unable to identify which formula to apply in a procedural problem, this is likely to be symptomatic of a lack of conceptual understanding. 

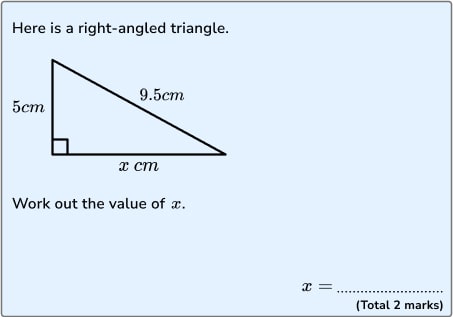
For example, if a student can’t identify that the problem above requires use of Pythagoras’ theorem, it is likely that there are issues with understanding that Pythagoras’ theorem relates to the three side lengths of right angled triangles – here I’d probably look at reteaching elements of Pythagoras’ theorem, particularly focusing on a couple of key ideas: 

• It relates to right-angled triangles;
• It concerns properties about the side lengths of the triangle.

Use these pythagoras theorem questions to help you.

3. Model your thinking when solving multi-step problems

With unfamiliar problems, or problems requiring applications of multiple related concepts, students can really struggle to find a way in, and therefore don’t attempt anything at all.

When modelling examples or solutions to exam questions, it’s really useful to show students your thought process, explaining how the question can be broken down into bits, almost like mini-questions:

It can be helpful for students to attempt shadow questions – the same style of question with different numerical values, or a small tweak. They then attempt to replicate your path through the solution.

You can also use a ratio table to model working for this problem. 

4. Deliberate practise of topic identification

This is really useful when working on past GCSE maths papers (usually in Year 11). This can be done as a stand-alone exercise on reduced-size copies of exam papers, or annotated on practice papers when students attempt these for homework.

Go through the paper question by question, and ask students to identify what GCSE maths topics they think might be needed for each question without doing any working out. You can then have a really valuable discussion about clues that you might see in questions, or strategies that you could try first.

This is also a good way of encouraging students to work independently on their revision – if the topic has been identified and they still don’t know how to begin the problem, they can then use independent learning resources to review that topic before attempting the exam problems.

GCSE maths formula sheets for each exam board

Edexcel : Need to Know Formulae A5 sheet

AQA : Mathematical Formulae

OCR : Print and Stick Formula Sheets